Математика - это искусство, а искусство - это математика

Цель работы:

Моя работа посвящена тому, чтобы показать «неразрывное» понятие между математикой и искусством; рассказать о современниках, их достижениях и показать работы в современном искусстве.

Общие темы в математическом искусстве

Многогранники

Тесселляции

Невозможные фигуры

Лента Мебиуса

Фрактал

Тесселляции

Тесселляции, известные также как покрытие плоскости плитками (tiling), являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов.

Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму.

Существует всего три многоугольника, пригодные для использования в правильных тесселляциях.

Это - правильный треугольник, квадрат и правильный шестиугольник.

Математика – это искусство, а искусство – это математика

Автор Голубева Н. Б.

Преподаватель математики

ГБОУ НПО ПЛ №114 МО

Цель работы : Моя работа посвящена тому, чтобы показать «неразрывное» понятие между математикой и искусством; рассказать о современниках, их достижениях и показать работы в современном искусстве.

Общие темы в математическом искусстве

• Многогранники
• Тесселляции
• Невозможные фигуры
• Лента Мебиуса
• Фрактал

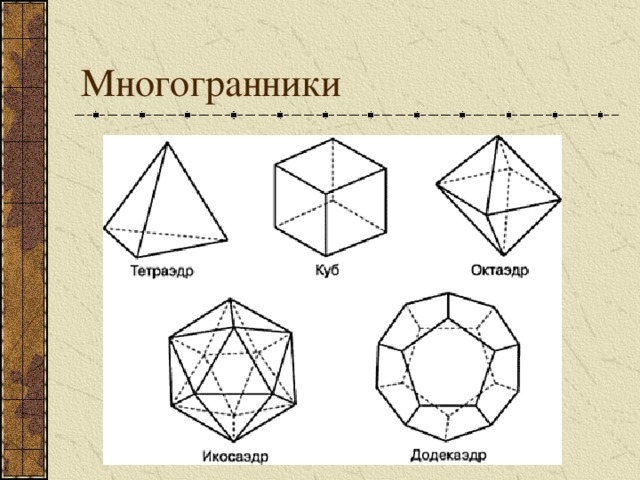
Многогранники

Тесселляции

Тесселляции, известные также как покрытие плоскости плитками (tiling), являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник.

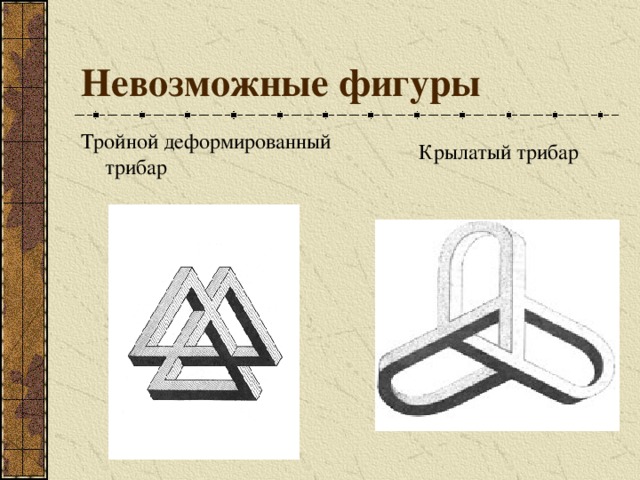
Невозможные фигуры

Тройной деформированный трибар

Крылатый трибар

Лента Мебиуса

Лента Мебиуса - это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один концов полоски, а затем склеив оба конца друг с другом.

Она была открыта независимо одновременно двумя математиками из Германии Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году.

Искаженные и необычные перспективы

Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область - анаморфное искусство. Слово анаморфный (anamorthic) сформировано из двух греческих слов "ana" (снова) и morthe (форма). К анаморфным относятся изображения настолько сильно искаженные, что разобрать их без специального зеркала бывает невозможно. Такое зеркало иногда называют анаморфоскопом. Если смотреть в анаморфоскоп, то изображение "формируется снова" в узнаваемую картину .

Фрактал

Фрактал - это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей.

Мауриц Эшер

• Мауриц Корнелис Эшер (нидерл. Maurits Cornelis Escher; 17 июня 1898, Леуварден, Нидерланды — 27 марта 1972, Хилверсюм, Нидерланды) — нидерландский художник-график. Известен, прежде всего, своими концептуальными литографиями, гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трёхмерных объектов, самый яркий представитель имп-арта.

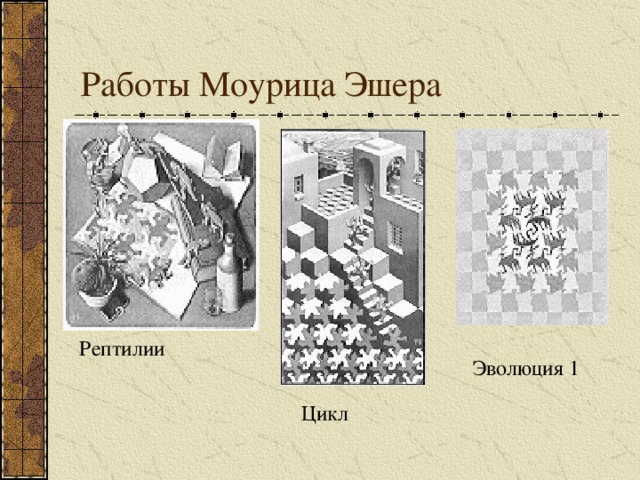
Работы Моурица Эшера

Рептилии

Эволюция 1

Цикл

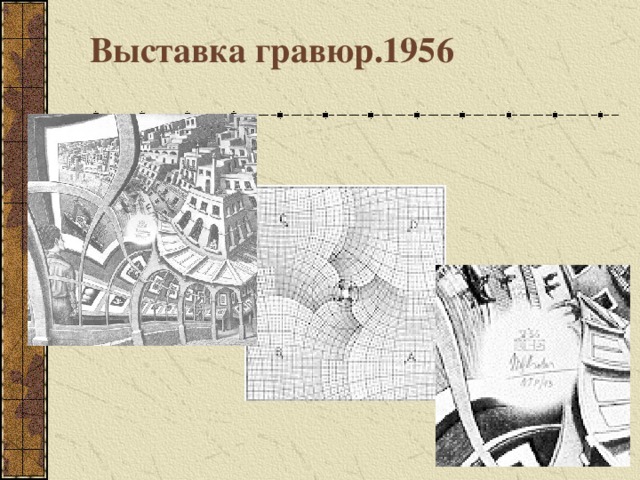
Выставка гравюр.1956

Порядок и хаос (1950)

Звездный додекаэдр, расположенный в центре, как мыльным пузырем, накрыт прозрачной сферой. В этом символе порядка и красоты отражается хаос в виде различного собрания ненужных, разбитых и сплющенных предметов. Эта картина напоминает нам о беззащитности нашей земли, вселенной, экологических и индустриальных катастрофах.

Звезды (1948)

Одиночные, двойные и тройные геометрические правильные тела парят в пространстве. В центре – конструкции из трех правильных полых октаэдров. Обитателями этой структуры избраны два хамелеона. Поскольку они способны уцепиться своими длинными ногами и хвостами за перекладины клетки, которая бешено вращаясь, мчится в пространстве.

Мандельброт Бенуа

• 20 ноября 1924- 14 октября 2010— французский и американский математик, создатель фрактальной геометрии.
• Лауреат премии Вольфа по физике.
• Почётный преподаватель Йельского Университета
• Баттельский член Тихоокеанской северо-западной национальной лаборатории.

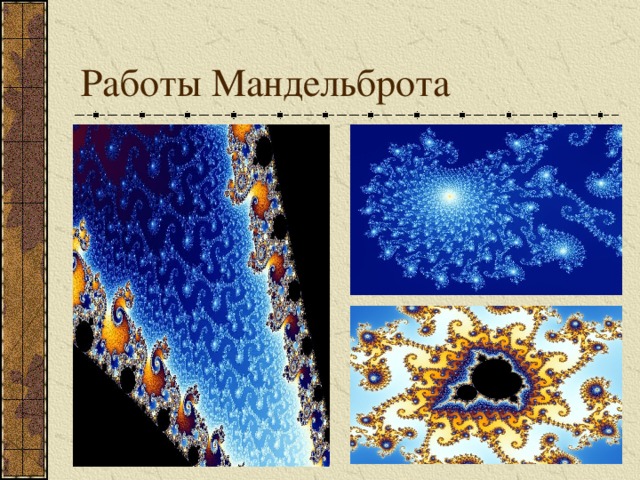
Работы Мандельброта

Роберт Фатауэр

«Кристалл Фатауэра» строится из 13 повторений фрактального узора — кубы, помещенные на кубы, помещенные на кубы.

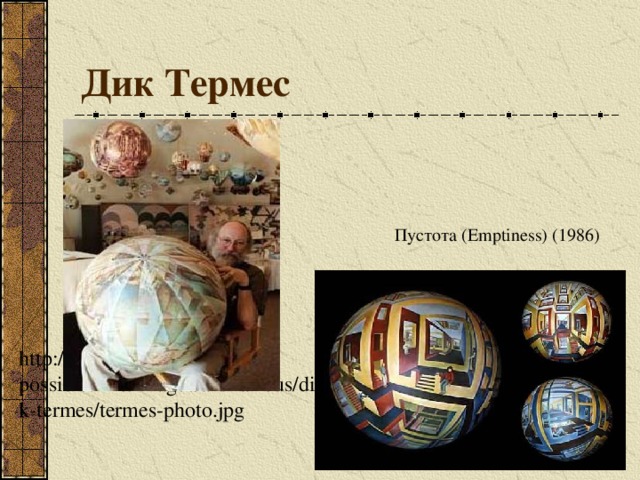
Дик Термес

Пустота (Emptiness) (1986)

http://im-possible.info/images/art/various/dick-termes/termes-photo.jpg

Клетка для человека (1978).

Это разукрашенная сфера, в процессе создания которой использовалась шеститочечная перспектива. На ней изображения геометрическая структура в виде сетки, сквозь которую виден ландшафт. Три ветки проникают внутрь клетки, а также по ней ползают рептилии. В то время как одни изучают мир, другие обнаруживают себя, находящимися в клетке.

Братья Мартин и Эрик Демэйны

Один из их текущих проектов состоит в том, чтобы изучить изогнутые сгибы в оригами, которое означают и понимание его математических свойств и понимание его артистического потенциала. Демэйны в настоящее время работают с кривыми складками: взятие круга, включение малого круга в центре, и сворачивание в чередовании сгибов вдоль концентрических кругов.

Последние вышедшие работы братьев Демэйнов (2011-2012)

Вращающиеся квадраты

«Awake»

«Circling Squares»

Пробуждение

Зеленый водопад

«Swim»

«Green Waterfall»

Плавающий

Дэвид Холлистер "Семь птиц". На этой картине изображены семь птиц, две из которых изображены в негативе на фоне ландшафта города Ахо в Аризоне. Последовательно уменьшающиеся фигуры птиц совмещаются друг с другом в виде фрактальной тесселляции. Хвостовые перья каждой птицы являются разделяют конструкцию напополам, отсекая примерно треть расстояния между кончиками крыльев. Каждая меньшая птица в свою очередь делит свою область аналогичным образом. Если этот процесс продолжать до бесконечности, получится набор точек, известный как множество Кантора или Канторова пыль.

Орос Иштван

Венгерский художник-график и художник-мультипликатор. Наиболее известен работами в области оптического искусства, использующими различные оптические иллюзии и изображающими невозможные фигуры, рисунки с двойным смыслом и анаморфозы.

Орос Иштван " Перекрестки" (1999). Репродукция гравюры по металлу. На картине изображены мосты, которые не могут существовать в трехмерном пространстве. Например, есть отражения в воде, которые не могут быть исходными мостами.

Использованные Интернет ресурсы

Слайд 4

http://trinitas.ru/rus/doc/0202/010a/pic/0057/0057-06.gif

Слайд 6

Тройной деформированный трибар

http://www.portalus.ru/modules/culture/special/imp/imp-world-r.narod.ru/articles/unruch/page13.gif

Крылатый трибар

http://library.by/portalus/modules/culture/special/imp/imp-world-r.narod.ru/articles/unruch/page17.gif

Слайд 7 Лента Мебиуса

http://copypast.ru/uploads/posts/thumbs/1344023364_800pxmgbius_strip.jpg

Слайд 9 Фрактал

http://upload.wikimedia.org/wikipedia/commons/thumb/2/21/Mandel_zoom_00_mandelbrot_set.jpg/250px-Mandel_zoom_00_mandelbrot_set.jpg

Слайд 10 Портреты Эшера

http://www.freakingnews.com/pictures/43000/Escher-Portrait---43408.jpg

http://upload.wikimedia.org/wikipedia/en/4/43/EscherSelf1929.jpg

Слайд 11

Рептилии

http://im-possible.info/images/articles/escher_math/reptiles_small.gif

цикл

http://im-possible.info/images/articles/escher_math/cycles_small.gif

Эволюция 1

http://im-possible.info/images/articles/escher_math/development1_small.gif

Слайд 12 Выставка гравюр

http://www.videomax.ru/forum/uploads/12924/printgallery.jpg

http://im-possible.info/images/articles/escher_math/print_gallery_schema.gif

http://im-possible.info/images/articles/escher_math/print_gallery_sign.gif

Слайд 13

Порядок и хаос

http://im-possible.info/images/articles/escher_math/order_and_chaos_small.gif

Звезды

http://im-possible.info/images/articles/escher_math/stars_small.gif

Слайд 14 Мандельброт Бенуа

http://publikashka.com/_pu/1/32912424.jpg

Слайд 15 Работы Мандельброта

http://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Mandel_zoom_09_satellite_head_and_shoulder.jpg/800px-Mandel_zoom_09_satellite_head_and_shoulder.jpg

http://www.marywood.edu/dotAsset/281930.jpg

http://im2-tub-ru.yandex.net/i?id=28221112-49-73&n=21

Слайд 16

Портрет Роберта Фатауэр http://1-ps.googleusercontent.com/h/www.incredibleart.org/lessons/middle/images/225x276xfathauer.jpg.pagespeed.ic.SYU6O4ssqC.webp

Кристалл Фатауэра»

http://www.diggreader.ru/wp-content/img/08march/math/3.jpg

Слайд 17

Дик Термес http://im-possible.info/images/art/various/dick-termes/termes-photo.jpg

Пустота http://im-possible.info/images/art/various/dick-termes/emptiness.jpg

Слайд 18

Клетка для человека http://im-possible.info/images/articles/vis_math_art/fig5.jpg

Слайд 19

Братья Мартин и Эрик Демэйны http://en.academic.ru/pictures/enwiki/69/Erik_Demaine_et_al_2005_cropped.jpg

Слайд 20

Работа Дейменов http://content.foto.mail.ru/inbox/nadya53/135/i-139.jpg

Слайд 21

Пробуждение http://erikdemaine.org/curved/Simons/thumbs/C0194-009_small.jpg

Зеленый водопад http://erikdemaine.org/curved/FullerCraft/0191a_medium.jpg

Вращающиеся квадраты http://im0-tub-ru.yandex.net/i?id=213283887-51-73&n=21

Плавающий http://erikdemaine.org/curved/Simons/thumbs/B0195-007_small.jpg

Слайд 22

Дэвид Холлистер «Семь птиц» http://im-possible.info/images/art/various/hop_david/seven_birds.jpg

Слайд 23

Орос Иштван http://lifeglobe.net/x/entry/1719/1-16.jpg

Слайд 24

Орос Иштван « Перекрестки» http://im-possible.info/images/art/orosz/large/crossroads_.jpg

Список литературы

• Волошинов А.В. Математика и искусство. – М., 1992.
• Шарыгин И.Ф., Ерганжиева Л.Н. // Наглядная геометрия. – М., «Дрофа», 1998.
• Очинский В.В. Система музыкальных звуков как функция отношений золотой пропорции. Циклические процессы в природе и обществе//Математика и искусство. – , 1994, № 3.С.161 – 167.
• Перевод Влада Алексеева
• M. C. Escher - His Life and Complete Graphic Work, by F.H. Bool, J.R. Kist, J.L. Locher, and F. Wierda (Harry N. Abrams, New York, 1982).
• The Magic Mirror of M. C. Escher, by Bruno Ernst (Ballantine Books, New York, 1976).
• Visions of Symmetry - Notebooks, Periodic Drawings, and Related Works of M. C. Escher, by Doris Schattschneider (W.H. Freeman and Co., New York, 1990).
• "Fractals and an Art for the Sake of Science," Benoit B. Madelbrot, in The Visual Mind, ed. by Michele Emmer (MIT Press, Cambridge, 1993).
• Математика Приложение к газете «Первое сентября» №7-96. Рисунки Эшера.
• Кордемский Б.А. Великие жизни в математике, М.: Просвещение,1995.
• Интернет – ресурсы:
• Impossible Word [Электронный ресурс]: - Режим доступа: http://im-possible.info/russian/articles/vis_math_art/ , свободный.
• Мауриц Корнелис Эшер [Электронный ресурс]: - Режим доступа: http://mcesher.ru/ , свободный.
• Фракталы [Электронный ресурс]: - Режим доступа: http://rusproject.narod.ru/article/fractals.htm , свободный.
• Публикашка [Электронный ресурс]: - Режим доступа: http://publikashka.com/publ/zaumki/b_mandelbrot_fraktalnaja_geometrija_prirody/1-1-0-128 , свободный.
• Эрик Деймен [Электронный ресурс]: - Режим доступа: http://erikdemaine.org/ , свободный.
• Trendclub [Электронный ресурс]: - Режим доступа: http://trendclub.ru/3886 , свободный.