Получите свидетельство
Вход
Тема урока:
Площадь круга и кругового сектора.
Вспомним, чему равно отношение длины окружности к ее диаметру .
Лабораторная работа:
- С помощью нити измерьте длину окружности.
- Измерьте линейкой диаметр окружности.
- Найдите отношение С : D
- Занесите полученные данные в таблицу.
- Сделайте вывод.
Площадь круга.
Часть плоскости,
ограниченная окружностью.
Какая геометрическая фигура
называется кругом?
Площадь круга.
S = πR 2
- А 1 А 2 …А п – правильный п – угольник
с площадью S n.
- Окр. (О; R) – окружность с площадью
S, описанная около многоугольника.
. О
А 2
- Окр. (О; r) – окружность с площадью S 2 , вписанная в многоугольник.
R
r
4) Сравните S, S 2 и S n .
S 2 n
А п
А 1
5) n → ∞
6) Т.к. r → R, то P n → 2πR.
Что такое сектор?
Это тоже сектор
Это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром окружности.
Это сектор
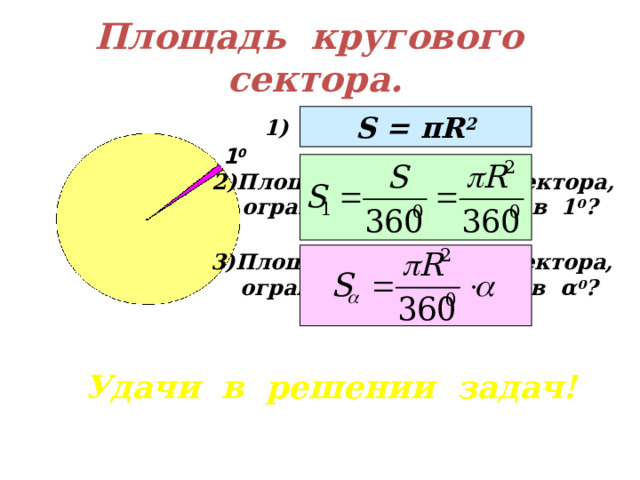
Площадь кругового сектора.
S = πR 2
1) Площадь круга?
1 0
- Площадь кругового сектора,
ограниченного дугой в 1 0 ?
- Площадь кругового сектора,
ограниченного дугой в α 0 ?
Удачи в решении задач!
Задачи:
№ 1
Диаметр основания
Царь-колокола, находящегося
в московском Кремле, равен 6,6 м. Найдите площадь основания колокола.
№ 2.
Длина окружности
цирковой арены равна 41 м. Найдите диаметр
и площадь арены.
S ≈ 34,2 м 2
Задача № 3:
Из круга, радиус которого 10 см,
вырезан сектор с дугой в 60 0 .
Найдите площадь оставшейся
части круга.
S кр
10
Решение: 1 вариант
60 0
S 2 - ?
S 1
3) S 2 = 314 – 52,3 = 261,7см 2
2 вариант
Устный тест:
- Установите, истины или ложны следующие высказывания:
а) Площадь круга равна произведению квадрата
его радиуса на π.
б) Площадь круга можно вычислить по формуле
, где D – диаметр круга.
в) Площадь круга радиуса 10 равна 10 π.
г) Площадь кругового сектора, ограниченного дугой
в 90 0 , вычисляется по формуле
Устный тест:
- Закончите утверждение:
- Если диаметр круга увеличить в 4 раза, то
площадь круга увеличится в … раз.
16
- Если радиус круга равен 6 см, то площадь его
кругового сектора вычисляется по формуле:
3) Площадь вписанного в окружность квадрата
равна 16 см 2 . Площадь круга, ограниченного
данной окружностью, равна …
8 π
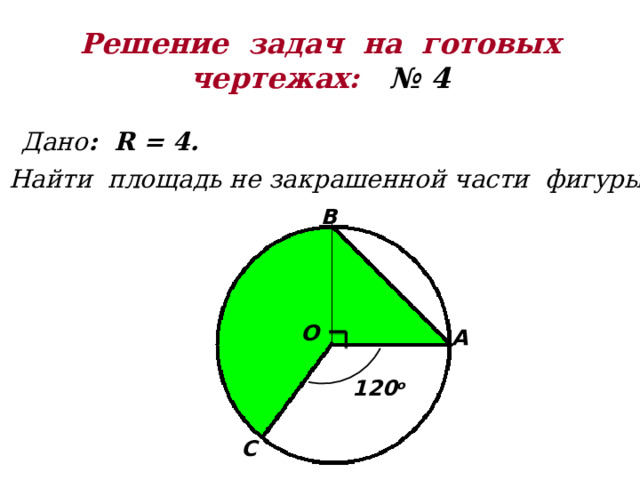
Решение задач на готовых чертежах: № 4
Дано : R = 4.
Найти площадь не закрашенной части фигуры .
В
О
А
120 о
С
План решения:
1. Вычислить площадь круга.
2. Вычислить площадь сектора.
3. Вычислить площадь треугольника.
4. Вычислить площадь не закрашенной части фигуры.
4. S ф ≈ 16π – 16 – 8 = 26
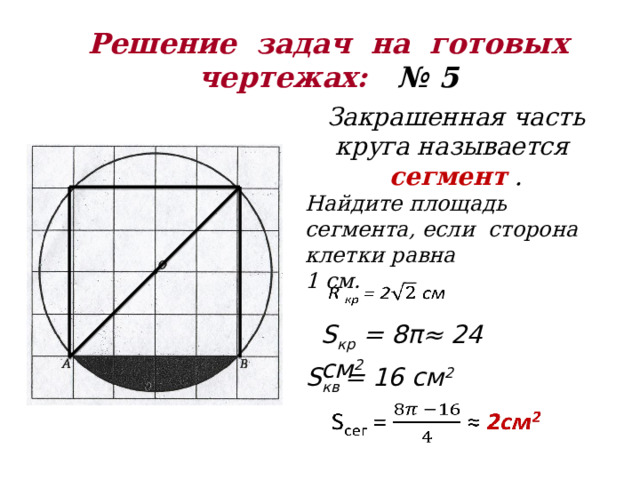
Решение задач на готовых чертежах: № 5
Закрашенная часть круга называется
сегмент .
Найдите площадь сегмента, если сторона клетки равна
1 см.
S кр = 8π≈ 24 см 2
S кв = 16 см 2
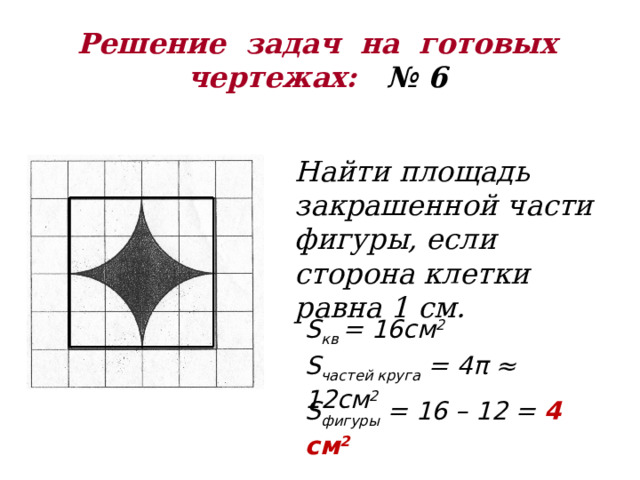
Решение задач на готовых чертежах: № 6
Найти площадь закрашенной части фигуры, если сторона клетки равна 1 см.
S кв = 16см 2
S частей круга = 4π ≈ 12см 2
S фигуры = 16 – 12 = 4 см 2
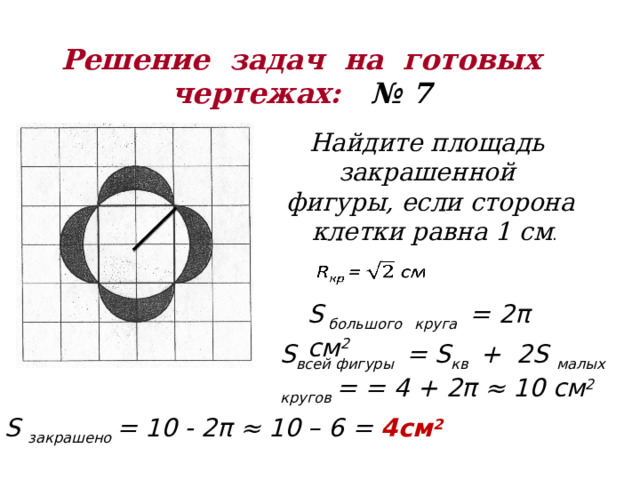
Решение задач на готовых чертежах: № 7
Найдите площадь
закрашенной
фигуры, если сторона
клетки равна 1 см .
S большого круга = 2π см 2
S всей фигуры = S кв + 2S малых кругов = = 4 + 2π ≈ 10 см 2
S закрашено = 10 - 2π ≈ 10 – 6 = 4см 2
Подводя итог урока, ответьте на вопросы:
- Что нового узнали?
- Чему научились на уроке?
- Где могут пригодиться полученные знания и умения?
Домашнее задание:
Пп. 111, 112
№№ 1120; 1124; 1126.
Творческое задание :
написать реферат (презентацию)
или выступить с сообщением
«Неизвестное об известном: число π»
Комментарий к д/з:
№ 1124
R 1 → S 1
Площадь кольца
2
R 2 → S 2
1
? ? ? …
4
3
R 3 → S 3
… … … …
№ 1126
?
60 0
Урок окончен .
Спасибо за внимание.
Площадь круга и кругового сектора. (670.12 KB)
0
1087
140
Нравится
0
