«Приемы быстрого счета на уроках математики»
ВВЕДЕНИЕ
«Ну-ка, в сторону карандаши!
Ни костяшек, ни ручек, ни мела!
Устный счет мы творим - это дело!
Только сила ума и души.
Числа сходятся где-то во тьме,
И глаза начинают светиться.
А кругом только умные лица,
Устный счет мы считаем в уме»
Эффективная педагогическая технология – это не просто использование технических средств обучения или компьютеров, «это выявление принципов и разработка приемов оптимизации образовательного процесса путем анализа факторов, повышающих образовательную эффективность путем конструирования и применения приемов и материалов, а также посредством оценки применяемых методов»
Одно из условий успешного обучения математике - хорошо развитые у учащихся навыки устного счета. Именно в пятых-седьмых классах закладываются основы обучения математике, поэтому с первых уроков учителю необходимо обращать особое внимание на устный счет. Начальные уроки можно посвящать обучению приемам быстрого счета, которые помогают ускорять не какие-нибудь сложные вычисления, а самые обычные числовые выкладки, с которыми постоянно приходится иметь дело на уроках.
В наше время существует мнение, что человеку не надо знать приемы быстрых вычислений, что для этого существуют компьютеры. Однако польза устных вычислений огромна.
1) Применяя законы арифметических действий к устным вычислениям, можно повторить, закрепить, усвоить их не механически, а сознательно.
2) При устных вычислениях развиваются внимание, сосредоточенность, смекалка, самостоятельность.
3) Устный счет содействует тренировке памяти.
4) В то время как письменные вычисления однообразны и шаблонны, в устных вычислениях нет готового шаблона и приемы вычислений разнообразны, что способствует развитию чрезвычайно полезных качеств человека.
Во все времена математика была и остается одним из основных предметов в школе, потому что математические знания необходимы всем людям. Не каждый школьник, обучаясь в школе, знает, какую профессию он выберет в будущем, но каждый понимает, что математика необходима для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. Кроме того, всем школьникам необходимо сдавать экзамены в 9-м классе и в 11-м классе, а для этого, обучаясь с 1-го класса, необходимо качественно осваивать математику и прежде всего, нужно научиться считать.
Обучение математике – это искусство, направленное вовсе не на весь класс одновременно, а на каждого ученика в отдельности. Урок – как музыкальное произведение, рождается со звонком и умирает со звонком, пролетает для тридцати пар глаз одновременно, но в душе и в уме каждого ученика оставляет свой собственный след, рождает тропинку, по которой еще предстоит продираться через дебри и овраги к пониманию, к истине. Но не все дети одинаково трудолюбивы. Поэтому очень важным мы считаем найти путь к пониманию и сердцу ребенка.
Уроки с применением современных образовательных технологий, отличаются от уроков в традиционном обучении. Ученики не сидят пассивно, слушая учителя, а становятся главными действующими лицами урока. Они думают и делятся рассуждениями друг с другом. Средства технологии позволяют работать с информацией в любой области знания, а это значит, что ознакомление с ней можно организовать на любом предметном материале. Сознание детей уже подготовлено к восприятию информационного мира, они с легкостью осваивают информационные и коммуникационные технологии, многие из них способны самостоятельно обучаться.
Сейчас, на этапе стремительного развития информатики и вычислительной техники, современные школьники не хотят утруждать себя счетом в уме. Поэтому мы решили показать не только то, что сам процесс выполнения действия может быть важным, но и интересным занятием.
Актуальность исследования состоит в том, что в наше время все чаще на помощь ученикам приходят калькуляторы, и все большее количество учеников не может считать устно;
устные приемы на уроках математики развивают логическое мышление, память, гибкость ума, приучают человека к точности;
в процессе обучения развиваются умения и навыки быстрого счёта, результат выполнения действий может быть не только полезным, но и интересным занятием.
Данная тема актуальна, так как выполнять быстро, рационально, без использования калькулятора устные вычисления, необходимо при подготовке к ЕНТ. Математика является одной из важнейших наук на земле, и именно с ней человек встречается каждый день в своей жизни. Поэтому мы формируем у детей вычислительные навыки, используя различные виды устных упражнений.
Цель:
изучить приемы быстрого счета,
показать необходимость их применения для упрощения вычислений
доказать результативность использования различных видов устного счета для повышения познавательного интереса к урокам математики.
развивать логическое и творческое мышление
В соответствии с поставленной целью были определены задачи:
Изучить теорию данного вопроса в психолого-педагогической и методической литературе.
Изучить приемы быстрого счета, которые можно использовать, упрощая вычисления.
Подготовить и провести различные виды устных упражнений для повышения познавательного интереса к урокам математики
Исследовать, применяют ли школьники приемы быстрого счета.
Сделать выводы, по использованию данных видов устных упражнений.
Составить памятку для учащихся 5-6 классов для применения приемов быстрого счета.
Гипотеза исследования:
применение приемов быстрого счета, облегчает вычисления
повышается вычислительная культура учащихся
быстрота решения практических задачи.
Объект исследования: специально организованный педагогический процесс,
в плане поиска эффективных методов обучения (в частности устных упражнений).
Предмет исследования: влияние различных видов устного счета на повышение познавательного интереса к урокам математики у детей.
При выполнении работы были использованы следующие приемы и методы: опрос (анкетирование), анализ (статистическая обработка данных), работа с источниками информации, практическая работа, наблюдения.
Данная работа относится к прикладным исследованиям, т.к. в ней показывается роль применения приемов быстрого счета для практической деятельности.
При работе над проектом мы пользовались следующими методами:
поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;
практический метод выполнения вычислений с применением нестандартных алгоритмов счета;
анализ полученных в ходе исследования данных.
Новизна исследования
Комбинирование различных форм и методов обучения для повышения эффективности деятельности на уроке
Достижение поставленной цели наиболее рациональными и экономичными путями
Создание условий для активной познавательной деятельности обучающихся
Применение информационных технологий на уроках математики и информатики
«Если ученик в школе не научился сам ничего творить, то и в жизни он всегда будет только подражать, копировать, т.к. мало таких, которые бы, научившись копировать, умели сделать самостоятельное приложение этих сведений» - писал Л.Н.Толстой.
Поэтому должна продумываться каждая деталь урока, чтобы все заставляло учащихся мыслить.
За простыми действиями сложения, вычитания, умножения и деления скрываются тайны истории математики. Случайно услышанные слова «умножение решеткой», «шахматным способом» заинтриговали. Захотелось узнать эти и другие способы вычислений, а также сравнить их с сегодняшними.
Умеете ли вы считать? Вопрос, пожалуй, даже обидный для человека старше трехлетнего возраста. Кто не умеет считать? Каждый ответит, что для этого, особого искусства не требуется. И будет прав. Но вопрос – как считать? Можно считать на калькуляторе, можно считать столбиком в тетради, а можно считать устно, используя приемы быстрого счета. Нам захотелось выяснить, а знают ли учащиеся приемы быстрого счета, если нет, то помочь им освоить эти приемы, с этой целью составить для них памятку с приемами быстрого счета.
Для того чтобы выяснить, знают ли современные школьники другие способы выполнения арифметических действий, кроме умножения, сложения, вычитания столбиком и деления «уголком» и хотели бы узнать новые способы, был проведен тестовый опрос.
Для начала, мы провели анкетирование в 6-х классах нашей школы. Задавали ребятам простые вопросы. Зачем вообще нужно уметь считать? При изучении каких школьных предметов требуется правильный счет? Знают ли они приемы быстрого счета? Хотели бы научиться быстро считать устно? (Приложение I).
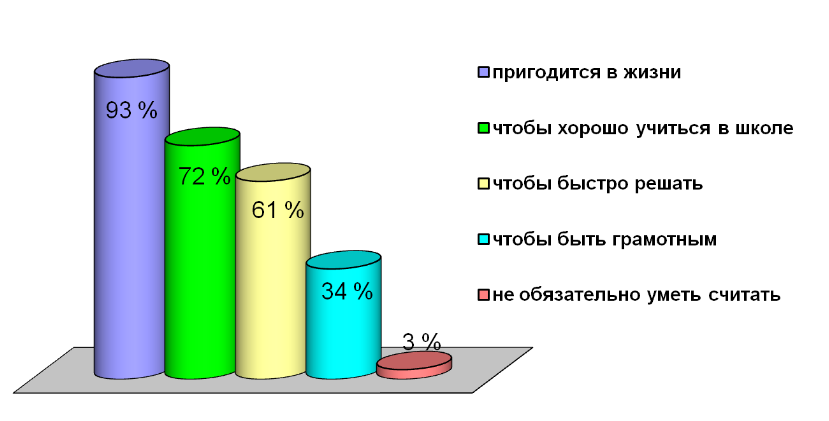
В опросе приняли участие 61 человек. Проанализировав результаты, мы сделали выводы, что большинство учеников считает, что умение считать пригодится в жизни и необходимо в школе, особенно при изучении математики, физики, химии, информатики и технологии. Приемы быстрого счета знают несколько учеников и почти все хотели бы научиться быстро считать. (Результаты анкетирования отражены в диаграммах) (Приложение II).
Проведя статистическую обработку данных, мы сделали выводы, что не все учащиеся знают приемы быстрого счета, поэтому необходимо сделать для учеников 5-6-х классов памятки с приемами быстрого счета, чтобы использовать их при выполнении вычислений.
Результаты анкетирования.
Сводная таблица анкетирования:
| Вопрос | 5, 6 классы |
| да | нет | не знаю |
| Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку? | 53 | 7 | 1 |
| Умеете ли вы умножать, складывать, вычитать числа столбиком, делить «уголком»? | 55 | 6 | _ |
| Знаете ли вы другие способы выполнения арифметических действий? | 24 | 37 | _ |
| А хотели бы узнать? | 51 | 4 | 6 |
УСТНЫЙ СЧЕТ – ГИМНАСТИКА УМА 1.УМНОЖЕНИЕ НА ПАЛЬЦАХ
Движение пальца – это еще один из способов помочь памяти: с помощью пальцев рук запомнить таблицу умножения на 9. Положив обе руки рядом на стол, по порядку занумеруем пальцы обеих рук следующим образом: первый палец слева обозначим 1, второй за ним обозначим цифрой 2, затем 3, 4… до десятого пальца, который означает 10. Если надо умножить на 9 любое из первых девяти чисел, то для этого, не двигая рук со стола, надо приподнять вверх тот палец, номер которого означает число, на которое умножается девять; тогда число пальцев, лежащих налево от поднятого пальца, определяет число десятков, а число пальцев, лежащих справа от поднятого пальца, обозначает число единиц полученного произведения (убедитесь в этом самостоятельно).
Пример: 8 ∙ 9 = 72
Однако, он достаточно быстр и наиболее удобен.
2. РАЗЛИЧНЫЕ СПОСОБЫ УМНОЖЕНИЯ И ДЕЛЕНИЯ
Изучив литературу по данной теме, нами был сделан отбор, из множества приемов быстрого счета, мы выбрали приемы умножения и деления, которые просты в понимании и применении для любого ученика. Эти приемы мы и включил в памятку, которая будет полезна для учеников 5-6-х классов.
Умножение и деление числа на 4.
Чтобы умножить число на 4, нужно его дважды умножить на 2.
Например:
26·4=(26·2)·2=52·2=104;
417·4=(417·2)·2=834·2=1668.
Чтобы разделить число на 4, нужно его дважды разделить на 2.
Например:
324:4=(324:2):2=162:2=81.
Умножение и деление числа на 5.
Чтобы умножить число на 5, нужно его умножить на 10 и разделить на 2.
Например:
236·5=(236·10):2=2360:2=1180.
Чтобы разделить число на 5, нужно умножить 2 и разделить на 10, т.е. отделить запятой последнюю цифру.
Например:
236:5=(236·2):10=472:10=47,2.
Умножение числа на 1,5.
Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину.
Например: 34·1,5=34+17=51;
146·1,5=146+73=219.
Умножение числа на 9.
Чтобы умножить число на 9, нужно к нему приписать 0 и отнять исходное число. Например: 72·9=720-72=648.
Умножение на 25 числа, делящегося на 4.
Чтобы умножить на 25 число, делящееся на 4, нужно его разделить на 4 и получившееся число умножить на 100.
Например: 124·25=(124:4)·100=31·100=3100.
Умножение двузначного числа на 11
При умножении двузначного числа на 11, нужно между цифрой единиц и цифрой десятков вписать сумму этих цифр, причем, если сумма цифр больше 10, то единицу нужно прибавить к старшему разряду (первой цифре).
Например:
23·11=253, т.к. 2+3=5, поэтому между 2 и 3 ставим цифру 5;
57·11=627, т.к. 5+7=12, цифру 2 ставим между 5 и 7, а к 5 прибавляем 1, вместо 5 пишем 6.
«Краешки сложи, в серединку положи» - эти слова помогут легко запомнить данный способ умножения на 11.
Такой способ подходит только для умножения двузначных чисел.
Умножение двузначного числа на 101.
Для того, чтобы число умножить на 101, нужно приписать данное число к самому себе.
Например:34·101 = 3434.
Поясним, 34·101 = 34·100+34·1=3400+34=3434.
Возведение в квадрат двузначного числа, оканчивающегося на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25.
Например: 352=1225, т.е. 3·4=12 и к 12 приписываем 25, получаем 1225.
Возведение в квадрат двузначного числа, начинающегося на 5.
Для возведения в квадрат двузначного числа, начинающегося на пять, нужно прибавить к 25 вторую цифру числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0.
Например:
522= 2704, т.к. 25+2=28 и 22=04;
582= 3364, т.к. 25+8=33 и 82=64.
10) Умножение с помощью формул сокращенного умножения
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a-b)(a+b)=a2-b2
a2-b2= (a-b)(a+b)
Примеры:
88∙92 =(90-2)∙(90+2)=8100-4=8096
532=(50+3)2=2500+2∙50∙3+9=2809
39² - 36² = ( 39 – 36 ) ∙ ( 39 + 36 ) = 3 ∙ 75 = 3 ∙ 3 ∙ 25
11) Умножение чисел, у которых цифры десятков одинаковые, а сумма цифр единиц составляет 10
83∙87=8∙(8+1)∙100+3∙7=7200+21=7221 или (8∙9)(3∙7)=7221
204∙206=20∙(20+1)∙100+4∙6=42024 или (20∙21)(4∙6)=42024
Правило 1: число десятков первого числа на число десятков второго числа, увеличенного на 1, помножим на 100. Перемножим вторые цифры данных чисел. Результаты сложить.
12) Приемы запоминания тригонометрических формул
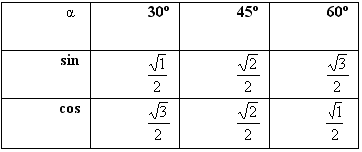
а) Табличные значения тригонометрических функций. Для запоминания значений синуса и косинуса для углов в 30º, 45º и 60º мы предлагаем своим ученикам притчу.
– Пошли три дамы гулять. Первая дама, вторая дама и третья дама. И неожиданно пошел дождь. Все дамы открыли зонтики, и одели по паре калош. Прогулка была закончена, и дамы вернулись домой. Первая дама, вторая дама и третья дама пошли домой. (Сначала, в таблице, во второй строке по порядку указываются номера дам. За тем изображают корни – “зонтики”, и “надевают калоши” – в знаменателях пишут 2).
Чтобы указать значения тангенса и котангенса тех же углов достаточно вспомнить основные тригонометрические тождества, т.е 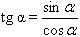 , а котангенс взаимно обратная функция для тангенса.
, а котангенс взаимно обратная функция для тангенса.
б) Формулы приведения
Тригонометрические функции углов вида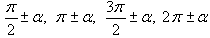 могут быть выражены через функции угла α с помощью формул, которые называют формулами приведения. Но запоминать эти формулы не обязательно. Для преобразования таких выражений достаточно знать знаки тригонометрических функций по четвертям и еще одну притчу.
могут быть выражены через функции угла α с помощью формул, которые называют формулами приведения. Но запоминать эти формулы не обязательно. Для преобразования таких выражений достаточно знать знаки тригонометрических функций по четвертям и еще одну притчу.
– Жил забывчивый математик, и каждый раз преобразовывая тригонометрические функции углов вида 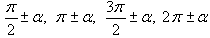 , он спрашивал у своей лошади, жующей за окном сено, надо менять функцию на конфункцию или нет. А лошадь кивала головой по той оси, на которой располагался угол
, он спрашивал у своей лошади, жующей за окном сено, надо менять функцию на конфункцию или нет. А лошадь кивала головой по той оси, на которой располагался угол 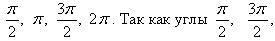 являющиеся границами первой и третьей четвертей соответственно, лежат на оси Оу, то лошадь кивком головы подтверждала смену функции на конфункцию. А для углов
являющиеся границами первой и третьей четвертей соответственно, лежат на оси Оу, то лошадь кивком головы подтверждала смену функции на конфункцию. А для углов 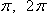 наоборот отрицала. Математику оставалось лишь записывать ответ, указывая знак данной функции.
наоборот отрицала. Математику оставалось лишь записывать ответ, указывая знак данной функции.
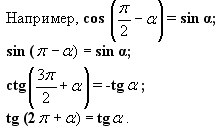
в) Формулы сложения – это та, группа формул которую нужно знать наизусть. Но для их запоминания можно тоже воспользоваться ассоциативным приемом. У косинуса функции одноименные, а у синуса разноименные. Не все в нашей жизни бывает “гладко” за белой полосой идет черная, и наоборот. Так и у наших функций, если функции идут одноименные, то знаки не совпадают, а если разноименные, то совпадают.
cos (α β ) = cos α cos β + sin α sin β;
cos (α + β ) = cos α cos β – sin α sin β;
sin (α + β) = sin α cos β + cos α sin β;
sin (α – β) = sin α cos β – cos α sin β.
3. ИГРЫ
Отгадывание полученного числа.
Задумайте какое-нибудь число. Прибавьте к нему 11; умножьте полученную сумму на 2; от этого произведения отнимите 20; умножьте полученную разность на 5 и от нового произведения отнимите число, в 10 раз больше задуманного вами числа. Я отгадываю: вы получили 10. Верно?
Задумайте число. Утрой его. Вычти из полученного 1. Полученное умножьте на 5. К полученному прибавьте 20. Разделите полученное на 15. Из полученного результата вычтите задуманное. У вас получилось 1.
Задумайте число. Умножьте его на 6. Вычтите 3. Умножьте на 2. Прибавьте 26. Вычтите удвоенное задуманное. Разделите на 10. Вычтите задуманное. У вас получилось 2.
Задумайте число. Утройте его. Вычтите 2. Умножьте на 5. Прибавьте 5. Разделите на 5. Прибавьте 1. Разделите на задуманное. У вас получилось 3.
Задумайте число, удвойте его. Прибавьте 3. Умножьте на 4. Вычтите 12. Разделите на задуманное. У вас получилось 8.
Угадывание задуманных чисел.
Предложите своим друзьям задумать любые числа. Пусть каждый прибавит к своему задуманному числу 5.
Полученную сумму пусть умножит на 3.
От произведения пусть отнимет 7.
Из полученного результата пусть вычтет ещё 8.
Листок с окончательным результатом пусть каждый отдаст вам. Глядя на листок, вы тут же говорите каждому, какое число он задумал.
(Чтобы угадать задуманное число, результат, написанный на бумажке или сказанный вам устно, разделить на 3).
ЗАКЛЮЧЕНИЕ
Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, «экономическую ситуацию» в стране, погоду на «завтра», описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в IV веке д.н.э. – Пифагора– «Всё есть число!».
Описывая старинные способы вычислений и современные приёмы быстрого счёта, мы попытались показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
Современные способы вычислений просты и доступны всем.
При знакомстве с научной литературой обнаружили более быстрые и надежные способы вычислений.
В конце учебного года учащиеся владеют достаточно прочными навыками устных вычислений. Снижается количество ошибок, допускаемых учениками в сложных вычислениях. Действия с рациональными числами выполняются осмысленно, с применением приемов устного счета. Эта методика дает возможность учителям творчески подходить к изучению и повторению тем школьного курса, освобождая время урока для более интересных и нестандартных задач.
Умение учащихся находить процент от числа, изменение величины в процентах, число по его проценту и т.д. позволяет усложнить текстовые задачи, что развивает логическое мышление.
Полезно включить в устные упражнения приемы счета с использованием формул сокращенного умножения.
Эта тема интересует ребят; они находят новые приемы устного счета, что оживляет уроки.
Выводы:
Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.
В школьных учебниках практически нет приемов быстрого счета, поэтому результат данной работы – сборник приемов для быстрого счета будет очень полезным для учащихся.
Литература:
Г. Н. Берман «Приемы быстрого счета» - ОГИЗ, 1947
Я.И. Перельман «Быстрый счет» - Ленинград, 1945
И.Я. Депман, Н.Я . Виленкин «За страницами учебника математики» -М, Просвещение, 1989
Я.И. Перельман «Занимательная арифметика» - М, Транзиткнига, 2005
Приложение I
Анкета
1. Зачем нужно уметь считать?
а) пригодится в жизни, например, считать деньги;
б) чтобы хорошо учиться в школе;
в) чтобы быстро решать;
г) чтобы быть грамотным;
д) не обязательно уметь считать.
2. Перечисли, при изучении каких школьных предметов тебе понадобится правильно считать?
а) математика; б) литература; в) география; г) технология;
д) музыка; е) физическая культура; ж) ОБЖ; з) информатика;
и) русский язык;
3. Знаешь ли ты приемы быстрого счета?
а) да, много; б) да, несколько; в) нет, не знаю.
4. Применяешь ли ты при вычислениях приемы быстрого счета?
а) да; б) нет.
5. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?
а) да; б) нет.
Приложение II
Зачем нужно уметь считать?
П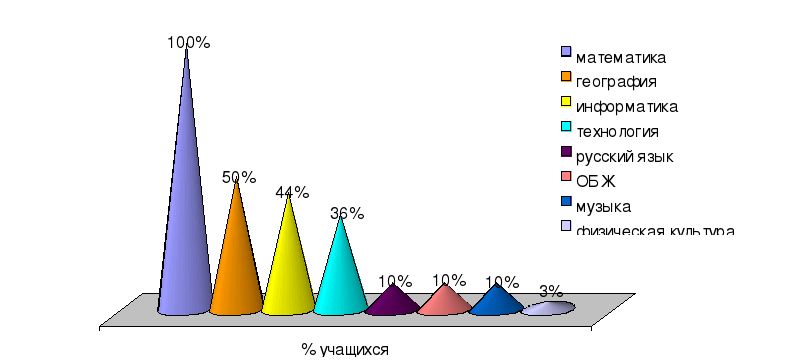 ри изучении каких школьных предметов тебе понадобится правильно считать?
ри изучении каких школьных предметов тебе понадобится правильно считать?
Памятка быстрого счета Приложение III
| Умножение и деление числа на 4. Чтобы умножить число на 4, нужно его дважды умножить на 2. Например: 26·4=(26·2)·2=52·2=104; 417·4=(417·2)·2=834·2=1668. Чтобы разделить число на 4, нужно его дважды разделить на 2.Например: 324:4=(324:2):2=162:2=81. | Умножение и деление числа на 5. Чтобы умножить число на 5, нужно его умножить на 10 и разделить на 2.Например: 236·5=(236·10):2=2360:2=1180. Чтобы разделить число на 5, нужно умножить 2 и разделить на 10, т.е. отделить запятой последнюю цифру. Например: 236:5=(236·2):10=472:10=47,2. | Умножение двузначного числа на 11 При умножении двузначного числа на 11, нужно между цифрой единиц и цифрой десятков вписать сумму этих цифр, причем, если сумма цифр больше 10, то единицу нужно прибавить к старшему разряду (первой цифре). Например:
23·11=253, т.к. 2+3=5, поэтому между 2 и 3 ставим цифру 5;
57·11=627, т.к. 5+7=12, цифру 2 ставим между 5 и 7, а к 5 прибавляем 1, вместо 5 пишем 6. |
| Умножение числа на 9. Чтобы умножить число на 9, нужно к нему приписать 0 и отнять исходное число. Например: 72·9=720-72=648. | Умножение на 25 числа, делящегося на 4. Чтобы умножить на 25 число, делящееся на 4, нужно его разделить на 4 и получившееся число умножить на 100. Например:124·25=(124:4)·100=31·100=3100 | Умножение числа на 1,5. Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину. Например: 34·1,5=34+17=51; 146·1,5=146+73=219. |
| Умножение двузначного числа на 101. Для того, чтобы число умножить на 101, нужно приписать данное число к самому себе. Например:34·101 = 3434. Поясним, 34·101 = 34·100+34·1=3400+34=3434.
| Возведение в квадрат двузначного числа, оканчивающегося на 5. Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25.
Например: 352=1225, т.е. 3·4=12 и к 12 приписываем 25, получаем 1225. | Возведение в квадрат двузначного числа, начинающегося на 5. Для возведения в квадрат двузначного числа, начинающегося на пять, нужно прибавить к 25 вторую цифру числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0. Например:
522= 2704, т.к. 25+2=27 и 22=04;
582= 3364, т.к. 25+8=33 и 82=64. |

 Получите свидетельство
Получите свидетельство Вход
Вход



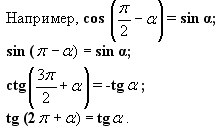

 ри изучении каких школьных предметов тебе понадобится правильно считать?
ри изучении каких школьных предметов тебе понадобится правильно считать?








 Исследование по матемтаике "Приемы быстрого счета" (0.15 MB)
Исследование по матемтаике "Приемы быстрого счета" (0.15 MB)
 1
1 3056
3056 206
206 Нравится
0
Нравится
0


