Логарифмы и их свойства

Определение логарифма.

Логарифмом числа b по основанию a называется показатель степени , в которую нужно возвести основание а , чтобы получить число b .

(где b0, a0 , a≠1 )

Его обычно называют основным логарифмическим тождеством.

= b

Примеры:

log 5 25 = 2, 5 2 = 25 ; Для того, чтобы получить число 25, необходимо умножить 5 на себя в 2 раза.

log 4 = - 2, т.к. =

т.к. = 27.

т.к.

0, a≠1 и любых x0 и y0 выполнены равенства: logₐ 1 = 0 logₐ a = 1 logₐ x·y = logₐ x + logₐ y logₐ = logₐ x - logₐ y logₐ xᵖ = p·logₐ x , для любого действительного p . " width="640"

Основные свойства логарифмов

При любом a0, a≠1 и любых x0 и y0 выполнены равенства:

logₐ 1 = 0

logₐ a = 1

logₐ x·y = logₐ x + logₐ y

logₐ = logₐ x - logₐ y

logₐ xᵖ = p·logₐ x , для любого действительного p .

0; a ≠ 1; b 0; c 0. пример: 3 " width="640"

1. Логарифм произведения положительных чисел равен сумме логарифмов множителей. log a (bc) = log a b + log a c

a 0; a ≠ 1; b 0; c 0.

пример:

3

0; a ≠ 1; b 0; c 0. пример: 1 " width="640"

2. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя.

b

= log a b – log a c,

log a

c

a 0; a ≠ 1; b 0; c 0.

пример:

1

0; a ≠ 1 b 0; r R log a b r = r log a b пример: 1,5 " width="640"

3. Логарифм степени с положительным основанием равен показателю степени, умноженному на логарифм основания

a 0; a ≠ 1

b 0;

r R

log a b r = r log a b

пример:

1,5

Формула перехода от одного основания логарифма к другому

Десятичные логарифмы

Десятичным логарифмом числа называют логарифм этого числа по основанию 10

log 10 a = lg a

lg 10 = 1

lg 100 = lg 10² = 2

ДОПОЛНИТЕЛЬНЫЕ СООТНОШЕНИЯ

• log a a c = c;

Найдите логарифм по основанию a числа, представленного в виде степени с основанием a

№ 476 а) 9

№ 477 а)

№ 478 а)

=

Проверьте справедливость равенств.

№ 479 а) ;

№ 480 в)

Найдите логарифмы данных чисел по основанию

№ 483 а)

25,

;

, ;

;

Найдите число

№ 484 а)

;

№ 486 б)

2, ; def

Запишите число в виде логарифма с основанием

№ 487 а) 2; =4

Упростите выражение:

№ 488 а)

Упростите выражение:

№ 489 г) 9

==

№ 490 а)

==9

Найдите =?

log a x = ; x

Пример

Найдём х, если

log 5 x = log 5 7 + 2log 5 3 - 3log 5 2.

Решение:

log 5 x = log 5 7 + log 5 3 2 - log 5 2 3 =

= log 5

log 5 x = ;

x =

Пример: Найдём значение выражения Решение:

lg 72 – lg 9 = lg = lg 8 = 3lg 2;

lg 28 – lg 7 = lg = lg 4 = 2lg 2;

Следовательно,

==

Ответ:

10

Логарифмы в деятельности человека

в астрономии

электротехнике

животноводстве

в музыке

в экономике

в технике

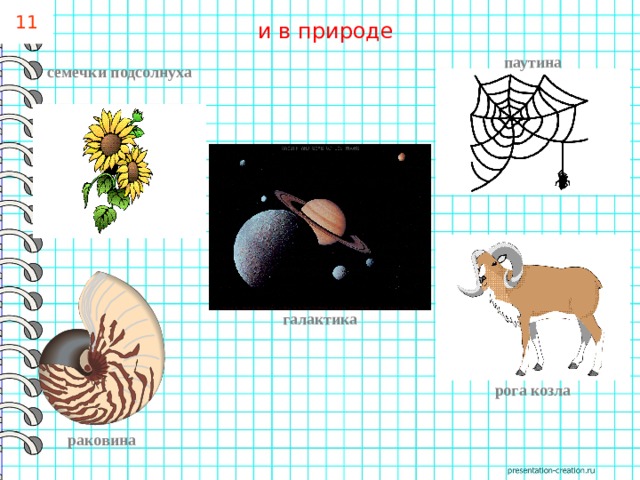
11

и в природе

паутина

семечки подсолнуха

галактика

рога козла

раковина

ДОМА! Найдите значение выражения Вычислить:

log 7 49; log 3 1/81; log 1/2 8; log 4 1;

lg 10000; lg 0,001;

log 6 3 + log 6 2;

log 5 100 – log 5 4;

lg 0,18 – lg 180

2. Подготовить презентацию:

« Из истории логарифмов»,

« Логарифмы в деятельности человека »

всем спасибо за участие!