Специально для учителей!

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Разработки / Математика / Уроки / 10 класс / Логарифмические уравнения

Логарифмические уравнения

Урок "Логарифмические уравнения" 10 класс, является уроком обобщения знаний для учащихся 10 классов. На этом уроке рассматриваются различные способы решения логарифмических уравнений. Осуществляется отработка навыков решения уравнений: уравнения, решаемые по определению логарифма, уравнения, решаемые потенцированием, уравнения, решаемые приведением к одному основанию, уравнения, решаемые логарифмированием.

Истомина Лариса Георгиевна

06.05.2017

Содержимое разработки

Тема урока: "Логарифмические уравнения" Цели урока:

Обобщить и систематизировать знания учащихся по данной теме.
Закрепить основные методы решения логарифмических уравнений, предупредить появление типичных ошибок.
Предоставить каждому из учащихся проверить свой уровень подготовки по данной теме.

Оборудование: доска, мультимедийный проектор, ватман, маркеры.

Раздаточный материал: дифференцированные задания для самостоятельной работы, индивидуальные задания.

Ход урока

I. Организационный момент

Сообщение учителем темы, целей и задач урока, его основных моментов.

II. Проверка теоретических знаний

Фронтальный опрос класса:

Что называется уравнением?
Что называется корнем уравнения?
Что значит “решить уравнение”?
Какие уравнения называются равносильными?
Что понимают под логарифмическим уравнением?
Что в первую очередь находят в логарифмических уравнениях? Одновременно двое учеников записывают формулы на доске.
ОДЗ?
Решить уравнение устно

1. log2 (x – 13) + log2 ( 1 – х ) = 3 2. log5 (x – 2) = 2 log5 (3 – х )

Диктант (с последующей взаимопроверкой) Возможные ответы: “да” — + , “нет” — –

В-1				В-2
Верно ли утверждение:				Верно ли утверждение:
1	Если 2^х = 7, то х = log₂7	+	1		Если 3^х = 8, то х = log₈3	–
2	Если log₃х = 3, то х = 6	–	2		Если log₇49= х, то х =– 2	–
3	Если log_х64= 2, то х = 8	+	3		Если log₂х = 4, то х = 16	+
Равносильны ли уравнения:				Равносильны ли уравнения:
4	lgх² = 6 и 2 lg = 6,	+	4		lgх² = 4 и 2 lg х = 4,		–
5	lgх ^. lg5= 3 и lg(х +5)= 3	–	5		lgх+lg(х²– 1)= 2 и lgх(х²– 1)= 2		+
6	lg= 1 и lgх – lg(х +3)= 1	+	6		и lgх – lg4 = 2		–

III. Повторить основные виды логарифмических уравнений по предлагаемому образцу

1) Уравнения, решаемые по определению логарифма.

2) Уравнения, решаемые потенцирование.

3) Уравнения, решаемые приведением к одному основанию.

4) Уравнения, решаемые логарифмирование.

5) Уравнения, решаемые приведением к квадратному уравнению.

Выбери уравнения, соответствующие каждому виду, и, используя ключ, составь слово: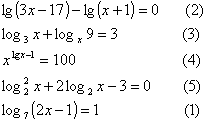

Джон НЕПЕР
(1550-1617) Шотландский математик, изобретатель логарифмов. Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд «Описание удивительных таблиц логарифмов» опубликовал лишь в 1614.

IV. Карточки для групп для защиты способа решения логарифмических уравнений:

карточки для групп	тип	ответ
уравнения	тип	ответ
1) log₂log₃ log₄ (6x+ 4) = 0
2) log₃² x – log₃x = 2
3) log₂ (x+13) = 2 log₂ (x+1)
4)x ^{lgx +5} = 10 ^15+3lgx
5) log₃x + 2 log_x3 = 3

Ответы .Карточки для групп для защиты способа решения логарифмических уравнений:

уравнения	тип	ответ
карточки для групп	тип	ответ
1) log₂log₃ log₄ (6x+ 4) = 0	Уравнения, решаемые по определению логарифма.	x =10.
2) log₃² x – log₃x = 2	Уравнения, решаемые приведением к квадратному уравнению.	x=; 9.
3) log₂ (x+13) = 2 log₂ (x+1)	Уравнения, решаемые потенцирование.	x = 3.
4) x ^{lgx +5} = 10 ^15+3lgx	Уравнения, решаемые логарифмирование.	x = 0,00001; 1000.
5)log₃x + 2 log_x3 = 3	Уравнения, решаемые приведением к одному основанию.	x=3; 9.

Самостоятельная работа с последующей самопроверкой

Каждый из учащихся может сам проверить свой уровень подготовки к ЕГЭ по данной теме. Ученикам предлагается тест, содержащий задания трех уровней сложности и бланк для ответов.

Вариант1

Часть 1
А1	Укажите промежуток, которому принадлежит корень уравнения:
	1) ; 2) [15; 18]; 3) ; 4) (-16,5; 16,5)
А2	Найдите корень уравнения:
	1) 6; 2) -3; 3) -6; 4) 3
А3	Найдите произведение корней уравнения
	1) 13 2) -36 3) 32 4) 9
Часть 2
В1	Найдите целые корни уравнения

Вариант2

Часть 1
А1	Укажите промежуток, которому принадлежит корень уравнения:
	1) ; 2) ; 3) ; 4)
А2	Найдите корень уравнения:
	1) -7; 2) -3; 3) 7; 4) 3
А3	Найдите произведение корней уравнения
	1) 1000; 2) 0.1; 3)100; 4)10
Часть 2
В1	Найдите сумму корней уравнения

Вариант 3

Часть 1
А1	Решите уравнение
	1) 29; 2) 7; 3) 25; 4) 11
А2	Укажите промежуток, которому принадлежит корень уравнения:
	1) ; 2) [0; 1]; 3) ; 4)
А3	Найдите сумму корней уравнения
	1) ; 2) ; 3) 25; 4)
Часть 2
В1	Найдите целые корни уравнения

Вариант4

Часть 1
А1	Решите уравнение :
	1) 6,5; 2) ; 3) ; 4) 5,5
А2	Найдите корень уравнения:
	1)7; 2) -7; 3) 0; 4)
А3	Найдите сумму корней уравнения :
	1) 27; 2) ; 3) ; 4)
Часть 2
В1	Решите уравнение :

Бланк ответов
Ф.И.
Номер варианта
А1	А2	А3	В1

Ответы к тестам:

_{Вариант}^{Задания}	А₁	А₂	А₃	В₁
1	2	1	3	4
2	4	4	1	12
3	3	2	4	49
4	4	1	2	16

V. Итог урока

Мы повторили основные методы решения логарифмических уравнений. Каждый из вас проверил свой уровень подготовки к ЕГЭ по теме “Логарифмические уравнения” и сделает для себя соответствующие выводы.

Дома: 1) Решить уравнение, заполнив пропуски.