Логарифмические уравнения

основанию

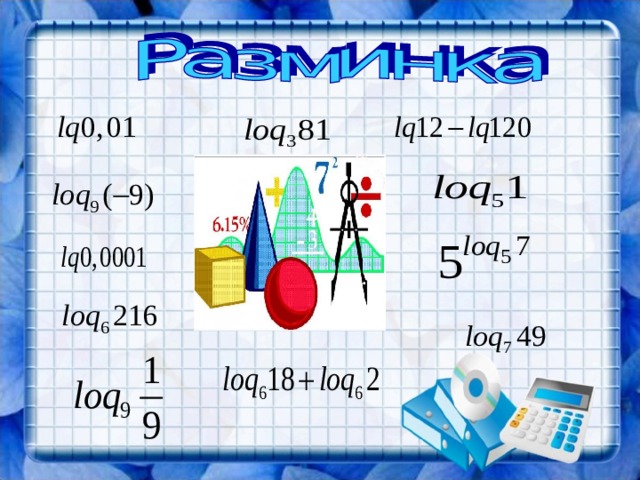
1. Логарифмом числа b по …………… а

называется …………….. степени, в которую

нужно……………. основание а, чтобы

получить число b .

2. Основание и число, стоящее под знаком

логарифма, должны быть………….

3. Если основание а =….., то такой логарифм

называется десятичным и обозначается lg b .

показатель

возвести

положительными

10

a?

Логарифм и ОДЗ

Log a b =Х

а х = b

Логарифм и ОДЗ

ВМЕСТЕ

трудятся

везде!

b?

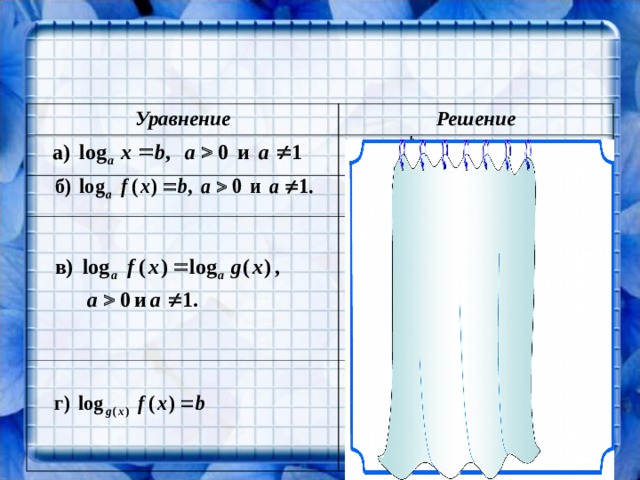
Методы решения

Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, что, следуя нашему методу, мы достигли цели.

Лейбниц

Пути решения уравнений

1

2

3

• Решить уравнение, выбрав метод решения
• Проверить найденные корни непосредственной подстановкой в исходное уравнение (не всегда корректно)

• Найти область допустимых значений (ОДЗ) переменной
• Решить уравнение, выбрав метод решения
• Выяснить, удовлетворяют ли корни решённого уравнения ОДЗ

• Заменить уравнение равносильным уравнением или равносильной системой

Уравнение

Решение

X=24

X=10

X=-10 и X =10

log 2 x+4log 4 x= 12

X=16

x=64

x lgx =100x;

0 2) Т. к. обе части уравнения положительны, то прологарифмируем их по основанию 10, получим lg x lgx = lg( 100x); lgx·lgx=lg ( 100 х) lg 2 x = lg 100 + lg х lg 2 x – lg х- 2=0 х =100, х=0,1 Ответ : х =100, х =0,1 " width="640"

Цель ?

Проблема ?

x lgx =100x;

• ОДЗ : х 0

2) Т. к. обе части уравнения положительны, то прологарифмируем их по основанию 10, получим

lg x lgx = lg( 100x);

lgx·lgx=lg ( 100 х)

lg 2 x = lg 100 + lg х

lg 2 x – lg х- 2=0

х =100, х=0,1

Ответ : х =100, х =0,1

0 2) Т. к. обе части уравнения положительны, то логарифмируя их по основанию 10, получим: lg x lgx+2 = lg 1000 ( lgx+2)·lgx=lg1000 lg 2 x+ 2lgx- 3=0 lgx = y у 2 + 2у- 3=0 y =- 3 , у=1. lgx =- 3 , x =10 -3 =0,001; lgx =1, x =10 Ответ: 0,001; 10. " width="640"

Первичное закрепление

X lgx+2 = 1000

1)ОДЗ : Х 0

2) Т. к. обе части уравнения положительны, то логарифмируя их по основанию 10, получим:

lg x lgx+2 = lg 1000

( lgx+2)·lgx=lg1000

lg 2 x+ 2lgx- 3=0

lgx = y

у 2 + 2у- 3=0

y =- 3 , у=1.

lgx =- 3 , x =10 -3 =0,001;

lgx =1, x =10

Ответ: 0,001; 10.

Решите уравнения методом логарифмирования

x 0,5lgx =0,01x 2 ;

X 2log 3 x =3 log 3 3x

0 2) lg x 0,5lgx = lg 0,01x 2 ; 0,5lgxlgx – (-2+2lgx)=0 0,5lg 2 x - 2lgx+2=0 lg 2 x - 4lgx +4 =0 (lgx -2) 2 =0 l gx =2 х=100 Ответ : х=100 X 2log 3 x =3 log 3 3x 1)ОДЗ : х 0 2) log 3 X 2log 3 x = log 3 3 log 3 3x 2log 3 x·log 3 x=log 3 (3x)·log 3 3 2log 3 2 x = 1+log 3 x 2log 3 2 x -1-log 3 x=0 X=10 или х=3 -0,5 Х= √3/3 Ответ : х=10, Х=√3/3 " width="640"

Самопроверка

x 0,5lgx =0,01x 2 ;

1)ОДЗ : х 0

2) lg x 0,5lgx = lg 0,01x 2 ;

0,5lgxlgx – (-2+2lgx)=0

0,5lg 2 x - 2lgx+2=0

lg 2 x - 4lgx +4 =0

(lgx -2) 2 =0

l gx =2

х=100

Ответ : х=100

X 2log 3 x =3 log 3 3x

1)ОДЗ : х 0

2) log 3 X 2log 3 x = log 3 3 log 3 3x

2log 3 x·log 3 x=log 3 (3x)·log 3 3

2log 3 2 x = 1+log 3 x

2log 3 2 x -1-log 3 x=0

X=10 или х=3 -0,5

Х= √3/3

Ответ : х=10,

Х=√3/3

0 2) Т. к. обе части уравнения положительны, то прологарифмируя их по основанию 5, получим lоg 5 x lоg 5 x = lоg 5 x 10 ; lоg 2 5 х = 10lоg 5 x lоg 2 5 х -10lоg 5 x =0 lоg 5 x(lоg 5 x -10) =0 Lоg 5 x =0 или lоg 5 x = 10 х =1 или х = 5 10 Ответ : х =1 или х = 5 10 " width="640"

x lоg 5 x =x 10 ;

1)ОДЗ : х 0

2) Т. к. обе части уравнения положительны, то прологарифмируя их по основанию 5, получим

lоg 5 x lоg 5 x = lоg 5 x 10 ;

lоg 2 5 х = 10lоg 5 x

lоg 2 5 х -10lоg 5 x =0

lоg 5 x(lоg 5 x -10) =0

Lоg 5 x =0 или lоg 5 x = 10

х =1 или х = 5 10

Ответ : х =1 или х = 5 10

ДЖОН НЕПЕР (1550-1617)

• Шотландский математик –

изобретатель логарифмов.

В 1590-х годах пришел к идее

логарифмических вычислений

и составил первые таблицы

логарифмов, однако свой знаменитый

“ Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.

• Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.

3

1

2

4

5

6

7

л

о

г

8

а

р

и

ф

м

н о ь

о с н в а н и е

ч а с т н о о

п о к з а т е л ь

н е п е

д е с я т ч н ы й

л о г а р и м и р о в а н и е

с у м е