
Презентация к уроку математики по теме «Логарифмы и их свойства. Основное логарифмическое тождество. Натуральные и десятичные логарифмы»
Автор: Савинова Лариса Николаевна – преподаватель ГБОУ СПО
«Орехово-Зуевский промышленно-экономический колледж имени Саввы Морозова»
Московской области

Логарифмы и их свойства. Основное логарифмическое тождество. Натуральные и десятичные логарифмы.
Дидактическая цель
- дать понятие логарифма с произвольным основанием;
- сформировать навыки вычисления логарифмов по определению;
- овладеть знаниями и умениями использовать основное логарифмическое тождество, формулы логарифмирования и потенцирования, формулы перехода от одного основания к другому в процессе решения упражнений;
- дать понятие натурального и десятичного логарифма;
- овладеть умением вычислять логарифмы с помощью микрокалькулятора.

- Основные знания и умения
- Студенты должны
- знать :
- определение логарифма числа; основное логарифмическое тождество; свойства логарифмов; определение натурального и десятичного логарифма; формулу перехода к новому основанию;
- определение логарифма числа;
- основное логарифмическое тождество;
- свойства логарифмов;
- определение натурального и десятичного логарифма;
- формулу перехода к новому основанию;
- логарифмировать выражения по данному основанию;
- вычислять значения простейших логарифмических выражений, используя определение и свойства логарифма;
- решать простейшие логарифмические уравнения;
- вычислять логарифмы на микрокалькуляторе.

1. Определение логарифма
- Рассмотрим показательное уравнение
- При это уравнение не имеет решений; при показательное уравнение имеет единственный корень. Этот корень называют логарифмом b по основанию а и обозначают .

Определение.
- Логарифмом положительного числа b по основанию а , где , называется показатель степени, в которую надо возвести основание а , чтобы получить число b , т.е.

Формулу
(где ) называют основным логарифмическим тождеством.
На определение логарифма возможны три типа упражнений:
- на определение логарифма по данному числу и данному основанию;
- определение основания логарифмирования по числу и логарифму;
- определение числа по логарифму и основанию.

Примеры. Заполнить пропуски :
1.
2.
3.
4.
5.
6.

Примеры. Заполнить пропуски :
7.
8.
9.
10.

Примеры.
11. Вычислить

Примеры.
12. ;
13. Решить уравнение

2. Свойства логарифмов
- При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:
- При любом и любых положительных чисел х и у выполнены равенства:

Свойства логарифмов:
1.
2.
3.
логарифм произведения равен сумме логарифмов:
4. логарифм частного равен разности логарифмов:
5. логарифм степени равен произведению
показателя степени на логарифм основания этой степени:

- Основные свойства логарифмов широко применяются в ходе преобразований выражений, содержащих логарифмы. При этом используются формулы перехода от одного основания логарифма к другому основанию:
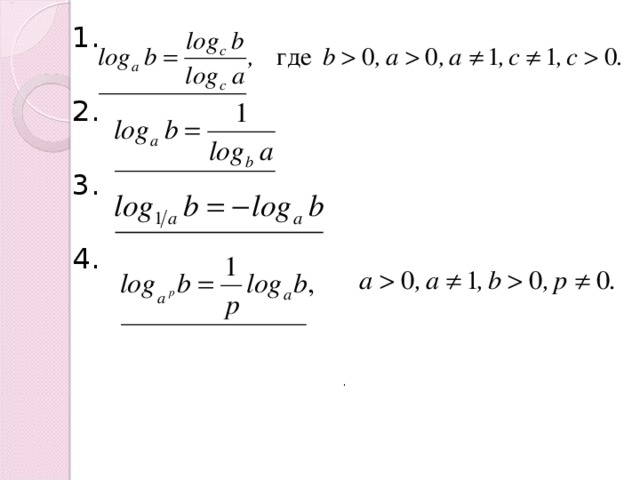
1.
2.
3.
4.
.

Примеры:
14.
15.
16.
17.
18.

Примеры:
14.
15.
16.
17.
18.

3. Логарифмирование и потенцирование
- Действие нахождения логарифма числа называют логарифмированием .
- Если число х представлено алгебраическим выражением, содержащим числа a , b , c , ..., то найти логарифм этого выражения – значит выразить логарифм числа х через логарифмы чисел a , b , c , .... Нахождение положительного числа по его логарифму называют потенцированием .

Примеры.
19. Прологарифмировать выражения:
Ответ.

20. Пропотенцировать выражения:
Ответ.

4. Десятичные и натуральные логарифмы .
- Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут:
- Натуральным логарифмом числа называют логарифм этого числа по основанию е , где
– иррациональное число, и пишут:

- Натуральные и десятичные логарифмы связаны формулами

Вычисление логарифмов на микрокалькуляторе.
- Вычисление числа е на микрокалькуляторе проводится по программе:
1 SHIFT e x Ответ: 2,718281829.
- Вычисление числа lg b и ln b проводится по программе:
b lg и b l п .
- Например , вычисляя lg 13 и ln 13 , набираем на микрокалькуляторе:
13 lg Ответ: 1,113943352;
13 l п Ответ: 2,564949358.

- Чтобы находить логарифмы чисел по любому основанию, достаточно знать значения только десятичных или только натуральных логарифмов. Для этого используется формула перехода от логарифма по одному основанию к логарифму по другому основанию
- Из этой формулы при с = 10 и с = е получаются формулы перехода к десятичным и натуральным логарифмам:

Пример. С помощью микрокалькулятора вычислить
.
.
- Запишем данный логарифм следующим образом:
или
- Вычисляем на микрокалькуляторе по программе:
80 lg / 3 lg = 3,988692535
80 l п / 3 l п = 3,988692535

Закрепление материала Ответьте на вопросы:
- Что называется логарифмом? Записать на доске основное логарифмическое тождество. Чему равен логарифм произведения? Чему равен логарифм частного? Чему равен логарифм степени? Почему Запишите формулы перехода логарифма от одного основания к другому. Что такое десятичный логарифм и как он записывается? Что такое натуральный логарифм и как он записывается?
- Что называется логарифмом?
- Записать на доске основное логарифмическое тождество.
- Чему равен логарифм произведения?
- Чему равен логарифм частного?
- Чему равен логарифм степени?
- Почему
- Запишите формулы перехода логарифма от одного основания к другому.
- Что такое десятичный логарифм и как он записывается?
- Что такое натуральный логарифм и как он записывается?

Вычислите устно:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Упростить выражения, пользуясь основным логарифмическим тождеством:

Найти число х по определению логарифма:

Итоги занятия
- На уроке изучили логарифмы и их свойства.
- Обобщили понятие степени с действительным показателем и закрепили навыки действий со степенями.
- Вывели формулы перехода логарифма от одного основания к другому.
- Студенты развивали умение быстро и правильно вычислять логарифмы «в уме» и с помощью микрокалькулятора.
- Студенты научились логарифмировать и потенцировать выражения.
- Закрепили умения вычислять логарифмические выражения, используя определение, свойства логарифма и формулы перехода.

Итоги занятия
- Внимание студентов было обращено на приемы оформления, рациональную запись решения, на умение пользоваться математической символикой в процессе решения упражнений.
- На занятии воспитывались аккуратность, внимательность при решении упражнений, способности доводить любое учебное задание до конца, правильно оценивать результаты своей работы, усиливалось внимание к развитию творческого мышления и повышению интереса к предмету «математика».

Домашнее задание
- Учебник: Алгебра и начала анализа: учебник для 10-11 кл.: стр. 233 – 235 прочитать; материал изучить по конспекту.
- Выполнить упражнения: № 477, 481, 484, 490, 491 (б, г), 493, 495.


 Получите свидетельство
Получите свидетельство Вход
Вход
















































 Логарифмы и их свойства (0.82 MB)
Логарифмы и их свойства (0.82 MB)
 0
0 3026
3026 104
104 Нравится
0
Нравится
0











