
Современное образование в ДНР
7 класс Алгебра «Линейная функция»
Подготовила учитель математики «МОУ Школа №106 г.Донецка»
Лепетухина Е.Н.

Тип урока : урок усвоения новых знаний
Форма урока : комбинированный
Цели урока : сформировать определение линейной функции и представление о ее графике; формировать умение выделять линейную функцию из множества функций; формировать умение строить график линейной функции;
Развитие умения анализировать и делать выводы; развитие исследовательской и познавательной активности учащихся при выявлении роли параметров k и b в расположении графика линейной функции;
Воспитание аккуратности, интереса к предмету через использование компьютера на уроке.
Оборудование : компьютерная презентация, индивидуальные компьютеры с графическим редактором; карандаши, линейки.

Ход урока :
Оргмомент: (компьютеры включены) - 3 мин.
Приступаем к изучению нового материала.
В тетради для конспектов запишите тему и дату урока.

Линейная функция – это функция, которую можно задать формулой
y=kx+m, где x – независимая переменная, k и m – некоторые числа.
Применяя эту формулу, зная конкретное значение x, можно вычислить соответствующее значение y.
Пусть y=0,5x−2.
Тогда:
если x=0, то y=−2 ;
если x=2, то y=−1;
если x=4, то y=0 и т.д.
Обычно эти результаты оформляют в виде таблицы:
x 0 2 4
y −2 −1 0
x - независимая переменная (или аргумент),
y - зависимая переменная

Графиком линейной функции y=kx+m является прямая .
Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.
Построим на координатной плоскости xOy точки (0;−2) и (4;0) и
проведём через них прямую.
![Пример: Построить график линейной функции: y=−2x+1,x∈[−3;2] Составим таблицу значений функции: x −3 2 y 7 −3 Построим на координатной плоскости xOy точки (−3;7) и (2;−3) и проведём через них прямую. Далее выделим отрезок, соединяющий построенные точки. Этот отрезок и есть график линейной функции y=−2x+1,x∈[−3;2]. Точки (−3;7) и (2;−3) на рисунке отмечены тёмными кружочками.](https://fsd.videouroki.net/html/2018/09/01/v_5b8a780268b6e/img5.jpg)
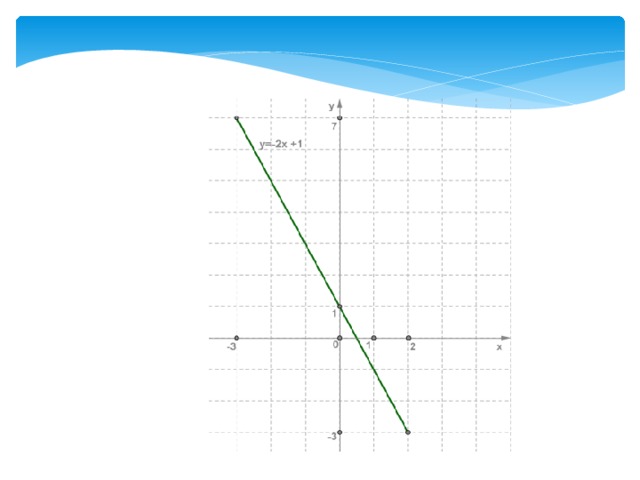
Пример:
Построить график линейной функции:
- y=−2x+1,x∈[−3;2]
Составим таблицу значений функции:
x −3 2
y 7 −3
Построим на координатной плоскости xOy точки (−3;7) и (2;−3) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции y=−2x+1,x∈[−3;2].
Точки (−3;7) и (2;−3) на рисунке отмечены тёмными кружочками.
 0, то линейная функция y=kx+m возрастает; если k" width="640"
0, то линейная функция y=kx+m возрастает; если k" width="640"
Рассматривая график линейной функции на отрезке, можно назвать наибольшее и наименьшее значение линейной функции.
y=−2x+1,x∈[−3;2] имеем, что y наиб=7 и y наим =−3 .
В ходе построения графиков линейных функций, можно как бы «подниматься в горку» или «спускаться с горки», т.е. линейная функция или возрастает или убывает.
Если k0, то линейная функция y=kx+m возрастает;
если k

Построение графика линейной функции сводится к нахождению
координат двух точек, так как её график — прямая.
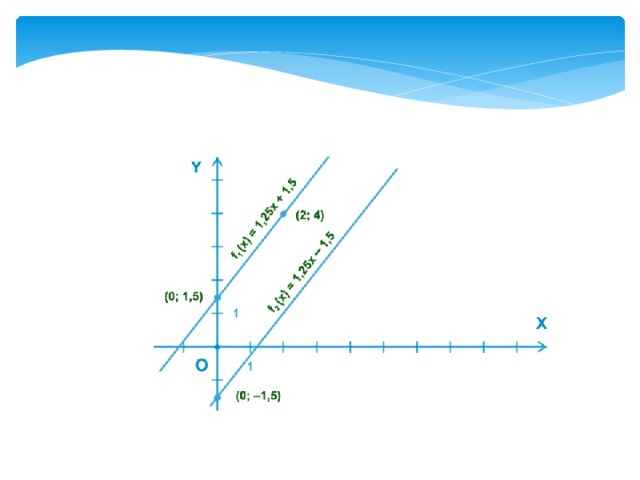
Построим графики двух функций:
f1(x) = 1,25x + 1,5 и f2(x) = 1,25x – 1,5 .
Первая точка f1(0) = 1,5 :
x = 0 ; y = 1,5 т. к. y = 1,25x + 1,5 ⇒ y = 1,25 • 0 + 1,5 = 1,5 .
Вторая точка f1(2) = 4 :
x = 2 ; y = 4 т. к. y = 1,25x + 1,5 ⇒ y = 1,25 • 2 + 1,5 = 4 .

Задания для закрепления материала
1 Назовите функции , графики которых : а) параллельны ; б)пересекаются? в) пересекаются в одной точке?
1) y=-2x-1 ; y=-2x-3,5 ; y=-2x+5
2) y= - 0,5x ; y=0,5x-3 ; y=1,5x+5
3) y= - 0,3x-4 ; y=0,3x-4 ; y=3x-4

2.Задайте формулой линейную функцию , график которой параллелен прямой y=- 8x - 11 и проходит через начало координат.

3.При каком значении x значение функции y=-0,5x + 1 равно 5
а)x=8 б)x=-8 в)x=-9

4.Какие точки принадлежат графику линейной функции
y= -0,5x+1 :
а) A(-1;0) б) B(-2;2,5) в) .C(-2;0) г) .D(0;1)

5.Найдите координаты точек пересечения графика линейной функции у= 2х+2 с осями координат

6. Найдите координаты точки пересечения графиков линейных функций
у= х-6 и у=-0,5х

7.В магазине купили учебник за 150 рублей и 15 тетрадей по n рублей.
Сколько денег уплатили за покупку?
Составьте выражение к задаче, обозначив стоимость С, найдите его при n = 5,8,16.

Решение.
1) Найдём стоимость тетрадей С 1= 15n;
2) Тогда стоимость всей покупки С= С1+150 или С= 15n+150, найдём значение C:
при n = 5, С = 15•5 + 150, С= 225;
при n = 8, С = 15•8 + 150, С= 270;
при n = 16, С = 15•16+ 150, С= 390.

Подведение итогов
Объявление оценок с аргументацией
Запись домашнего задания
Урок окончен. Спасибо за урок.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Линейная функция (284.73 KB)
Линейная функция (284.73 KB)
 0
0 647
647 35
35 Нравится
0
Нравится
0


