Лекция "Решение неравенств с одной переменной"

Решением неравенства называют всякое значение переменной 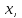которая обращает заданное неравенство с переменной в верное числовое неравенство. Иногда используют термин частное решение. Множествo всех частных решений неравенства называют общим решением, но чаще всего употребляют термин решение. Таким образом, термин решение используют в трех смыслах: как общее решение, как частное решение и как процесс, но обычно по смыслу бывает ясно о чём идёт речь.

Определение 1. Два неравенства с одной переменно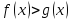й и 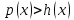называют равносильными, если их решения (то есть множества частных решений) совпадают.

Использование в определении знака «» непринципиально, можно и в этом определении и во всех утверждениях, имеющихся в данном параграфе использовать любой другой знак неравенства, как строгого, так и нестрогого.

Определение 2. Если решение неравенства 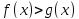является решением неравенства 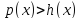, то неравенство 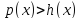называется следствием неравенства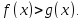

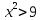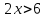Пример 1. а) Найдем решения неравенств (1) и (2):

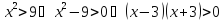
Решаем это неравенство с помощью метода интервалов:

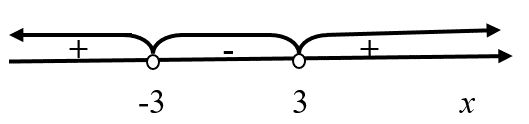
Рисунок 1

Получаем: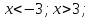

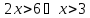
Нанесем оба решения на одну координатную прямую: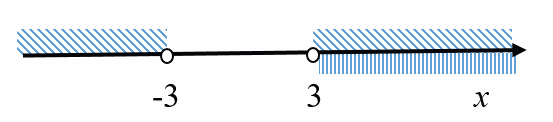

Рисунок 2

сверху – решение неравенства (1);

снизу – решение неравенства (2).

Мы видим, что решение неравенства (2) составляет лишь часть решения неравенства (1).

Это означает, что неравенство (2) – следствие неравенства (1)

б) Рассмотрим те же неравенства (1) и (2), но заменим в них знак «» на «

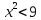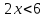(3) и (4):

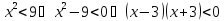
Найдем решение этого неравенства с помощью метода интервалов, обратимся к рисунку 1: 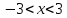– решение неравенства (3).

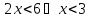– решение неравенства (4).

Нанесем найденные решения на одну координатную прямую:

сверху – решение неравенства (3);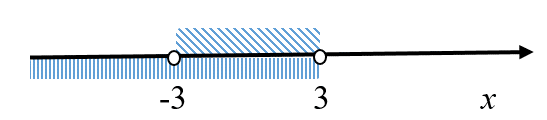

Рисунок 3

снизу – решение неравенства (4).

Из рисунка мы видим, что неравенство (3) является следствием неравенства (4), так как

решение неравенства (4) включает в себя решение неравенства (3).

Теорема 1. Если какой-либо член неравенства перенести из одной части неравенства в другую с противоположным знаком, оставив знак неравенства без изменения, то получится неравенство, равносильное данному.

Пример 2. Решить неравенство: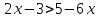

Решение. Решаем по принципу «известные в одну сторону, неизвестные – в другую»

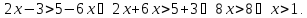
Теорема 2. Если обе части неравенства возвести в одну и ту же нечетную степень, оставив знак неравенства без изменения, то получится неравенство, равносильное данному.

Пример 3. Решить неравенство: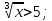

Решение.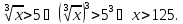

Теорема 3. Показательное неравенство 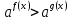равносильно:

а) неравенству того же смысла , если ;

б) неравенству противоположного смысла ,

если .

Пример 4. Решить неравенство: ; б)

Решение.

б)

Теорема 4. а) Если обе части неравенства , умножить на одно и тоже выражение , положительное при всех из области определения (области допустимых значений переменной) неравенства , оставив при этом знак неравенства без изменения, то получится неравенство , равносильное данному.

б) Если обе части неравенства , умножить на одно и тоже выражение , отрицательное при всех из области определения (области допустимых значений переменной) неравенства , изменив при этом знак неравенства на противоположный, то получится неравенство , равносильное данному.

Пример 5. Решить неравенство:

Решение. так как в знаменателях дробей стоит одно и то же выражение и при этом т и тем более Тогда по теореме 4 часть а) мы имеем право умножить обе части неравенства на одно и то же выражение и при этом знак неравенства останется прежним:

разделим обе части неравенства на (-3) и при этом (по теореме 4 часть б)) поменяем знак неравенства на противоположный: .

Теорема 5. Если обе части неравенства неотрицательны в области его определения (в ОДЗ), то после возведения обеих частей неравенства в одну и туже четную степень получится неравенство того же смысла, равносильное данному.

Теорема 6. Если , то логарифмическое неравенство равносильно:

а) неравенству того же смысла , если

б) неравенству противоположного смысла , если

Примеры для теорем 5 и 6 будут рассмотремы более конкретно далее.

Определение 3. Говорят, что несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все такие значения переменной, каждое из которых является частным решением всех заданных неравенств.

Значение переменной, при котором каждая из неравенств системы обращается в верное числовое неравенство, называют частным решением системы неравенств. Множество всех частных решений системы неравенств представляет собой общее решение системы неравенств чаще говорят просто решение системы неравенств.

Решить систему неравенств значит найти все ее частные решения.

Решение системы неравенств представляет собой пересечение решений неравенств, образующих систему.

Определение 4. Говорят, что несколько неравенств с одной переменной образует совокупность неравенств, если ставится задача найти все такие значения переменной, каждое из которых является решением хотя бы одного из заданных неравенств.

Каждое такое значение переменной называют частным решением совокупности неравенств. Множество всех частных решение совокупности неравенств представляет собой решение совокупности неравенств.

Решение совокупности неравенств представляет собой объединение решений неравенств, образующих совокупность.

Неравенства, образующие систему, объединяются фигурной скобкой, а неравенства, образующие совокупность, квадратной скобкой. Для неравенств, образующих совокупность, допустима запись в строчку через точку с запятой.

При решении систем неравенств и совокупностей неравенств неравенство – следствие можно отбросить.

Пример 6. Решить систему и совокупность неравенств:

а) б)

Решение.

а)

Решением системы неравенств будет пересечение решений неравенств системы, то есть промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем луч .

Рисунок 4

Решением совокупности неравенств будет объединение решений неравенств совокупности. В рассматриваемом примере получаем открытый луч - промежуток, на котором имеется хотя бы одна штриховка.

Ответ: а) ; б)

Если в системе из нескольких неравенств одно является следствием другого (или других), то неравенство-следствие можно отбросить. Рассмотрим пример решения логарифмического неравенства.

Пример 7. Решить неравенство

Решение. Рассмотрим данное неравенство. Левая часть неравенства – логарифм. Правая часть – число. Для того, чтобы можно было использовать теорему 6, необходимо представить число - 4 в виде логарифма по основанию :

Тогда получаем:

Так как - основание логарифма и , то используем теорему 6 часть б):

«избавляемся» от знака логарифма и знак неравенства меняем на противоположный:

При решении логарифмических неравенств обязательным является нахождение ОДЗ (выражение под знаком логарифма обязательно должно быть большим нуля), т.е.

.

Из этих двух неравенств получаем систему неравенств:

Если выполняется второе неравенство системы, то автоматически выполняется и первое (если , то тем более ). Значит, первое неравенство - следствие второго и его можно отбросить. Решая второе неравенство, находим:

Решение данного неравенства находим с помощью метода интервалов:

Рисунок 5

Значит:

Ответ. .

В теореме 6 говорилось о том, что если , то логарифмическое неравенство равносильно:

а) неравенству того же смысла , если

б) неравенству противоположного смысла , если

Значит, если , то при решении неравенства мы можем перейти к равносильной системе неравенств:

первые два неравенства – это ОДЗ переменной для исходного неравенства.

Обратим внимание на то обстоятельство, что в составленной системе есть одно лишнее неравенство:

Рисунок 6

по свойству транзитивности неравенств можно сделать вывод, что . Это значит, что первое неравенство системы является следствием второго и третьего неравенства. А неравенство-следствие можно отбросить. Таким образом, данную систему можно заменить более простой системой неравенств

Аналогично, при от неравенства мы можем перейти к равносильной системе неравенств:

Рисунок 7

первые два неравенства – это ОДЗ переменной для исходного неравенства. Точно так же можно установить (по свойству транзитивности неравенств), что неравенство в полученной системе будет неравенством-следствием неравенств и его можно отбросить, а систему, определяющую решение исходного логарифмического неравенства можно заменить на более простую систему:

Пример 8. Решить неравенство

Решение. Рассмотрим два случая:

1. 2)

Рассмотрим случай 1)

1-е. Записываем ОДЗ:

по теореме 6, часть а) «освобождаемся» от знаков логарифмов, знак неравенства сохраняется: .

Из всех этих условий получаем систему неравенств:

Рассмотрим случай 2)

Аналогично:

ОДЗ:

по теореме 6 часть б) «избавляемся» от знаков лограрифмов, знак неравенства меняется на противоположный:

Значит, имеем еще одну систему неравенств:

Таким образом, что заданное логарифмическое неравенство равносильно совокупности двух систем неравенств:

Решаем первую систему неравенств:

Используем метод интервалов:

Рисунок 8

Таким образом, из рисунка 8 получаем:

Решаем вторую систему:

Используем метод интервалов:

Рисунок 9

Таким образом,

Решением исходного логарифмического неравенства являестся совокупность решений двух систем:

Ответ.

Обсудим решение неравенства вида (1)

Во-первых, запишем условие, определяющее ОДЗ:

Во-вторых, заметим, что при данное неравенство не имеет решений, значит, можно сразу потребовать выполнения условия

.

В-третьих, заметим, что при указанных условиях обе части неравенства неотрицательны, значит, если по теореме 5 возвести их в квадрат, получим неравенство, равносильное данному.

Таким образом, иррациональное неравенство (1) равносильно системе неравенств

Обсудим решение неравенства вида . (2)

Во-первых, запишем условие, определяющее ОДЗ: .

Во-вторых, заметим, что при справедливость неравенства не вызывает сомнений (поскольку ). Это значит, что решения системы неравенств являются одновременно и решениями неравенства (2).

В-третьих, заметим, что если , то обе части неравенства не отрицательны (мы, естественно, учитываем, что ). Значит, если по теореме 5 возвести их в квадрат, получим неравенство, равносильное данному.

Таким образом, иррациональное неравенство равносильно совокупности систем неравенств:

первое неравенство второй системы можно опустить (подумайте, почему).

Пример 9. Решить неравенства:

а) ; б)

Решение. а) Данное неравенство равносильно системе неравенств:

Рисунок 10

для решения квадратного неравенства необходимо найти корни квадратного трехчлена , а для этого нужно решить квадратное уравнение

Таким образом, . Геометрическая иллюстрация помогает найти решение неравенства:

Второе неравенство уже решено:

Из третьего неравенства находим:

.

С помощью геометрической иллюстрации находим решение системы неравенств:

Таким образом,

Рисунок 11

б) Данное неравенство равносильно совокупности систем неравенств:

и

Рассмотрим первую систему: в предыдущем задании мы уже находили ОДЗ : Если при этом еще , то получаем:

Рисунок 12

Во второй системе можно опустить первое неравенство, поскольку оно является следствием третьего неравенства системы. Это позволяет переписать вторую систему в более простом виде: .

Рисунок 13

Эта система не имеет решений. Значит, решение совокупности систем неравенств совпадает с решением первой системы: .

Ответ: а) б)

Неравенства, содержащие переменную под знаком модуля, решаются различными способами. Мы покажем эти способы на достаточно простом примере.

Пример 5. Решить неравенство .

Решение.

Первый способ. Имеем:

Геометрически выражение означает расстояние на координатной прямой между точками . Значит, нам нужно найти все такие точки , которые удалены от точки 2,5 более чем на 2, - это точки из промежутков

Рисунок 14

Итак, мы получили следующие решения неравенства:

Второй способ. Поскольку обе части заданного неравенства неотрицательны, то по теореме 5 возведение их в квадрат есть равносильное преобразование неравенства. Получим:

Воспользовавшись тем, что , получим:

Рисунок 15

Применив метод интервалов,

получим: .

Третий способ. Выражение может быть не отрицательным или отрицательным. Если , то, и заданное неравенство принимает вид .

Если , то, и заданное неравенство принимает вид .

Таким образом, получаем совокупность двух систем неравенств:

Решая первую систему, получаем:

Решая вторую систему, получаем:

Объединяя найденные решения двух систем неравенств, получаем:

Ответ:

Из указанных трех способов наиболее универсальным является третий. Но поскольку он представляется достаточно сложным с технической точки зрения, то, если возможно, стараются использовать второй и первый способы.

Пример 6. Решить неравенство .

Решение. Здесь можно применить два из указанных в предыдущем примере способов решения: 1) рассмотрение двух случаев знака выражения, содержащегося под знаком модуля, и сведение заданного неравенства к совокупности и систем неравенств; 2) возведение обеих частей неравенства в квадрат.

Первый способ. Если , то , и заданное неравенство принимает вид .

Если , то , и заданное неравенство принимает вид . Таким образом, задача сводится к решению совокупности двух систем неравенств:

1. Решим первое неравенство первой системы. Найдем корни уравнения

   Рисунок 16

; получим: .

С помощью метода интервалов находим решение неравенства:

2) Решим второе неравенство первой системы, но сначала преобразуем его к более простому виду: . Найдем корни уравнения

Рисунок 17

С помощью метода интервалов

находим решение неравенства:

Рисунок 18

3) Oтметив найденные решения первого и второго неравенств на координатной прямой, находим пересечение решений: Это решение первой системы неравенств.

4) Решим первое неравенство второй системы. С помощью геометрической иллюстрации, представленной на рисунке 16, получаем решение неравенства:

5) Решим второе неравенство второй системы, но сначала преобразуем его к более простому виду:

6) Отметив найденные решения первого и второго неравенств на координатной прямой, находим пересечение решений:.

Рисунок 19

Это решение второй системы неравенств.

7) Объединив найденные решения систем неравенств

Второй способ. Перепишем данное неравенство в виде

Отсюда следует, что . Значит, обе части заданного неравенства неотрицательны, и мы имеем право возвести их в квадрат. Получим систему неравенств:

Решим первое неравенство этой системы:

Рисунок 20

Откуда находим:

Решим второе неравенство системы:

Корни квадратного трехчлена найдены выше: . С их помощью составим разложение трехчлена на множители:

Это позволяет переписать последнее неравенство так:

Отметим точки на координатной прямой и расставим знаки функции

Рисунок 21

на полученных промежутках. Это геометрическая иллюстрация позволяет сделать вывод о решении неравенства

Итак, для первого неравенства системы получили для второго неравенства системы получили: . Значит, решение системы таково:

.

Ответ:

5