Максимова И.В. МБОУ «СОШ № 4», г. Черногорск
Методическая разработка
урока алгебре в 8 классе
Тема урока: Квадратные уравнения. Решение квадратных уравнений
Тип урока: урок обобщения и систематизации знаний с применением компьютерных технологий.
Методы обучения: Проблемный, наглядный, коммуникативный, частично-поисковый. Данные методы обеспечивают высокую результативность в работе и, главное, развитие мышления учащихся, их познавательных интересов.
Формы обучения: Фронтальная, групповая, индивидуальная
Приемы деятельности учителя: Проблемное изложение нового материала; организация поисковой работы в группах; самостоятельной работы обучающихся; оценка работы обучающихся и коррекция.
Оборудование и материалы к уроку
Оборудование, ТСО: 1. Компьютер, интерактивная доска.
2. Дидактический материал к уроку: Презентация к уроку, тест, задания № 4 модуль «Алгебра» (ОГЭ 2017).
Планируемый результат обучения, в том числе и формирование УУД:
Познавательные УУД: поиск и выделение необходимой информации для решения квадратных уравнений; выбор методов решения квадратных уравнений в зависимости от их типа; выдвижение.
Коммуникативные УУД: сотрудничество в поиске и сборе информации; умение выражать свои мысли.
Регулятивные УУД: прогнозирование, контроль, коррекция, рефлексия, оценка, саморегуляция.
Личностные УУД: формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний.
Ход урока.
Организационное начало урока
Герберт Спенсер, английский философ, когда-то сказал: “Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы”.
Проверим, кто из вас порадовал бы Герберта Спенсера.
2. Сообщение темы и цели урока.
А) постановка проблемы.
- Посмотрите на доску. Это лишь некоторые задания экзаменационной работы 9 класса. На сегодняшний день мы не знаем многих тем и алгоритмов решения некоторых заданий.
Но как вы думаете, что их объединяет?
Для их выполнения нужно уметь решать квадратные уравнения.
Применение тестовой системы приводит к необходимости в быстром решении уравнений. Поэтому мы должны научиться приемам, которые помогут экономить время и эффективно решать квадратные уравнения.
- А что для этого нужно знать? (способы решения квадратных уравнений)
Тема урока «Квадратные уравнения. Способы их решения»
- Как вы думаете, как можно сформулировать цель нашего урока исходя из его темы?
- Другими словами обобщить и систематизировать весь предшествующий опыт решения квадратных уравнений. А зачем нам это надо?
(Для возможности выбора рационального пути решения).
- Итак, наша цель: обобщить опыт решения квадратных уравнений, научиться выбирать рациональный путь решения.
- Откройте тетради. Запишите число. Классная работа.
3. Обобщение и систематизация знаний.
а) актуализация знаний учащихся.
- Вспомним, как традиционно решаются квадратные уравнения.
- Какое уравнение называется квадратным?
- От чего зависит количество корней квадратного уравнения?
- По какой формуле вычисляется дискриминант ?
Закончите таблицу (3 ученика к доске)
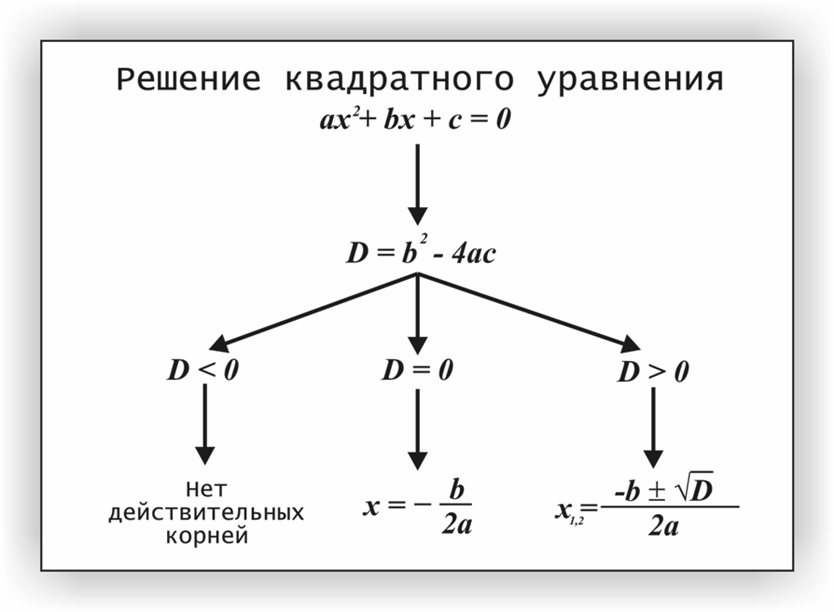
- Понятие Д придумал английский ученый Сильвестр, он называл себя даже “математическим Адамом” за множество придуманных терминов.
- Проверим составленную таблицу.
- Количество корней квадратного уравнения зависит от дискриминанта.
Проведем цифровой диктант.
- Вычислим дискриминант.
- Укажите количество корней уравнения 2, 1 или 0.
|
| Дискриминант | Число корней |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Запишите полученное пятизначное число.
|
| Дискриминант | Число корней |
|
| 0 | 1 |
|
| -8 | 0 |
|
| 45 | 2 |
|
| 12 | 2 |
|
| -25 | 0 |
Проверка 10220
- Можно ли, не решая уравнения, определить, имеет ли оно корни или нет?
(Да, можно. Уравнение всегда имеет корни, если первый коэффициент и свободный член имеют противоположные знаки.)
- А если они одного знака?
-(Тогда надо находить дискриминант)
Имеет ли корни квадратное уравнение 2x2+5x−7=0?
1) применение формул корней квадратного уравнения.
Задание 1. Решите уравнение 2x2+5x−7=0. (самостоятельно)
- К какому виду относится следующее квадратное уравнение x2−7x=8.
(приведенное)
- Какую теорему используют для решении приведенных квадратных уравнений ?
(т. Виета)
- Напомним формулировку теоремы Виета и обратной ей.
- Знаменитый французский учёный Франсуа Виет(1540-1603) был по профессии адвокатом. Свободное время он посвящал астрономии. Занятия астрономией требовали знания тригонометрии и алгебры. Виет занялся этими науками и вскоре пришёл к выводу о необходимости их усовершенствования, над чем и проработал ряд лет.
Виет сделал много открытий, но сам он больше всего ценил зависимость между корнями и коэффициентами квадратного уравнения, которая теперь называется «теоремой Виета».
«Если числа m и n таковы, что их сумма равна – р, а произведение равно q, то эти числа являются корнями уравнения х2 + p x + q = 0».
- Как будем рассуждать при подборе корней этого уравнения x2−7x- 8=0.
2) подбор корней с применением теоремы Виета
Задание 2. Найдите корни квадратного уравнения x2 −7x - 8=0. (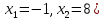
Задание 3. Пусть х1 и х2 – корни квадратного уравнения х2+7х-11=0.
- Не решая уравнения, найдите значение выражения 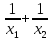 .
.
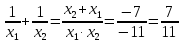
- Какую теорему применили?
Задание 4. Работа в группах.
Решить уравнения, составить таблицу.
Таблица 1. (Группа 1,3)
|
| a | b | c | a+b+c |
|
|
|
| 2 | 5 | -7 | 0 | 1 |
|
|
| 4 | -9 | 5 | 0 | 1 |
|
|
| 9 | -4 | -5 | 0 | 1 |
|
| | 7 | -1 | -6 | 0 | 1 | |
Вывод: Если в квадратном уравнении ах2 + вх + с = 0 сумма коэффициентов равна нулю (а + в + с = 0), то один из корней равен 1, а другой .
|
| a | b | c | a-b+c |
|
|
| | 1 | -7 | -8 | 0 | -1 | 8 |
| | 3 | -2 | -5 | 0 | -1 | |
| | 2 | -1 | -3 | 0 | -1 | |
| | 10 | 3 | -7 | 0 | -1 | |
Вывод: Пусть дано квадратное уравнение ах2 + вх +с = 0. Если а – в + с = 0 или в = а + с, то х1 = –1, х2 = – .
Запись на доске и в тетрадях.
| Уравнение | Свойство коэффициентов | Корни уравнения |
|
| а + b+ с = 0 | х1 = 1, |
| а – b + с = 0 или b = а + с |
х1 = - 1, |
|
|
|
|
|
|
|
|
Это ещё один способ решения квадратных уравнений
3) применение свойств коэффициентов.
Задание 5. Выберите уравнения, которые можно решить, используя это свойство?
Запишите корни.
203х2+220х+17=0
5x2−9x+4=0.
x2+6x−16=0
25х2 – 20х – 5 = 0
2х2 – 11х + 15 = 0.
Проверка
- Чем удобен это способ?
( позволяет устно найти корни уравнения)
Помимо традиционных методов решения квадратных уравнений есть еще специальные и общие методы. Рассмотрим каждый из специальных методов в отдельности. И оценим его “перспективы”.
4) Метод “переброски” старшего коэффициента.
В некоторых случаях удобно решать сначала не данное уравнение ax2 + bx + c = 0, а приведенное y2+by+ac=0, которое получается из данного “переброской” коэффициента а, а затем разделить найденные корни на а для нахождения корней исходного уравнения. и
Пример: решите уравнение
2х2 - 9х - 5=0
заменим приведенным квадратным уравнением с “переброской” коэффициента а
( D0 ), по теореме, обратной теореме Виета, подбором найдем корни
вернемся к корням исходного уравнения
Ответ: 5; -0,5
Замечание: метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.
Задание 6. Решение одного уравнения разными способами.
Решите уравнение х2 - 4х + 3 = 0 различными методами
- У доски 5 обучающихся. Метод, которым придется решать, написан в произвольно выбираемой карточке: 1) по общей формуле; 2) по формуле с четным вторым коэффициентом; 3) по теореме Виета; 4) по сумме коэффициентов; 5) графическим способом.
- Каким из способов проще и быстрее решить данное уравнение?
Задание 7. Тестирование с самопроверкой.
-Чтобы проверить, как вы умеете применять, полученные знания выполним тест. (Приложение 1.)
Время выполнения теста 5 - 7 минут. Выпишите буквенный код в тетрадь.
| Номер задания | Вариант ответа | |
| Вариант - 1 | Вариант - 2 | |
| 1 | В | Г |
| 2 | Г | Б |
| 3 | Г | А |
| 4 | В | В |
| 5 | А | А |
- Свои предварительные результаты вы можете узнать уже сейчас. Проверьте правильность выполнения заданий. Критерии выставлении оценки следующие :
Критерии оценки
«5» - 5 заданий
«4» - 4 задания
«3» - 3 задания
«2» - 1 – 2 задания
4. Подведение итогов.
– Какие способы решения квадратных уравнений существуют.
- Это, конечно, далеко не все способы решения квадратных уравнений.
- Итогом нашей работы будет: заполнение этой блок схемы (фреймана) начнем в классе, а дома вы ее должны продолжить. А так же к каждому виду и способу решения придумать свое уравнение, и решить его. Оформить фреймон необходимо на альбомном листе.
Приложение1 Презентация «Квадратные уравнения»
Тест по теме «Квадратные уравнения»
Вариант 1 ЧАСТЬ 1
А1. Найдите сумму корней уравнения: .
1) -0,25 2) корней нет 3) 0,25 4) 12
А2. Найдите произведение корней уравнения: .
1) -0,5 2) 1 3) 0,5 4) 5
А3. Найдите произведение корней уравнения: .
1) -14 2) 7 3) -7 4) 4
А4. Сколько действительных корней имеет уравнение .
1) 1 2) 2 3) 3 4) ни одного
А5. Сколько действительных корней имеет уравнение . 1) 4 2) 2 3) 3 4) ни одного
А6. Сколько действительных корней имеет уравнение .
1) 3 2) 2 3) 1 4) ни одного.
А7. Найдите значение коэффициента а, если в уравнении один из корней уравнения равен -1.
1) -14 2) -12 3) -2 4) -1
А8. Найдите значение коэффициента b, если в уравнении один из корней уравнения равен 2.
1) -4 2) 4 3) -2 4) 2
А9. Запишите квадратное уравнение, имеющее корни .
1) 2)
3)
4)
А10. Найдите сумму корней уравнения: .
1) 2) корней нет 3)
4)
ЧАСТЬ 2
В1. Найдите корни уравнения:
Вариант 2 ЧАСТЬ 1
А1. Найдите сумму корней уравнения: .
1) -5 2) 5 3) 2,5 4) -2,5
А2. Найдите произведение корней уравнения: .
1) -0,75 2) 1,5 3) 0,5 4) 0,75
А3. Найдите произведение корней уравнения: .
1) 70 2) -4 3) -70 4) -35
А4. Сколько действительных корней имеет уравнение .
1) 1 2) 2 3) 3 4) ни одного
А5. Сколько действительных корней имеет уравнение . 1) 1 2) 2 3) 3 4) ни одного
А6. Сколько действительных корней имеет уравнение .
1) 3 2) 2 3) 1 4) ни одного.
А7. Найдите значение коэффициента а, если в уравнении один из корней уравнения равен -1.
1) 3 2) -13 3) -3 4) -1
А8. Найдите значение коэффициента b, если в уравнении один из корней уравнения равен 2.
1) -4 2) -7 3) -2 4) -14
А9. Запишите квадратное уравнение, имеющее корни .
1) 2)
3)
4)
А10. Найдите сумму корней уравнения: .
1) 10 2) 6 3) корней нет 4) 4
ЧАСТЬ 2
В1. Найдите корни уравнения: .
Ответы:
| Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | В1 |
| 1 | 3 | 3 | 3 | 1 | 1 | 3 | 2 | 1 | 3 | 4 | 0 |
| 2 | 4 | 2 | 4 | 4 | 1 | 3 | 2 | 2 | 4 | 3 | 0 |
Приложение 2
с
НЕПОЛНЫЕ
ПРИВЕДЕННЫЕЕ
ВИДЫ УРАВНЕНИЙ И СПОСОБЫ РЕШЕНИЯ
ПОЛНЫЕ
Дискриминантт

 Получите свидетельство
Получите свидетельство Вход
Вход



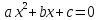
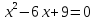
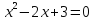
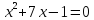
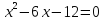
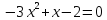
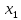
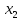
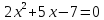
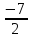
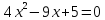
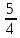
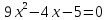









 Квадратные уравнения. Решение квадратных уравнений (805.89 KB)
Квадратные уравнения. Решение квадратных уравнений (805.89 KB)
 0
0 440
440 19
19 Нравится
0
Нравится
0


