| 1 часть |
| Тема. | Какие навыки должны быть приобретены? | Какие модули, формы, действия планируются для развития умений и навыков? |
| 1-2 уроки. Квадратное уравнение. Виды квадратного уравнения. | Вопросы для развития навыков: Знание, понимание: Является ли уравнение квадратным, почему? назовите коэффициенты. Определите приведенные квадратные уравнения, почему уравнение является приведенным. Определите неполные квадратные уравнения. Почему данные уравнения является неполным квадратным? Объясните метод решения каждого вида неполного квадратного уравнения в общем виде, определите количество решений.
Применение Решите неполное квадратное уравнение с объяснениями. Приведите уравнение к квадратному виду. Как вы понимаете это задание, какие действия вы должны сделать? Анализ и синтез: Изучите уравнение вид: 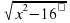 =3 =3 Как решить данное уравнение, какие преобразования надо выполнить?
| Групповая работа. Диалогический метод. Метод исследовательской беседы. Приемы критического мышления. Формативное оценивание по критериям, отметки выставляются в журнал только с согласия ученика. Рефлексия. ИКТ- интерактивная доска. На первом уроке – изучение новой информации и первичное закрепление. Предложить выбрать из данных уравнений квадратные, попросить обосновать выбор. Прочитать определение из учебника, проанализировать свой выбор. Продумать понимание термина «неполные квадратные уравнения». Попросить озвучить и обосновать свое понимание. Прочитать из учебника определение, сопоставить со своим пониманием, откорректировать. Для решения неполного квадратного уравнения рассмотреть решения конкретных уравнений, затем обобщить через коэффициенты. Обратить внимание на наличие и количество корней. Провести рефлексию: закончить предложение «Я узнал…Я научился…, Мне трудно…, Хочу еще раз изучить…» На втором уроке – урок закрепления и развития ЗУН. Организовать деятельность учащихся по постановке собственной цели урока. Деление на группы по видам квадратных уравнений Актуализация и мобилизация: 10 минутная самостоятельная работа по материалам прошлого урока с взаимопроверкой и взаимооцениванием в паре. Решение неполных квадратных уравнений по заданиям учебника в группах. Решение неполных квадратных уравнений по Ершовой в группах. Рассмотреть задания на приведение к квадратному виду. Предложить составить алгоритм действий в решении подобных заданий. Рассмотреть применение знаний в измененных ситуациях, типа 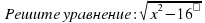 =3 =3 Для подготовки к следующему уроку рассмотреть задания на квадрат двучлена и построение графиков элементарных функций. Самооценивание: Проставить баллы от 0-3 Я знаю, что такое квадратное уравнение. Я определяю его коэффициенты. Я знаю, что такое неполное квадратное уравнение Я решаю неполное квадратное уравнение Я умею приводить уравнение к квадратному виду. Рефлексия: (сравнение с рефлексией прошлого урока) Сегодня мне удалось. Сегодня у меня не получилось… |
| 3-4 уроки. Решение полного квадратного уравнения методом выделения квадрата двучлена и графическим способом. | Вопросы для развития навыков: Знание и понимание: Запишите формулы квадрата двучлена. Запишите трехчлен в виде квадрата двучлена. Можно ли заданный трехчлен записать в виде квадрата двучлена? Почему? Применение Выделите квадрат двучлена в уравнении, решите полученное уравнение. Знание, понимание: Определите пару «формула функции – график». Виды и графики элементарных функций. В чем заключается графический способ решения уравнения? Составьте алгоритм решения уравнения графическим методом. Применение Решение квадратного уравнения графическим методом. Анализ и оценка: В чем недостаток и преимущество изученных способов. Какие виды квадратных уравнений удобно решать подобными методами.
| Групповая работа. Обучение тому как учиться Диалогический метод. Метод исследовательской беседы. Приемы критического мышления. Формативное оценивание по критериям. Лидерство. ИКТ – интерактивная доска. Рефлексия. На первом уроке- совершенствование ЗУН -повторить опорные знания по теме квадратные уравнения, формулы квадрата двучлена, графики элементарных функций, этот материал необходим для выполнения новых заданий. В группах обсуждение вопросов и презентация ответов. Самостоятельный поиск применения формулы квадрата двучлена для решения полных квадратных уравнений. Использование графического метода для решения квадратных уравнений (в группах с последующей презентацией) Рефлексия: Что я узнал сегодня на уроке.. Была ли для меня информация новой… Над чем мне надо поработать…
Второй урок – урок закрепления и совершенствования ЗУН Организовать деятельность учащихся по постановке цели урока. Подобрать задания для групповой работы по вопросам рефлексии учащихся. Организовать групповую работу по закреплению навыков решения квадратных уравнений графическим способом и методом выделения квадрата двучлена. Изучить способ группировки для решения некоторых квадратных уравнений. Оценить методы решения в группах. Провести проверочную работу с целью проверки уровня усвоения материала двух уроков. Самооценивание: Оценить по критериям умение решать полные квадратные уравнения изученными методами. Домашнее задание: одно уравнение решить тремя способами.
|
| 5-6 уроки Формула корней квадратного уравнения. | Вопросы для развития навыков Знание и понимание Какие способы решения полных квадратных уравнений вы знаете? В чем недостаток каждого из способов решения? Что такое дискриминант? Как зависит наличие корней от знака дискриминанта и почему? Какова формула корней квадратного уравнения? Применение Как решить квадратное уравнение? (поэтапный алгоритм) Анализ и оценка: Каковы преимущества и недостатки этого метода решения? | Фронтальная, индивидуальная работа, работа в парах, групповая работа Приемы критического мышления, методы исследовательской беседы, взаимооценивание в парах, работа с одаренными (дифференцированные задания). Работа с учетом ЗБР. ИКТ На первом уроке- изучение новой информации и первичного закрепления. Организовать устную работу по повторению опорных знаний (актуализация знаний). Провести подготовительную работу к выведению формулы корней. Решение задания 1) на выделение квадрата двучлена, где второй коэффициент дробное число, например 7/3 2) привести квадратное уравнение к приведенному виду. Проверка домашнего задания- решение одного уравнения тремя способами. Попросить оценить каждый способ (+ и -) – фронтально. Подытожить, что каждый способ имеет ряд недостатков. Есть ли универсальный способ решения квадратных уравнений? Обратить внимание учащихся на первое задание по выделению квадрата двучлена, где коэффициент дробное число. (ИКТ) Рассмотреть по готовому шаблону выделение квадрата двучлена для трехчлена общего вида с активным участием учащихся (исследовательская беседа) Вывести формулу корней. Сделать акцент на знаках дискриминанта. Организовать работу в парах по закреплению первичных навыков решения квадратных уравнений по формулам. Для продвинутых учеников-задания более сложные, роль консультантов по рядам. Рефлексия.
Второй урок: Урок-практикум – закрепление, совершенствование и развитие ЗУН. Повторение опорных знаний (ИКТ) Закрепление навыков решения квадратных уравнений Решение уравнений в группах, взаимопроверка между группами. Дифференцированные задания. Самостоятельная работа(индивидуально)-формативное (промежуточное) оценивание по критериям Самооценивание по критериям – баллы от 0-3 Я знаю основную формулу корней полного квадратного уравнения Я знаю, как от знака дискриминанта зависит наличие корней квадратного уравнения. Я знаю алгоритм решения квадратного уравнения по формуле корней. Я умею решать квадратное уравнение. Рефлексия Мое настроение после урока
|
| 7-8 уроки Формулы корней квадратного уравнения | Вопросы для развития навыков. Знание, понимание и применение. Запишите формулу корней. Запишите зависимость наличия и количества корней от знака дискриминанта? Есть ли ошибки в следующих решениях и какие? Почему допущены эти ошибки? Объясните, как выполнить задания «Найдите значения переменной, при которых равны выражения» «Не решая уравнения, укажите какие из уравнений имеют действительные корни? Какие уравнения имеют равные действительные корни?» Как найти приближенные значения корней? Анализ, синтез и оценка Исследуйте при каких значениях параметра квадратные уравнения имеют один корень, не имеет корней, имеет два различных корня.
| Групповая работа. Обучение тому как учиться. Приемы критического мышления. Формативное оценивание по критериям. Лидерство. ИКТ – интерактивная доска. Рефлексия. Первый урок-Коррекция, закрепление, совершенствование и развитие ЗУН по теме. Деление по группам по видам квадратных уравнений. (по наличию корней) Повторение опорных знаний – устные упражнения (ИКТ) Задания по группам: решение квадратных уравнений с анализом: Сколько решений, какие решения, какие преобразования необходимо выполнить, обосновать решения, Объяснить выбор действий в зависимости от условия, Объяснить в каких ситуациях получаются иррациональные корни, как найти приближенные значения корней. Второй урок – Совершенствование и развитие ЗУН. В группах решить исследовательскую задачу: Найти значение параметра, при которых уравнения имеет два корня, не имеет корней, имеет один корень с презентацией. Составить квадратные уравнения с различными знаками дискриминанта (обмен уравнениями между группами) Выполнение продвинутых заданий на исследование корней квадратного уравнения. Взаимооценивание групповой работы по критериям. Заполнить таблицу оценивания. Второй урок – совершенствование и развитие ЗУН Рефлексия Я узнал… Я научился… Я должен поработать… Мне непонятно… |
| 9-10 уроки Формулы корней квадратного уравнения | Вопросы для развития навыков. Знание, понимание, применение Запишите формулу корней. Запишите зависимость наличия и количества корней от знака дискриминанта? Есть ли ошибки в следующих решениях и какие? Почему допущены эти ошибки? Как решить уравнение с четным вторым коэффициентом? Как найти Д1 в случае четного второго коэффициента? Какие формулы частного случая вы узнали? Как решить уравнения вида А(х)/а +В(х)/в =С(х)/с, где а, в,с –некоторые числа? Анализ, оценка. В чем преимущество формулы для четного второго коэффициента? Когда можно применить формулы рационального вычисления корней в зависимости от коэффициентов? | Групповая работа. Обучение тому как учиться. Самостоятельный поиск рациональных методов решения. Приемы критического мышления. Исследовательская работа. Формативное оценивание по критериям. Лидерство. ИКТ – интерактивная доска. Рефлексия. Деление на группы методом случайного отбора. Первый урок-развитие навыков решения квадратных уравнений. На уроке рассмотреть рациональные пути решения квадратных уравнений. Квадратные уравнения с четным вторым коэффициентом. Квадратные уравнения, где сумма коэффициентов равна 0. Создать условия для закрепления информации: предложить несколько уравнений для группировки по рациональным способам решений, составить самим аналогичные уравнения и обмен между группами. Закрепление посредством решения уравнений и рефлексия по оцениванию собственной деятельности на уроке. Второй урок- Развитие навыков решения заданий в измененных ситуациях. Практикум по решению квадратных уравнений с различными коэффициентами. Исследовательская работа в группах - рассмотреть решения уравнений в измененных ситуациях, задания уровня С: уравнения с буквенными коэффициентами (параметрами) х2-2ах-3а2=0 уравнения на применение свойств арифметического квадратного корня вида  – 6=0 – 6=0 Вопросы: как применить знания квадратных уравнений для выполнения заданий? почему выбраны эти действия? почему ваш ответ является верным? Самостоятельная работа (дифференцированные задания) с целью проверки ЗУН – проверка и оценивание учителя
Рефлексия Я узнал… Я научился… Я должен поработать… Мне непонятно… Домашнее задание: найти и ознакомиться с информацией об ученом –математике Франсуа Виете.
|
| 11 – 12 уроки Теорема Виета. | Вопросы для развития навыков Знание, понимание, применение. Кто такой Франсуа Виет? Почему он интересует нас при изучении темы квадратные уравнения? Сформулируйте теорему Виета. Примените при решении уравнений. Анализ и оценка Как доказать теорему Виета? Для каких уравнений удобнее применять теорему Виета? Определите по внешнему виду уравнения рациональный способ решения и обоснуйте выбор. Как определить знаки корней, не решая уравнения?
| Групповая работа. Критическое мышление. Оценивание для обучения. ИКТ. Работа с одаренными. Исследовательская деятельность Первый урок – изучение новой информации и первичное закрепление. Деление на группы методом случайного отбора. Организовать целеполагающую деятельность. Бенефис одной задачи: Решить уравнение графическим, выделением полного квадрата, группировкой, формулой квадратного уравнения-Записать плюсы и минусы своего способа решения. Кумулятивная беседа: Какие уравнения называются приведенными? Найдите приведенные квадратные уравнения? Кто такой Франсуа Виет? Почему он нас сегодня интересует? Что вы выяснили? Задание в группах: Решите уравнения и сравните с коэффициентами. Найдите закономерность. Заполнить таблицу, сделать вывод. Сформулировать теорему. Задание в группах: Как доказать теорему Виета? Выслушать мнения. Изучить доказательство самостоятельно по учебнику. Показать доказательство на интерактивной доске. Сформулируйте теорему, обратную теорему Виета Решите задания на применение теоремы Виета –первичное закрепление. Рефлексия. Самооценивание.
Второй урок-закрепление, совершенствование и развитие ЗУН Группы работают в том же составе Организация целеполагающей деятельности с учетом прошлой рефлексии и самооценивания. Проверка домашнего задания в группах. Взаимооценивание. Выполнение в группах заданий на применение теоремы Виета: 1. Устное вычисление корней по теореме Виета. 2. Решение уравнений с помощью формулы корней. 3. Составление квадратных уравнений по заданным корням 4.. Определите знаки корней, не решая квадратное уравнение. Проверочная работа с самооцениванием по критериям Рефлексия. |
| 13-14 уроки | Вопросы для развития навыков Знание, понимание, применение. Какие способы решения квадратных уравнений вы знаете? В каких случаях применяются отдельные способы? Сформулируйте теорему Виета. Запишите формулу корней? Анализ, синтез, оценка Определите лишнее уравнение в группах, обоснуйте выбор. Исследовать: При каких значениях параметра данные уравнения имеют различные корни? Определите корни уравнения, если сумма коэффициентов равна 0.
| Обучение тому как учиться. ИКТ. Лидерство. Работа с одаренными. Групповая работа. Уроки обобщения и систематизации. Деление на однородные по степени усвоения группы (по результатам самостоятельной работы). Целеполагающая деятельность. Дифференцированные задания с учетом необходимости коррекции ЗУН. Повторение опорных знаний. Каждая группа отвечает на вопросы внутри группы, фиксируют правильные и неправильные ответы в таблицах оценивания. Задают по два вопроса другой группе. Задания по группам: разбить на группы заданные квадратные уравнения по определенным признакам. Обосновать свой выбор. Задание по группам: раскрыть свою тему - неполные квадратные уравнения, полные квадратные уравнения с четным вторым коэффициентом, полные квадратные уравнения общего вида, приведенные квадратные уравнения, задания на исследования корней. Задания по группам – практикум по решению квадратных уравнений – индивидуальная работа с обсуждением решений внутри группы и между группами Самооценивание и рефлексия.
|
| 15. Контрольная работа. | Контроль и оценка усвоения ЗУН по теме.
| Работа на 4 варианта, 5 заданий. 1-3 обязательный уровень 4- средний уровень 5 –высокий уровень 6 – задание повышенной сложности (необязательное) Оценивание по критериям.
|
| 2 часть - |
| 16 -17 уроки Рациональные уравнения. Решение дробно-рациональных уравнений. | Вопросы для развития навыков Знание и понимание. Определите целые выражения, дробно-рациональные выражения. Какие изданных уравнений являются линейными, квадратными, дробно-рациональными? Когда дробно-рациональное выражение принимает значение, равное нулю? Что значит выражение не имеет смысла? Когда дробно-рациональное выражение не имеет смысла? Как определить значения переменной, при которых дробно-рациональное выражение не имеет смысла? Применение: Определите корни дробно-рационального уравнения. Анализ и синтез: Составьте алгоритм решения дробно-рационального уравнения. Определите рациональный способ для решения каждого из уравнений. | Диалогическое обучение. Критическое мышление. ИКТ, Оценивание для обучения. Критериальное оценивание. Тип урока-урок изучения новой информации и закрепление полученной информации, развитие навыков. Форма – парная, фронтальная, индивидуальная работа. Подвести к теме урока изучением различных видов уравнений На интерактивной доске записать несколько уравнений. Какие из предложенных уравнений вы можете решить? Назовите уравнения, в знаменателе которых буквенные выражения. Определить тему. Попросить поставить цель для себя.- целеполагающая деятельность. Обобщить, сформулировать общую цель. Актуализировать знания, организовав повторение пропорции, решения линейных уравнений. Что такое уравнение? Как называется уравнение №1? Способ решения линейных уравнений. Как называется уравнение №3 Способы решения квадратных уравнений. Что такое пропорция? Основное свойство пропорции. Какие свойства используются при решении уравнений? Когда дробь равна нулю? Изучение нового: Выбрать уравнения для решения из данных, применяя свойство пропорции, Выбрать уравнения для решения, умножением обеих частей на числовой знаменатель, затем на знаменатель, содержащее переменную. Рассмотреть количество корней уравнения, решая двумя способами, исследовать полученные корни. Ввести понятие постореннего корня. Уточнить на основе практического исследования алгоритм решения дробных рациональных уравнений Первичное осмысление нового материала. Работа в парах. Учащиеся выбирают способ решения уравнения самостоятельно в зависимости от вида уравнения. Задания по учебнику. Учитель контролирует работу, оказывает помощь слабоуспевающим. Самопроверка по готовым ответам Обратная связь-тестирование А) Какие из уравнений являются дробными рациональными? Б) Дробь равна нулю, когда числитель ______________________ , а знаменатель _______________________ . В) Является ли число -3 корнем уравнения №6? Г) Решить уравнение №7. Критерии оценивания задания: «5» ставится, если ученик выполнил правильно не менее 90% задания. «4» - 75%-89% «3» - 50%-74% «2» ставится учащемуся, выполнившему менее 50% задания. Оценка 2 в журнал не ставится, 3 - по желанию Рефлексия |
|
18-19 уроки Решение дробно-рациональных уравнений. |
Вопросы для развития навыков Знание, понимание, применение. Какие уравнения называются дробно-рациональными? Какие корни называются посторонними? Каков алгоритм решения дробно-рациональных уравнений? Определите рациональный путь решения предложенных уравнений. Анализ, синтез, оценка. Обоснуйте ваш выбор способа решения. Исследуйте заданное решение уравнения, дайте оценку способа решения, аргументируйте. Составьте по тексту дробно-рациональное уравнение. |
Обучение в сотрудничестве: групповая работа. ИКТ, лидерство в обучении, обучение талантливых и одаренных, оценивание для обучения. Тип урока: урок закрепления, вторичного осмысления и развития знаний, умений и навыков по теме. Деление на группы-метод случайного отбора, определите вид уравнения: линейные, квадратные, дробно-рациональные, иррациональные. Уравнения записаны на стикерах. Предложить выбор координатора группы, объяснить свое решение (обратить внимание на критерии, которыми был аргументирован выбор лидера). Обсудить выполнение домашнего задания в группах, оценить выполнение. Провести устное повторение фронтально Как сложить или вычесть две дроби с одинаковыми знаменателями? - Как сложить или вычесть две дроби с разными знаменателями - Запишите формулы для нахождения корней квадратного уравнения. Объясните, когда уравнение не имеет корней, имеет один корень, имеет два корня. - Какие виды неполных квадратных уравнений вы знаете? Как они решаются? - Какие уравнения называются дробными рациональными уравнениями? - Как решаются дробные рациональные уравнения? - Оцените заданные решения. Разделить по группам задания на решения дробно-рационального уравнения, требующих разных подходов: использование свойства пропорции, предварительного преобразования уравнения, разложения на множители знаменателей различными способами, составление уравнения по тексту. Решения разбираются на доске и должны быть выполнены всеми учениками в тетрадях. Затем поменять в группах задания, требующих другого подхода к решению, проверку осуществляет другая группа, чей метод был разобран на доске. На втором уроке продумать игровую форму урока с учебной целью определения и формативного оценивания уровня достижения. К примеру. марафон уровневых задач. Игровая форма урока уместна так как это последний урок четверти. Дифференцированные задания позволят создать условия для самостоятельной работы слабоуспевающим и развитию одаренных детей. Обеспечить свободный выбор формы работы: индивидуальная, парная, групповая-создать условия для комфортной работы ученика. Определить критерии оценивания выполненной работы, с последующей рефлексией. Продумать вопросы самооценивания и рефлексии с целью определения самостоятельного направления в развитии навыков в каникулярное время.
|
|
20-урок Тема: Дробно-рациональные уравнения | Вопросы для развития навыков. Знание, понимание, применение. Определите целые выражения, дробно-рациональные выражения. Какие из данных уравнений являются линейными, квадратными, дробно-рациональными? Когда дробно-рациональное выражение принимает значение, равное нулю? Что значит выражение не имеет смысла? Когда дробно-рациональное выражение не имеет смысла? Как определить значения переменной, при которых дробно-рациональное выражение не имеет смысла? Какие корни называются посторонними? Каков алгоритм решения дробно-рациональных уравнений? Анализ. Решение квадратных и дробно-рациональных уравнений, содержащих параметры.
| Обучение в сотрудничестве: групповая работа. ИКТ, лидерство в обучении, обучение талантливых и одаренных, оценивание для обучения, критическое мышление. Тип урока – комбинированный, цель данного типа-повторение, обобщение, систематизация ЗУН по теме, так как этот урок-первый после январских каникул. Форма работы-групповая. Деление на группы – группы смешанного состава, дифференцированный подход, волевым методом, соответственно ошибкам, допущенным в марафоне уровневых задач. Целесообразно подобное деление, так как в каждой группе желательно присутствие продвинутых учеников. Списки подготовить заранее и разложить по столам. Можно организовать игру «найди свое место», создать эмоциональный позитивный настрой. Актуализацию знаний провести через устные упражнения, красочно оформленные на слайдах, можно в форме тестов или математического диктанта. В группах организовать работу по обсуждению решения тех видов заданий, которые вызвали затруднения в марафоне уровневых задач. Предложить выполнение подобных уравнений самостоятельно под контролем консультанта. Рассмотреть в группах решения уравнений с параметрами. Предложить подготовить вопросы для исследования задания и определения направления решения. Обсуждение решений провести на доске, обеспечить четкие критерии взаимооценивания работ. К концу урока –обратная связь – самостоятельная индивидуальная работа - оценивание учителя. Дом. задание на повторение квадратных уравнений и способов решения.
|
| 21 – 22 урок Уравнения, приводимые к квадратным. | Вопросы для развития навыков Знание, понимание, применение. Какое уравнение называется квадратным? Какое уравнение называется приведенным? Какова общая формула решения квадратных уравнений? Какие еще формулы решения вам известны? В каких случаях целесообразно применить каждое из способов решения? Какие уравнения называются биквадратными? Анализ, оценка. Составьте алгоритм решения уравнения способом замены переменной. В каких ситуациях применим данный метод? Какие ошибки возможны при решении уравнения данным методом?
| Групповая работа. Обучение тому как учиться. Диалогическое обучение. Приемы критического мышления. Формативное оценивание по критериям. Лидерство. ИКТ – интерактивная доска. Рефлексия. Тип урока-изучение новой информации. Деление на группы – метод случайного отбора. Актуализация ЗУН: Тест «Продолжить фразу» (с последующим фронтальным обсуждением) Квадратным уравнением называется уравнение вида … Корни квадратного уравнения находятся по формуле … Количество корней квадратного уравнения зависит от … Приведённым квадратным уравнением называется уравнение вида … Способы решения квадратных уравнений: …
Групповые задания: Выделить из предложенных те уравнения, решения которых вы не можете выполнить. Обсудить вид уравнений. Предложить поиск решения, обратиться к другим источникам информации – интернет, учебник. Организовать обсуждение предложенных способов. Провести обобщение, дать определение биквадратного уравнения Продумайте алгоритм. Обсудить фронтально и выполнить запись в тетрадях. Выполнить соответственно алгоритму уравнения в группах (разные). Презентовать решения на доске, ознакомить класс с видом уравнения и способом решения. Взаимооценивание. Дать задания на следующий урок- поиск краткой и интересной информации из истории математики на общую тему - уравнения. К концу двух уроков провести проверочную промежуточную работу по определению уровней усвоения знаний и достижения навыков и умений.
|
| 23-24 урок Уравнения, приводимые к квадратным. | Вопросы для развития навыков Знание, понимание, применение Какие уравнения называются биквадратными? Каков способ решения биквадратных уравнений? Сколько корней может иметь биквадратное уравнение? Какие еще уравнения можно решить методом замены переменных? Анализ, оценка. Кто из математиков внес вклад в решение уравнений третьей и четвертой степеней? Определите количество корней биквадратного уравнения. Обоснуйте ответ. Составьте биквадратное уравнение по корням. | Групповая работа. Обучение тому как учиться. Диалогическое обучение. Приемы критического мышления. Обучение талантливых и одаренных. Формативное оценивание по критериям. Лидерство. ИКТ – интерактивная доска. Рефлексия. Тип урока- совершенствование ЗУН. Деление на группы – метод случайного отбора. Мобилизующее начало-Ознакомление с информацией из истории математики по решению уравнений третьей и четвертой степени. (презентация). Обмен интересными фактами. Проверка домашнего задания через обсуждение в группах, в случае необходимости обратиться к консультантам из других групп. Обратная связь – проверка и оценка первичных ЗУН -индивидуальное решение уравнений- самопроверка через готовые ответы. Самооценивание. В группах поиск решений уравнений в измененных ситуациях повышенного уровня сложности – учебник, уровень С. Сборник Галицкого. Презентация решений с обсуждением между группами. Вопросы: Можно ли явно «видеть» выражение для замены? Какие предварительные преобразования надо выполнить? Какая замена оптимальна? Почему? Какой этап решения является наиболее важным для вас? Почему? Исследуйте ответ. К концу уроков самостоятельная работа из дифференцированных заданий. Проверка и оценивание учителя. Обеспечить критериальное оценивание. Рефлексия. |
| 25 урок Тема Решение текстовых задач на составление квадратных уравнений. | Вопросы для развития навыков. Знание, понимание, применение. Найдите линейное уравнение, соответствующее тексту задачи. Какие объекты присутствуют в задаче? Какая взаимосвязь между этими объектами? Величину какого объекта целесообразнее обозначить переменной х? Почему? Как выразить остальные величины задачи через х? Почему? Какое условие позволит составить уравнение? Какое уравнение получилось? Решите уравнение. Анализ и оценка. Все ли данные задачи использованы? Являются ли решения уравнения решением задачи? Почему?
| Диалогическое обучение. Критическое мышление. Оценивание для обучения. ИКТ. Обучение одаренных и талантливых. Тип урока- изучение новой информации. Информация является новой только в части составления квадратного уравнения. Ученики умеют решать задачи на составление линейных уравнений и их систем, поэтому при изучении темы данного урока надо максимально опираться на имеющиеся знания и практический опыт. Форма урока-фронтальная, индивидуальная, парная. Актуализацию знаний провести через устные упражнения по составлению линейного уравнения по тексту задачи и обратной задачи-написанию текста по готовому уравнению, здесь создаются условия для решения задачи развития математически грамотной речи как устной, так и письменной. Важно: необходимость четкого осознания различных соотношений между описываемыми в тексте задачи объектами.
На первом уроке повторить этапы процесса решения задачи: Этапы решения текстовых задач: 1. Анализ содержания задачи. 2. Поиск пути решения задачи и составление плана ее решения. 3. Осуществление плана решения задачи. 4. Проверка решения задачи. Организовать фронтальное обсуждение этапов решения и составить общую схему решения текстовых задач на составление уравнений: 1.Выбор и обозначение неизвестных. 2.Составление уравнений с использованием неизвестных и всех условий задачи. 3.Решение полученных уравнений 4.Отбор решений по смыслу задачи. Рассмотреть решения задач на числа и применение теоремы Пифагора. Учебник: № 202, 204, 210,211. Обратная связь. Самостоятельное решение задачи на составление квадратного уравнения – дифференцированное по выбору ученика. Самооценивание по критериям, критерии должны включать знание всех этапов решения текстовой задачи. Рефлексия: Какой этап решения уравнения составляет трудность для тебя и почему? |
| 26-29 уроки Решение текстовых задач на движение, работу, смеси и сплавы. | Вопросы для развития навыков Знание, понимание, применение. Каковы этапы решения текстовой задачи? Какова схема решения задачи? Какова функция каждого этапа решения задачи? Какие виды движения рассматриваются в задачах? Какова ключевая формула движения? Как найти проценты от числа? Как найти число по его проценту? Какова связь между объемом работы и затраченным временем? Какова формула совместной работы? Решите задачу. Анализ и оценка. Исследуйте условие задачи, классифицируйте задачу. Исследуйте ответ задачи. Соответствует ли уравнение условию задачи? Почему? Оцените выбранную схему записи плана решения.
| Групповая работа. Обучение тому как учиться. Диалогическое обучение. Приемы критического мышления. Обучение талантливых и одаренных. Формативное оценивание по критериям. Лидерство. ИКТ – интерактивная доска. Рефлексия. Типы уроков-закрепление и совершенствование умений и навыков по решению текстовой задачи разного содержания. Деление на группы- группы смешанного состава, по уровню усвоения материала, составлено учителем. Обосновано традиционной сложностью темы для школьников и необходимостью наличия консультантов и направляющей единицы в группе. На трех уроках оставить группу в одном составе, на четвертом уроке составить новые группы методом случайного отбора для обеспечения взаимодействия с другими учащимися и обмена информацией. Мобилизующее начало-анализ результатов самостоятельной работы, корректировка допущенных ошибок обсуждением в группе, затем фронтально. Фронтально: Повторение этапов решения задачи. Обсуждение домашних задач в группе. Далее, на первом уроке - решение текстовых задач на движение, следующий урок -решение задач на работу, следующий урок -решение задач на смеси и сплавы, на четвертом уроке – комбинированный урок по решению задач различного содержания. Определить четкие критерии достижения уровня решения задач каждого вида, создать условия для самоконтроля и самооценивания результатов. Создание в группах кластеров по решению текстовых задач. Составить в процессе обсуждения советы по решению текстовых задач. К примеру, задачи на движение: 1. Записываем формулу-ключ: S = Vt. 2. Определяемся с иксом, расписываем через икс все данные. Особое внимание на величины, входящие в формулу-ключ: путь, скорость, время. Эти величины – основа решения задач на движение. Показать оформление информации в виде таблицы. 3. До составления уравнения, привести (если надо) все величины задачи к единым единицам измерения. 4.Составить уравнение. 5. Решаем уравнение. 6. Исследовать корни уравнения. Выбрать соответствующий условию задачи. Рассмотреть два вида движения: по суше и по воде. Использовать имеющиеся знания по классификации направления движения. Уточнить движение по воде с течением и в стоячей воде. Дать задание группам детального рассмотрения различных видов движения – каждая группа презентует один вид движения. При рассмотрении задач на работу напомнить о соотношении между объемом выполненной работы, затраченного времени и скоростью выполнения (производительность труда) (ввести формулу П=О/В) Рассмотреть случай, когда объем работы принята за 1. Соотношение: объем работы за единицу времени=1/затраченное время. Рассмотреть формулу совместной работы. 1/(t1 + t2 )=1/t1 +1/t2 Для рассмотрения решения задач на смеси и сплавы обеспечить предварительное повторение ключевых задач на проценты и части. Каждый урок завершить индивидуальным самостоятельным решением базовой задачи. На следующем уроке создать условия для само и взаимооценивания. Четвертый урок-обобщение темы решения текстовых задач. При делении на группы использовать деление выбором текста задачи вслепую, с последующим решением задачи в группах. Решение задач в группах, продумать игровые моменты, обеспечить взаимооценивание между группами. Продумать вопросы рефлексии для каждого урока по каждому типу задач. |
| 30 урок Урок обобщения и коррекции.
| Вопросы для развития навыков. Знание, понимание, применение. Вопросы по повторению Какие уравнения называются биквадратными? Какие уравнения называются дробно-рациональными? Что такое посторонние корни? Расскажите алгоритм решения дробно-рациональных уравнений. Алгоритм решения уравнений методом замены переменных. Этапы решения текстовых задач. Схема решения текстовых задач.
Анализ и оценка. Найдите ошибки и обоснуйте ответ в решении данных уравнений. Решите задачи с полным анализом решения.
| Групповая работа. Диалогическое обучение. Критериальное мышление. Взаимооценивание. Самооценивание. Рефлексия. Групповая работа - деление на группы случайным образом. Мобилизующее начало-математический диктант по вопросам раздела, в ходе диктанта повторить решение уравнений методом замены переменных и дробно-рациональных уравнений. Групповое задание- разделить по группам задания на решение уравнений методом замены переменных, дробно-рационального уравнения, текстовых задач на движение по воде и работу. Ввести критерии полного освещения вопроса на примере одного задания. Создать новые группы по выбору учеников для коррекции имеющихся пробелов. Организовать работу консультационной группы из числа продвинутых учеников. Продумать листы самооценивания по тематике разделов с четкими критериями. Соответственно самооцениванию осуществить выбор домашнего задания для коррекции перед итоговой контрольной работой. . |
| 31 урок Контрольная работа
| Контроль и оценка усвоения ЗУН по теме.
| Работа на 4 варианта, 5 заданий. 1-3 обязательный уровень, решение биквадратного уравнения, дробно-рационального – уравнения, текстовой задачи 4- средний уровень-решение уравнения на метод замены переменных 5 –высокий уровень- текстовая задача в измененных ситуациях. 6 – задание повышенной сложности (необязательное) Оценивание по критериям.
|

 Получите свидетельство
Получите свидетельство Вход
Вход



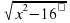 =3
=3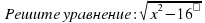 =3
=3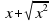 – 6=0
– 6=0








 Среднесрочный план по алгебре "Квадратные уравнения" (46.17 КB)
Среднесрочный план по алгебре "Квадратные уравнения" (46.17 КB)
 0
0 1323
1323 112
112 Нравится
0
Нравится
0


