Квадратные уравнения

В презентации приведены формулы и примеры решения разных видов квадратных уравнений. А так же частные случаи неполных квадратных уравнений и особые случаи. Показано решение задачи знаменитого индийского математика XІІ века Бхаскары.

Квадратное уравнение — это уравнение вида aх²+ bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;

2. Имеют ровно один корень;

3. Имеют два различных корня.

Дискриминант

D = b²− 4ac.

1. Если D < 0, корней нет;

2. Если D = 0, есть ровно один корень;

3. Если D > 0, корней будет два.

Решение квадратных уравнений

Выполнили учителя Мкоу гимназии вятские поляны:

Гатауллина гульфия анасовна и малькова надежда васильевна

Какое уравнение называется квадратным?

Формула для вычисления дискриминанта.

Формулы для нахождения корней.

Определение неполного квадратного уравнения.

Решение неполных квадратных уравнений.

Теорема Виета .

Корни квадратного уравнения для чётного b.

Особые случаи.

Проверь себя.

Старинная индийская задача

Определение:

Квадратное уравнение — это уравнение вида

aх 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Квадратные уравнения можно условно разделить на три класса:

• Не имеют корней;
• Имеют ровно один корень;
• Имеют два различных корня.

0, корней будет два. " width="640"

Дискриминант

D = b 2 − 4ac.

• Если D
• Если D = 0, есть ровно один корень;
• Если D 0, корней будет два.

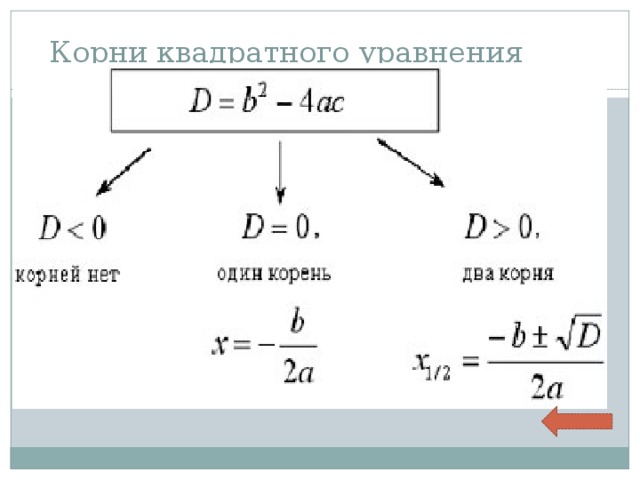
Корни квадратного уравнения

Неполные квадратные уравнения

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Решение неполных квадратных уравнений

Теорема Виета

• ax 2 +bx+c=0
• Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

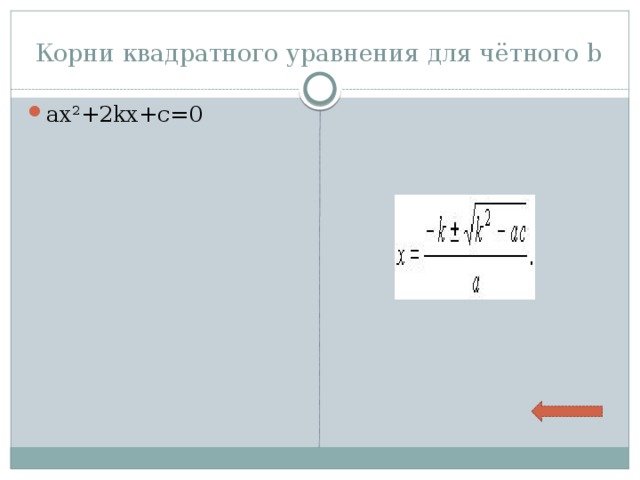
Корни квадратного уравнения для чётного b

• ax 2 +2kx+c=0

Особые случаи:

• ax 2 +bx+c=0

• ax 2 +bx+c=0
• если a + c = b , то х 1 = – 1, а х 2 =-c/a.

если a+b+c = 0, то

х 1 = 1, а х 2 =c/a .

Сколько корней имеют квадратные уравнения:

x 2 − 8x + 12 = 0;

5x 2 + 3x + 7 = 0;

x 2 − 6x + 9 = 0.

Решение

Выпишем коэффициенты для первого уравнения и найдем дискриминант: a = 1, b = −8, c = 12; D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение: a = 5; b = 3; c = 7; D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение: a = 1; b = −6; c = 9; D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Ответ1) 2 корня; 2) нет корней; 3) один корень.

Решить квадратные уравнения:

а)x 2 − 2x − 3 = 0;

б)15 − 2x − x 2 = 0;

в) x 2 + 12x + 36 = 0.

Решение

Решение:

Решение:

Решить неполные квадратные уравнения:

а)x 2 − 7x = 0;

б)5x 2 + 30 = 0;

в)4x 2 − 9 = 0.

Решение:

а)x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0;

x 2 = −(−7)/1 = 7.

б)5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

в)4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Ответ: а) x 1 = 0; x 2 = 7;

б) корней нет;

в) x 1 = 1,5; x 2 = 1,5.

Решите уравнения

2х²-5х+3=0 4х²+7х+3=0

3х²+4х-7=0 2х²-5х-7=0

- 9х²+8х+1=0 -3х²+5х+8=0

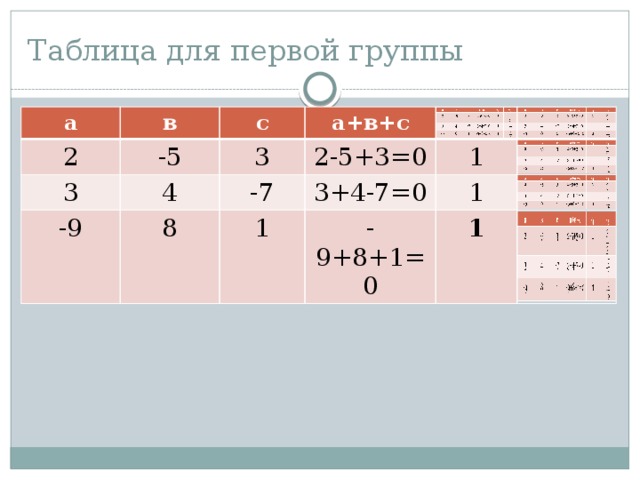
Таблица для первой группы

а

2

в

-5

3

с

а+в+с

3

4

-9

2-5+3=0

8

-7

1

3+4-7=0

1

-9+8+1=0

1

1

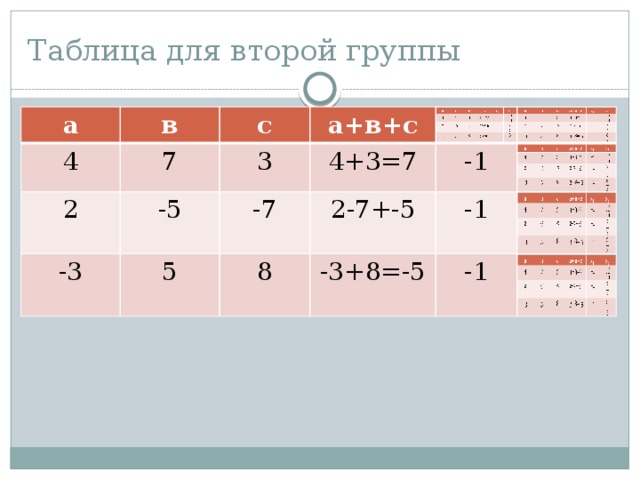
Таблица для второй группы

а

4

в

7

2

с

а+в+с

3

-5

-3

4+3=7

5

-7

-1

2-7+-5

8

-3+8=-5

-1

-1

Одна из задач знаменитого индийского математика XІІ века Бхаскары

Обезьянок резвых стая

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась.

А двенадцать по лианам…

Стали прыгать повисая…

Сколько было обезьянок

Ты скажи мне, в этой стае?.

Решение задачи Бхаскары

Успехов вам при решении квадратных уравнений