Данные об авторе
Автор(ы):
Климонова Галина Николаевна
Место работы, должность:
МАОУ СОШ №9 г. Тамбова, учитель математики
Регион:
Тамбовская область
Характеристики урока (занятия)
Уровень образования:
основное общее образование
Целевая аудитория:
Учитель (преподаватель)
Класс(ы):
8 класс
Тема урока: «Решение квадратных уравнений»
«Мне приходится делить своё время между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важнее, потому что
политика существует только до данного момента,
а уравнения будут существовать вечно».
А. Эйнштейн
Цель урока: обобщение, систематизация и закрепление знаний по теме «Решение квадратных уравнений»
Образовательные задачи урока:
систематизировать знания по теме;
расширить и углубить представления учащихся о решении уравнений;
формировать умения выбирать рациональный способ решения квадратных уравнений.
.Развивающие задачи урока:
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки;
развивать умения самостоятельной работы;
развивать устную и письменную речь учащихся;
развивать навыки самоконтроля и взаимоконтроля.
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
прививать интерес к математике.
формировать потребность добиваться успехов в приобретении знаний;
Тип урока:
Урок обобщения и систематизации знаний.
Формы обучения:
Индивидуальная, фронтальная работа, парная работа, взаимопомощь, групповая (коллективная) деятельность.
Список использованной литературы:
Алгебра: Учебник для 8 класса общеобразовательных учреждений / Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. – М.: Просвещение, 2011.
Алгебра: Учебник для 8 класса общеобразовательных учреждений под редакцией С. А. Теляковского. – М.: Просвещение, 2011.
А. П. Ершова, Голобородько В. В. Самостоятельные и контрольные работы для 8 класса. – М.: ИЛЕКСА, 2010.
А.Л Семенова, И.В. Ященко. ГИА 3000 задач, Москва «Экзамен» 2013г.
В.И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк. Дидактические материалы по алгебре для 8 класса. – М.: Просвещение, 2011.
Звавич Л. И., Рязановский А.Р.Алгебра.8 класс: Задачник для классов с углубленным изучением математики. М.: Мнемозина, 2009
М.В. Ткачева Тематические тесты Алгебра 8 класс Москва «Просвещение» 2010г
метод литерат
Алгебра. 8 класс поурочные планы по учебнику Ш. А. Алимова и др./ авт.- сост. Е. Г. Лебедева. – Волгоград: Учитель, 2009.
Г. И. Ковалева. Уроки математики в 8 классе. Поурочные планы. Часть 2.- Волгоград: Гринина Е. С.,2005.-64с.
Г.И. Глейзер «История математики в школе» (для учащихся 7-8 классов). Пособие для учителей. - М. Просвещение,1992
Математика. 5-8 классы: игровые технологии на уроках / авт.-сост. И.Б. Ремчукова. – Волгоград: Учитель, 2007.
Математика. 5-11 классы: уроки учительского мастерства / авт.-сост. Е.В. Алтухова и др. – Волгоград: Учитель, 2009.
Математика: Открытые уроки. 5,6, 7, 8, 9, 11классы. Вып. 2./ Авт.-сост. Н. М. Ляшева и др. – Волгоград: Учитель, 2005.
Математика.5-11 классы: игровые технологии на уроках / авт.-сост. Н.В. Барышникова. – Волгоград: Учитель, 2007.
Математика. 5-11 классы. Коллективный способ обучения: конспекты уроков, занимательные задачи / авт.-сост. И.В. Фотина. - Волгоград: Учитель,2009.
«Математика. Всё для учителя!» Учительский журнал.
С.Н. Олехник, М.К. Потапов, П.И. Пасиченко. Уравнения и неравенства (нестандартные методы решения) – М.: Просвещение, 2007.
Оборудование:
Компьютер, мультимедийная установка.
ЦОР
http://school-collection.edu.ru/catalog/res/54467594-eccb-4d4e-8039-4a73b6f69ca6/?interface=catalog
http://files.school-collection.edu.ru/dlrstore/5c9a9b61-b2d6-4be2-92bd-6748a14b8c8a/M22D2.swf
http://school-collection.edu.ru/catalog/res/c1162e51-0bdc-4ed6-9e94-0fddf33a0502/?interface=teacher&class=50&subject=17
http://fcior.edu.ru/card/3726/kvadratnoe-uravnenie.html
http://fcior.edu.ru/card/14481/reshenie-kvadratnyh-uravneniy-po-formule-k1.html
http://fcior.edu.ru/card/6769/reshenie-kvadratnyh-uravneniy-po-formule-p1.html
http://www.fcior.edu.ru/card/13512/kvadratnoe-uravnenie.html
Краткое описание ресурса:
Цель урока: обобщение, систематизация и закрепление знаний по теме «Решение квадратных уравнений»
Образовательные задачи урока:
систематизировать знания по теме;
расширить и углубить представления учащихся о решении уравнений;
формировать умения выбирать рациональный способ решения квадратных уравнений.
Развивающие задачи урока:
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки;
развивать умения самостоятельной работы;
развивать устную и письменную речь учащихся;
развивать навыки самоконтроля и взаимоконтроля.
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
прививать интерес к математике.
формировать потребность добиваться успехов в приобретении знаний;
Урок позволяет обобщить, систематизировать и закрепить знания по теме «Решение квадратных уравнений» и рассмотреть различные способы решения квадратных уравнений изучаемых на уроках алгебры в разное учебное время.
Результатом деятельности учащихся на уроке является понимание сути различных способов решения квадратных уравнений.
На уроке созданы условия для реализации основных принципов личностно ориентированной технологии обучения.
Учебная деятельность, организованная на уроке, способствует сохранению здоровья детей.
ПОЛНОЕ ОПИСАНИЕ
Тема урока: «Решение квадратных уравнений»
Сл.1
«Мне приходится делить своё время между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важнее, потому что
политика существует только до данного момента,
а уравнения будут существовать вечно».
А. Эйнштейн
Сл.
В течение урока используется слайдовая презентация.Ход урока:
Организационный момент.
Приветствие учителя. Проверка готовности к уроку.
Обращение внимания детей на эпиграф к уроку. Объявление темы и постановка задач урока.
Сл.
Актуализация знаний
На экране - уравнение: 15х2+12х+2012=0.
Сл.
Определите вид данного уравнения. Назовите его коэффициенты.
О каком событии говорят коэффициенты уравнения? (Дата проведения урока).
Откройте тетради и запишите сегодняшнее число, классная работа.
Фронтальная работа с классом.
Сл.
Какие уравнения называются квадратными?
Как вы считаете, на какой из коэффициентов накладывается ограничение и почему?(а 0)
0)
Всегда ли имеет корни квадратное уравнение? (Нет, не всегда)
От чего зависит количество корней? (От дискриминанта)
Как найти дискриминант квадратного уравнения? (D = b2 – 4ас)
Сколько корней имеет квадратное уравнение, если D 0 ?
Сколько коней имеет квадратное уравнение если D=0 ?
Сколько корней имеет квадратное уравнение, если D
Как найти корни квадратного уравнения? (х1,2 = 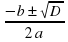 )
)
Итак, ребята, мы повторили основные понятия и формулы для решения квадратных уравнений.
На экране записаны уравнения:
Сл.
x2 + 9x – 12 = 0;
4x2 + 1 = 0;
x2 –2x + 5 = 0;
2z2 – 5z + 2 = 0;
4y2 = 1;
–2x2 – x + 1 = 0;
x2 + 8x = 0;
2x2=0;
–x2 – 8x=1
2x + x2 – 1=0
| Вопросы учащимся | Примерные ответы |
| 1. Дайте определение квадратного уравнения | Уравнение вида ax2+bx+c=0, где a0, называется квадратным |
| 2.Назовите виды квадратных уравнений | - полное; - неполное; - приведенное |
| 3. Запишите номера приведенных квадратных уравнений, записанных на доске | 1,3, 7, 10 |
| 4. Запишите номера неполных квадратных уравнений, записанных на доске | 2, 3, 7, 8 |
| 5. Запишите номера полных квадратных уравнений, записанных на доске | 1, 3, 4, 6, 9, 10 |
| 6.По какому признаку мы можем отнести квадратное уравнение к тому или иному виду? | В зависимости от коэффициентов уравнения. |
| 7. Как называются коэффициенты квадратного уравнения? | a – первый коэффициент, b – второй коэффициент, c – свободный член |
| 8. Запишите квадратное уравнение, у которого свободный член равен 6, первый коэффициент равен 1, а второй, равен –12. Как оно называется? | x2-12x+6=0 |
| 9. От чего зависит количество корней квадратного уравнения? | От знака дискриминанта. |
| 10. Впишите вместо пропуска такой коэффициент, чтобы квадратное уравнение 2х2–8х+....=0 не имело корней | 2х2–8х+9=0 (могут быть числа, больше, либо равные 9) |
| 11. Изменятся ли корни уравнения 2x2 +5x +7=0, если у него изменить знак: - одного коэффициента - трёх коэффициентов |
да нет |
| Как найти дискриминант квадратного уравнения? | D = b2 – 4ас) |
| Сколько корней имеет квадратное уравнение, если D 0 ? |
|
| Сколько коней имеет квадратное уравнение если D=0 ? |
|
| Сколько корней имеет квадратное уравнение, если D
|
|
| Как найти корни квадратного уравнения? | х1,2 = 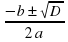 |
Сл.
Сегодня на уроке мы должны научиться выбирать рациональный способ решения квадратных уравнений.
Девизом нашего урока станут слова Рене Декарта: «Для разыскания истины вещей - необходим метод».
Сл.
Перед вами уравнения.
3x2-2x-5=0
X2=5
7x2+14x=0
X2+5x+4=0
X2+4x+4=0
X2-4=0
2x2-11x+5=0
X2+2x=x2+6
Сл.
Ваша задача - указать, какое из них рациональнее решить указанным мной способом. Если ответ верный, то откроется буква, соответствующая номеру этого уравнения и мы узнаем имя математика, который занимался изучением уравнений.
1)Какое уравнение решается вынесением общего множителя за скобки? №3 (Д)
2)Какое уравнение можно решить, методом выделения полного квадрата? №5 (И)
3) Какое уравнение решается по формуле, используя четный второй коэффициент?
№1 (О)
4)Какое уравнение удобно решить по теореме Виета?
№4 (Ф)
5)Какое уравнение можно решить разложением разности квадратов на множители?
№6 (А)
6)В каком уравнении надо применять общую формулу корней квадратного уравнения?
№7 (Н)
7)Какое уравнение можно решить извлечением квадратных корней? №2 (Т)
Имя математика, который занимался изучением уравнений, их классификацией, способами решения – Диофант.
Сл.
Как, не решая уравнения, узнать, имеет ли уравнение корни?
(Ученики отвечают: «Если а и с с противоположными знаками, то квадратное уравнение всегда имеет действительные корни».)
Решим квадратное уравнение 3х2 +2х-1=0.
Вспомним все способы, которые уже знаем.
1 способ. «По общей формуле, через дискриминант».
Используя общую формулу корней квадратного уравнения, решите его.
Ученики решают в тетради:
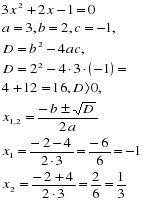
Все решили квадратное уравнение. Получили ответ.
Сл.
Перед вами лежат карточки (цифры 1, 2, 3, 4).Поднимите карточку с номером правильного ответа.
Кто поднял цифру 3 , то в лист учета знаний поставьте в 1 колонке знак «+». Молодцы!
Назовите коэффициенты квадратного уравнения.
(Ученики отвечают: а=3,в=2,с= -1.)
По какой формуле можно быстрее решить это квадратное уравнение?
(Ученики отвечают: «… по формуле с четным
коэффициентом при х»)
Способ №2.«С помощью формулы корней квадратного уравнения с четным вторым коэффициентом».
Решите квадратное уравнение 3х2+2х-1=0 с помощью формулы корней квадратного уравнения с четным вторым коэффициентом.
Ученики решают в тетрадях: 3х2+2х-1=0, к=1,
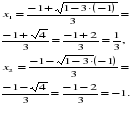
Проверка.
Сл.
Поменяйтесь тетрадями. Если решение правильное, в тетради поставьте знак «+» и в лист учета знаний в колонке № 2 знак «+».
Молодцы!
(Ученики проверяют и оценивают работу друг друга.)
Работа в группах.
На листочках написан способ, которым вы должны решить квадратное уравнение и затем защитить своё решение.
Ученики вытягивают листы, с указанным способом. Группой работают в тетрадях. Объясняют, проговаривают друг другу. Выбирают выступающего, который разъясняет, как решать квадратное уравнение этим способом.
Способ № 3.«Разложение левой части уравнения на множители способом группировки».
Способ № 4.« По сумме коэффициентов квадратного уравнения».
Способ № 5.« Решение уравнения, используя теорему, обратную теореме Виета».
Способ № 6.« Метод выделения полного квадрата».
Способ № 7.« Разложение квадратного трехчлена на множители».
Закончили решение.
Если вы владеете методом, над которым работала ваша группа, то в лист учета знаний поставьте знак «+», в колонке № 3.
Разбираем способы решения, остальные группы пишут в тетрадях.
Идет защита, остальные учащиеся пишут с доски в тетрадь.
Представитель каждой группы рассказывает о своем методе решения данного уравнения.
1 группа.
Способ № 3. «Разложение левой части уравнения на множители способом группировки».
Защита: 3х2+2х-1=0.
Представим слагаемое 2х в виде разности 3х-х. Разложим левую часть на
множители:
3х2+2х-1= 3х2+3х-х-1= 3х(х+1)+(-х-1)= 3х(х+1)-1(х+1)=(х+1)(3х-1)
Следовательно, уравнение можно записать так: (х+1)(3х-1)=0.
Произведение равно нулю, если хотя бы один из множителей равен нулю, а
другой при этом определен.
х+1=0 или 3х-1=0,
х=-1. 3х=1,
х=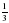 .
.
Левая часть уравнения обращается в нуль при х=-1;х=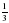 .
.
Значит, числа – 1 и 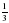 - корни уравнения 3х2+2х-1=0.
- корни уравнения 3х2+2х-1=0.
Сл.
Молодцы! Кто защищал этот способ, в лист учета знаний поставьте «!».
Способ № 4.« По сумме коэффициентов квадратного уравнения».
Если в квадратном уравнении ах2+вх+с=0, сумма коэффициентов а-в+с=0, то х1=-1, х2=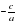 .
.
3х2+2х-1=0, а=3,в=2,с= -1, а-в+с =3-2+(-1)=0, значит х1=-1,
х2=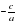 , х2=
, х2= =
=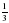 .
.
Ответ: – 1; 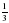 .
.
Молодцы!
Сл.
Физминутка.
Способ № 5.« Решение уравнения с применением теоремы, обратной теореме Виета».
Защита.
3х2+2х-1=0.
Разделим каждое слагаемое на 3. Приведенное квадратное уравнение будет иметь вид: 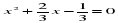 .
.
По теореме, обратной теореме Виета: если сумма двух чисел равна второму коэффициенту приведенного квадратного уравнения, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями приведенного квадратного уравнения.
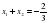 ,
,
 .
.
Если свободный член g - приведенного квадратного уравнения отрицателен, g= -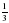 , то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет, отрицателен, так как
, то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет, отрицателен, так как 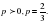
х1=-1, х2=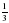 .
.
Сл.
Способ № 6.«Метод выделения полного квадрата».
Защита.
3х2+2х-1=0,
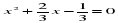 ,
,
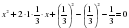 ,
,
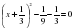 ,
,
 ,
,
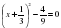 ,
,
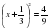 ,
,
 или
или 



 .
.
Способ № 7. « Разложение квадратного трехчлена на множители».
Защита.
Разложим квадратный трехчлен на множители. Для этого 3х2+2х-1=0 разделим на х+1.

- х -1
- х- 1
0
3(х+1)(3х-1)=0,
(х+1)(3х-1)=0,
Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом определен.
х+1=0 или 3х-1=0,
х= -1. 3х=1,
Х =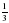 .
.
Сл.
Физминутка.
Способ №8. «Графическое решение квадратного уравнения».
Защита.
3х2+2х-1=0.
В уравнении второй и третий член перенесем в правую часть, то получим 3х2 =-2х+1.
Построим графики зависимостей у=3х2 и у=-2х+1. График первой зависимости -парабола, проходящая через начало координат. Так как коэффициент равен 3, то ветви параболы направлены вверх.
Учащиеся смотрят на слайд.
Сл.
График второй зависимости - прямая.
Прямая и парабола пересекаются в двух точках А и В с абсциссами х1=-1 и х2=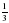 .
.
Учащиеся работают в листах учета знаний.
Сегодня на уроке мы с Вами разобрали 8 способов решения одного квадратного уравнения. Возьмите лист учета знаний, в колонке №5 поставьте цифру - сколько способов решения уравнения вам понятны, вы бы могли ими решить уравнения самостоятельно.
Сл.
Одно и то же уравнение может быть решено разными способами.
Домашнее задание.
Сл.
Учащиеся пишут в дневник.
Итог урока. Выставление оценок.
Подведем итоги урока.
Работая в группах. Составьте синквейн на тему: урок, уравнение, работа в группе, способы, восьмиклассники.
Учащиеся составляют, а потом зачитывают:
Урок
Необычный, увлекательный
Думаем, решаем, общаемся
Я умею решать уравнения
Интересно
Работа в группе
Весело, увлекательно
Решать, обсуждать, помогать
Мне нравиться так учиться
Мы вместе
Рисуют в листах учета свои эмоции: ☺.
Сл.
Сдают листы учета знаний учителю.
Вашим девизом должны стать слова: «Научился сам, научи другого!»
Сл.
Лист учета знаний.
8Б класс
| Способы решения квадратных уравнений |
-
| -
| -
| Защита | Самооценка | Итог |
|
|
|
|
|
|
|
![]() 0)
0)
 Получите свидетельство
Получите свидетельство Вход
Вход


 0)
0)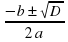 )
)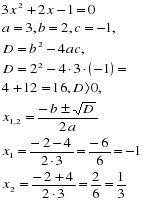
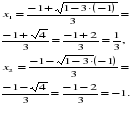
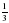 .
.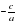 .
. =
=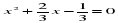 .
.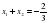 ,
, .
.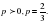
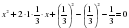 ,
,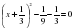 ,
, ,
,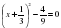 ,
,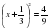 ,
,








 Решение квадратных уравнений (84.15 КB)
Решение квадратных уравнений (84.15 КB)
 0
0 669
669 34
34 Нравится
0
Нравится
0


