Государственное учреждение образования
«Средняя школа №5 г.Витебска»

Подготовила:
учитель математики
высшей категории
Кожемякина Е.С.
Кто с детских лет
занимается математикой,
тот развивает внимание,
тренирует свой мозг, свою
волю, воспитывает
настойчивость и упорство в
достижении цели.
А .Маркушевич
ЦЕЛИ:
теме;
интереса и математических
способностей,
сообразительности, логического
мышления;
непрерывному
совершенствованию своих
знаний.
Ход занятия:
1.Организационный момент
2.Проверка творческого задания «белка»
3.Устная работа
4. Стихотворение «Теорема
Виета»
5.Выполнение тестовых
заданий
6. Решение заданий повышенной сложности
7.Рефлексия

1.Сообщение учителем темы и целей занятия.
2. Проверка творческого задания «Белка».
Сейчас мы проверим творческое задание. Вам нужно было решить квадратные уравнения, корни которых являются координатами точек на координатной плоскости.
В результате верно выполненного задания у вас на плоскости получится изображение белки.

3. Устная работа на уроке: к каждому уравнению подберите пару чисел, являющихся корнями и покажите соответствие стрелкой
�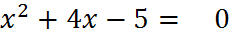 � -5; 9;
� -5; 9;
�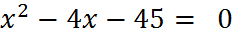 � -11;3;
� -11;3;
�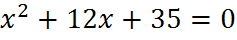 � 5;3
� 5;3
�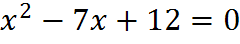 � -6;5
� -6;5
�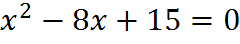 � -5;1
� -5;1
�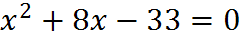 � -6;-5
� -6;-5
�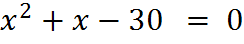 � 3;4
� 3;4
�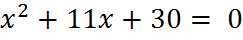 � -5;-7
� -5;-7
! При выполнении этого задания
вы использовали теорему, обратную
теореме Виета. Сформулируйте эту теорему.
4. Учитель: - Давайте послушаем стихи посвящённые теореме Виета, читает
Д.Семёнов. Автор И.Дырченко.
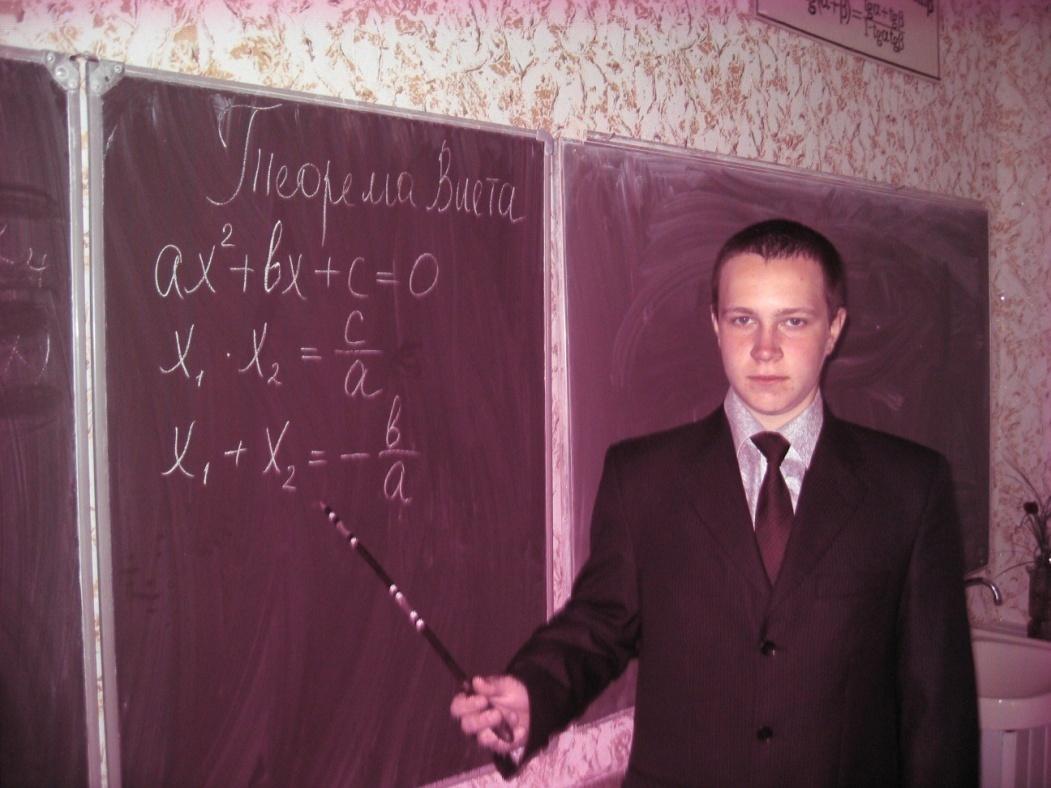
Теорема Виета
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого,
Умножишь ты корни - и дробь уж готова:
В числителе b в знаменателе а,
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта,
Что за беда-
В числителе b , в знаменателе а.
5. Тестовые задания
№1 Не решая уравнения �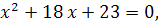 �
�
определите знаки его корней �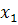 �и�
�и�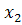 � (�
� (�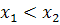 �)
�)
a)�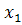 �0,�
�0,�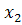 �0 b)�
�0 b)�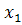 �0,�
�0,�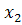 �0 б)�
�0 б)�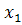 �0,�
�0,�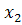 �0; г) �
�0; г) �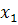 �0,�
�0,�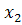 �0 д) иной ответ
�0 д) иной ответ
№2 При каких значениях k уравнение � � ,будет иметь два различных корня?
� ,будет иметь два различных корня?
а)k 0; б)k0; в)k≥ 0;
г)k = 0 д) иной ответ.
№3 При каких значениях k уравнение k=� � будет иметь два различных корня ?
� будет иметь два различных корня ?
а)k 0; б)k0; в)k≥ 0;
г)k = 0 д) иной ответ.
№4 При каких значениях k уравнение � � не будет иметь корней?
� не будет иметь корней?
а)k 4; б)k; в)k≥ -4;
г)k = -4; д) иной ответ.
№5 В каком случае верно указаны корни уравнения ?
а) � � �
� � � �
� � �;
�;
б) � � �
� � � �
� � �
�
в) � � �
� � � �
� � �
�
г)� � �
� � � �
� � �
�
д) иной ответ.
№6 Дано квадратное уравнение m� �+nx=0 относительно x. Укажите его корни. а) 0;--�
�+nx=0 относительно x. Укажите его корни. а) 0;--� �; б) 0; в)0;�
�; б) 0; в)0;� � г)0;�
� г)0;� � д) иной ответ.
� д) иной ответ.
Гимнастика для глаз

 8 ∞
8 ∞
Рисуй глазами треугольник.
Теперь его переверни вершиной вниз
И вновь глазами ты по периметру веди
Рисуй восьмерку вертикально
И головою не крути,
А только взглядом осторожно
Ты вдоль по линии води
И на бочок её клади
Теперь следи горизонтально
И в центре ты остановись
Зажмурься крепко, не ленись
Глаза открыли, наконец
Зарядка кончилась, ты молодец!
6.Задания повышенной сложности
№1. Решить уравнение
1)IxI∙ x+5x-6=0;
2)� � IxI-5=0;
� IxI-5=0;
3) (��
№2. Составить квадратное уравнение, корнями, которого являются числа � �+2 и�
�+2 и� �-2
�-2
№3. Решить уравнение относительно x
� � - 5ax+6�
� - 5ax+6� �=0.
�=0.
7. Рефлексия.
Вот и подошло к концу наше занятие.
- В руку я беру мелок
Вместе подведем итог.
Нарисуйте на карточке один из знаков ! ? —
! Всё понятно нам
«Ура» - восклицает детвора.
? У меня вопрос возник,
Что-то в тему я не вник!
— Чтобы в задачах таких разбираться,
Надо нам с вами еще заниматься.
Для учащихся, нарисовавших на карточке ? и – проводятся индивидуальные консультации.

 Получите свидетельство
Получите свидетельство Вход
Вход













 Квадратные уравнения (2.97 MB)
Квадратные уравнения (2.97 MB)
 0
0 651
651 49
49 Нравится
0
Нравится
0








