«Конус и его элементы» 11 класс

Конус и его элементы

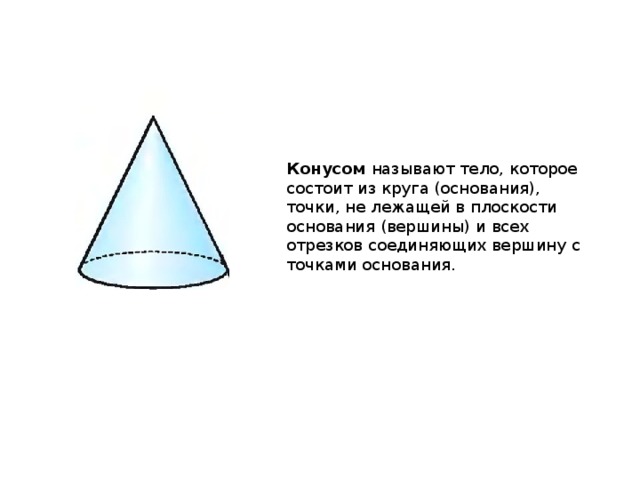
Конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.

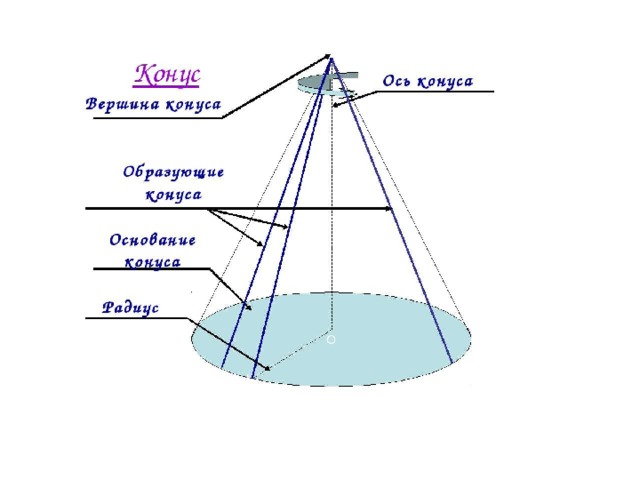
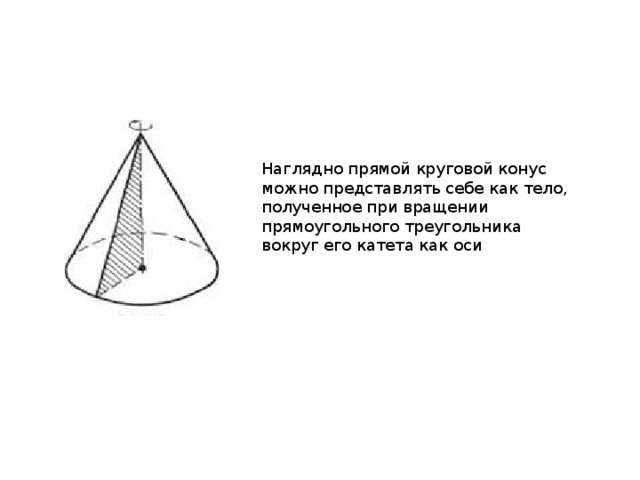
Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси

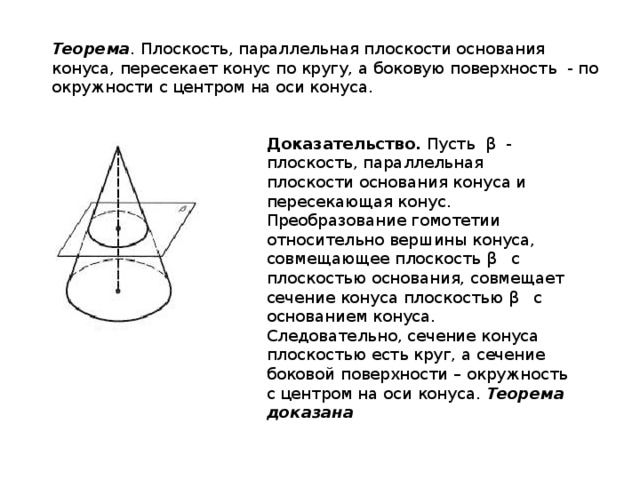
Теорема . Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность  - по окружности с центром на оси конуса.

Доказательство.  Пусть  β  - плоскость, параллельная плоскости основания конуса и пересекающая конус. Преобразование гомотетии относительно вершины конуса, совмещающее плоскость β   с плоскостью основания, совмещает сечение конуса плоскостью β   с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса.  Теорема доказана

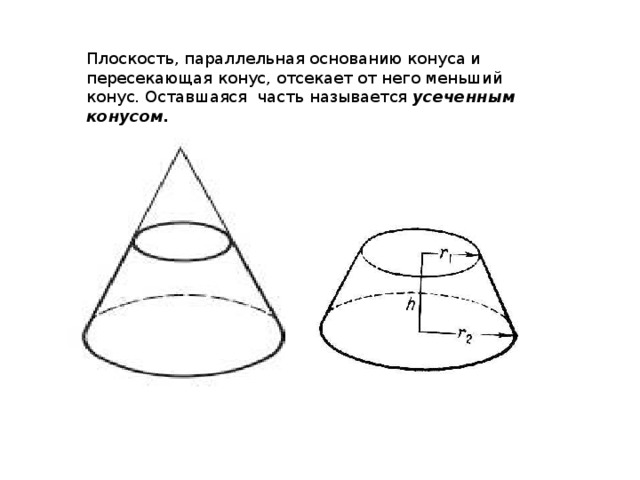
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся  часть называется  усеченным конусом.

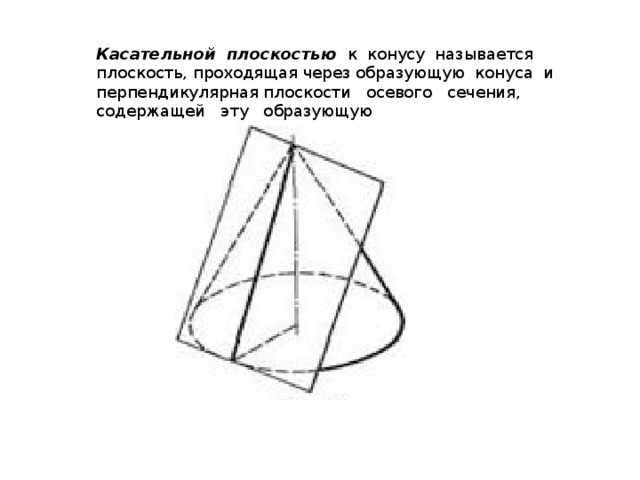
Касательной  плоскостью   к  конусу  называется  плоскость, проходящая через образующую  конуса  и  перпендикулярная плоскости   осевого   сечения,   содержащей   эту   образующую

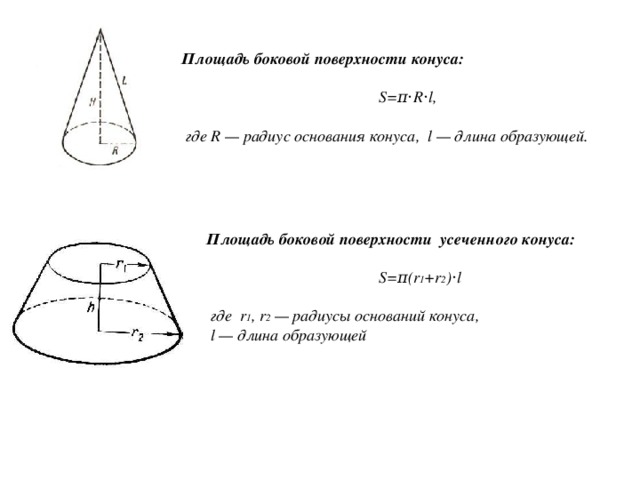
Площадь боковой поверхности конуса:

S=π⋅R⋅l,

где R — радиус основания конуса,  l — длина образующей.

Площадь боковой поверхности усеченного конуса:

S=π(r 1 +r 2 )⋅l

где  r 1 , r 2  — радиусы оснований конуса,

  l — длина образующей