Цель урока:
ознакомить учащихся с конусом и его элементами ;
рассмотреть сечение;
научить решать задачи;
Задачи урока:
Развивать логическое и пространственное мышление учащихся;
Познакомить учащихся с новым геометрическим телом;
Развивать умение анализировать, научить применять теоретические знания в практике;
Воспитывать трудолюбие, самостоятельность, любовь к предмету.
Типа урока: урок изучения нового материала с применением информационных технологий.
Форма урока: комбинированный урок.
Оборудование урока: компьютер, программный диск, модели конуса, картина Шишкина « Корабельная роща».
Ход урока
1. Изучение нового материала.
Ребята, как вы думаете какая связь между картиной Шишкина «Корабельная роща» и вот этим телом? (Демонстрируется модель конуса).
Оказывается самая непосредственная. На картине изображены сосны, а модель которую я держу называется конусом, что в переводе с греческого означает «сосновая шишка».
Вам знакомо понятие конуса, но сегодня мы должны дать строгое математическое определение данному телу, затем рассмотреть его свойства.
Где вы встречались с телами подобными конусу? (вопрос к классу).
Примеры: насыпанные на горизонтальной поверхности кучи песка, зерна, угля имеют форму конусов.
При этом каждому сыпучему материалу соответствует определенный угол укоса, так например,
песку - 25˚ щебню - 33˚
глине - 30˚ углю - 42˚.
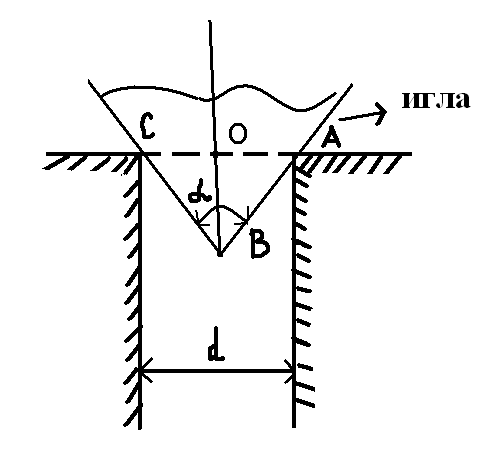
Другие примеры, нижняя часть углубления сделанная сверлом в металле,
верхние части нефтехранилищ и т. д.
Итак, что же называется конусом.
- Вводится понятие конической поверхности, образующих коническое поверхности.
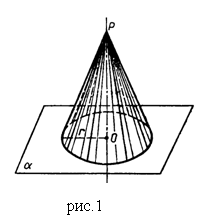
- Определение конуса: Тело, ограниченное коническое поверхностью и кругом с
границей называется конусом. (рис. 1)
Коническая поверхность называется боковой поверхностью конуса.
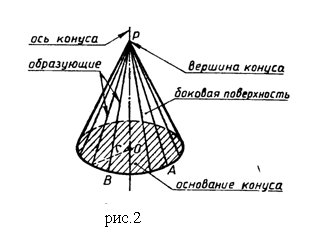
- Формируется определение высоты, радиуса, оси конуса, образующей. (рис. 2)
- Формируется определение прямого конуса.
- Конус называется прямым, если прямая соединяющая вершину с центром основания перпендикулярна плоскости основания.
В дальнейшем в школьном курсе будем рассматривать только прямые круговые конусы, для краткости называя конусом.
Есть у нас еще обобщенные конусы.
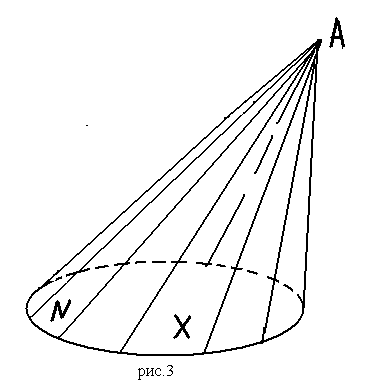
Обобщенный конус с основанием произвольной плоской фигурой
N и вершиной не лежащей в плоскости N точкой А - это фигура, которую заполняют отрезки АХ , соединяющие вершину со всеми точками оснований N.
Если N - круг - то круговой конус.
Если N - многоугольник - то пирамида ( «Энциклопедия юного математика» стр. 150)
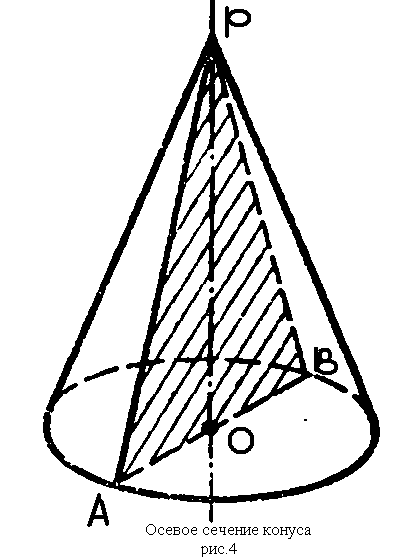
е) рассмотреть сечение конуса различными плоскостями.
Сечение конуса плоскостью, проходящей через его ось называется осевым сечением.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



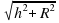

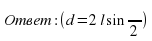









 Разработка урока по геометрии "Тела вращения. Конус" (0.12 MB)
Разработка урока по геометрии "Тела вращения. Конус" (0.12 MB)
 1
1 817
817 124
124 Нравится
0
Нравится
0


