Учебный лист по математике "Фигуры вращения. Цилиндр. Конус"

Дидактические материалы к урокам геометрии в 11 классе составлены по технологии индивидуализированного способа обучения (ТИСО), и представляют содержание:

учебного листа;

проверочных работ;

рейтингового листа.

В работе представлены уроки  по курсу «Геометрия - 11» по теме:

- Тела вращения. Цилиндр. Конус.

По программе на эту тему отведено 9 часов.

Модуль темы:

1,2 уроки – вводная лекция, в режиме УДЕ.

3,4 уроки – практикум по решению задач, традиционный метод решения задач.

5,6,7 уроки – практическая работа, отработка теоретического материала в режиме ТИСО по учебному листу с выполнением проверочных работ.

8 урок – обобщающий урок, коррекция.

9 урок – итоговая контрольная работа, контрольная работа № 2.

Мною отправляются   учебный лист к 5, 6 и 7 урокам, рейтинговый лист, проверочная работа №1, проверочная работа №2.

Материалы  помогут учителю организовать самостоятельную работу учащихся и осуществить целенаправленный контроль за состоянием знаний и умений учащихся по изучаемой теме.

УЧЕБНЫЙ  ЛИСТ

ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ:

В результате изучения темы нужно  знать:             

определение цилиндра и его элементов: основания цилиндра; радиус цилиндра; образующая цилиндра; высота цилиндра; 

определение конуса и его элементов: основание конуса; радиус конуса; образующая конуса; высота конуса;

определение усеченного конуса и его элементов: основания усеченного конуса; радиусы усеченного конуса; образующая усеченного конуса; высота усеченного конуса;

развертку и площадь боковой поверхности цилиндра, развертку и площадь полной поверхности цилиндра; 

развертку и площадь боковой поверхности конуса, развертку и площадь полной поверхности конуса;

развертку и площадь боковой поверхности усеченного конуса, развертку и площадь полной поверхности усеченного конуса;

виды цилиндра: прямой цилиндр, наклонный цилиндр; равносторонний цилиндр.

виды конуса: прямой конус, непрямой конус; усеченный конус.

сечения цилиндра: осевое сечение; сечение цилиндра, параллельное его оси; сечение цилиндра, перпендикулярное к его оси; сечение цилиндра плоскостью не пересекающей его основания и не перпендикулярной его оси;

сечения конуса: осевое сечение; сечение конуса, перпендикулярное к его оси; сечение конуса плоскостью не пересекающей его основания и не перпендикулярной его оси;

касательная плоскость цилиндра;

развертка цилиндра;

площадь боковой поверхности цилиндра; площадь полной поверхности цилиндра;

вписанный в призму цилиндр; описанный около призмы цилиндр;

В результате изучения темы нужно  уметь:

различать и показывать на моделях цилиндр, указывать их основные элементы  на    рисунке;

изображать на рисунках цилиндр;

выполнять чертежи по условиям задач;

решать задачи на нахождение геометрических величин (длин, углов, площадей);

решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур отношений между ними, применяя алгебраический и тригонометрический аппарат;

находить площади боковой и полной поверхностей цилиндра;

изображать сечения цилиндра плоскостью;

изображать цилиндр, вписанный в призму и описанный около призмы.

ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ:

владение государственным и родным языками;

проявление высокой культуры человеческого общения, соблюдение этических норм;

способность к самообразованию, саморазвитию, рефлексивному анализу собственной деятельности;

сформированность  мотивации к учению и познанию;

способность к решению практических задач на основе геометрических знаний и представлений о природе, знаковых и информационных системах;

умение контролировать процесс и результат учебной математической деятельности;

владение коммуникативными навыками в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой . других видах деятельности.

СИСТЕМНО-ДЕЯТЕЛЬНОСТНЫЕ РЕЗУЛЬТАТЫ:

владение законами логики математических рассуждений, их применение в различных областях человеческой деятельности;

умение использовать изученные формулы и свойства геометрических фигур для описания и исследования реальных объектов;

умение анализировать, обрабатывать, синтезировать и использовать научную информацию о свойствах плоских и пространственных геометрических фигур, о нахождении геометрических величин;

владение современными информационно-коммуникативными технологиями и полиязыковой культурой для поиска и обработки информации;

умение понимать и использовать геометрические модели и средства наглядности для иллюстрации, интерпретации и аргуменации проведенных исследований.

ЗАДАНИЕ №1

1) Прочитай в учебнике главу ІІ, § 5, пп. 5.1, 5.2, 5.3, 5.4.

(Геометрия. 11 класс. Кайдасов Ж., Хабарова Г., Абдиев А.. Алматы: Мектеп. 2011 г.)

2) Ответь на вопросы:

- какая фигура получится при вращении прямоугольника вокруг одной из его сторон? (1 балл)

- на рисунке изображен прямой круговой цилиндр:

а) укажите равные отрезки на рисунке (1 балл);

б) какой отрезок принадлежит оси цилиндра? (1 балл)

в) какой отрезок является высотой цилиндра? (1 балл)

г) какие отрезки являются образующими цилиндра? (1 балл)

Весь материал - в документе.

Работа представляет собой учебный лист по закреплению теории и отработке навыков решения задач по теме: «Фигуры вращения. Конус. Цилиндр.»

Дидактические материалы к урокам геометрии в 11 классе составлены по технологии индивидуализированного способа обучения (ТИСО), и представляют содержание:

• учебного листа;

• проверочных работ;

• рейтингового листа.

В работе представлены уроки по курсу «Геометрия - 11» по теме:

- Тела вращения. Цилиндр. Конус.

По программе на эту тему отведено 9 часов.

Модуль темы:

1,2 уроки – вводная лекция, в режиме УДЕ.

3,4 уроки – практикум по решению задач, традиционный метод решения задач.

5,6,7 уроки – практическая работа, отработка теоретического материала в режиме ТИСО по учебному листу с выполнением проверочных работ.

8 урок – обобщающий урок, коррекция.

9 урок – итоговая контрольная работа, контрольная работа № 2.

Мною отправляются учебный лист к 5, 6 и 7 урокам, рейтинговый лист, проверочная работа №1, проверочная работа №2.

Материалы помогут учителю организовать самостоятельную работу учащихся и осуществить целенаправленный контроль за состоянием знаний и умений учащихся по изучаемой теме.

УЧЕБНЫЙ ЛИСТ

по теме: ФИГУРЫ ВРАЩЕНИЯ. ЦИЛИНДР. КОНУС.

(3 занятия)

ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ:

В результате изучения темы нужно знать:

• определение цилиндра и его элементов: основания цилиндра; радиус цилиндра; образующая цилиндра; высота цилиндра;

• определение конуса и его элементов: основание конуса; радиус конуса; образующая конуса; высота конуса;

• определение усеченного конуса и его элементов: основания усеченного конуса; радиусы усеченного конуса; образующая усеченного конуса; высота усеченного конуса;

• развертку и площадь боковой поверхности цилиндра, развертку и площадь полной поверхности цилиндра;

• развертку и площадь боковой поверхности конуса, развертку и площадь полной поверхности конуса;

• развертку и площадь боковой поверхности усеченного конуса, развертку и площадь полной поверхности усеченного конуса;

• виды цилиндра: прямой цилиндр, наклонный цилиндр; равносторонний цилиндр.

• виды конуса: прямой конус, непрямой конус; усеченный конус.

• сечения цилиндра: осевое сечение; сечение цилиндра, параллельное его оси; сечение цилиндра, перпендикулярное к его оси; сечение цилиндра плоскостью не пересекающей его основания и не перпендикулярной его оси;

• сечения конуса: осевое сечение; сечение конуса, перпендикулярное к его оси; сечение конуса плоскостью не пересекающей его основания и не перпендикулярной его оси;

• касательная плоскость цилиндра;

• развертка цилиндра;

• площадь боковой поверхности цилиндра; площадь полной поверхности цилиндра;

• вписанный в призму цилиндр; описанный около призмы цилиндр;

В результате изучения темы нужно уметь:

• различать и показывать на моделях цилиндр, указывать их основные элементы на рисунке;

• изображать на рисунках цилиндр;

• выполнять чертежи по условиям задач;

• решать задачи на нахождение геометрических величин (длин, углов, площадей);

• решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур отношений между ними, применяя алгебраический и тригонометрический аппарат;

• находить площади боковой и полной поверхностей цилиндра;

• изображать сечения цилиндра плоскостью;

• изображать цилиндр, вписанный в призму и описанный около призмы.

ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ:

• владение государственным и родным языками;

• проявление высокой культуры человеческого общения, соблюдение этических норм;

• способность к самообразованию, саморазвитию, рефлексивному анализу собственной деятельности;

• сформированность мотивации к учению и познанию;

• способность к решению практических задач на основе геометрических знаний и представлений о природе, знаковых и информационных системах;

• умение контролировать процесс и результат учебной математической деятельности;

• владение коммуникативными навыками в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой . других видах деятельности.

СИСТЕМНО-ДЕЯТЕЛЬНОСТНЫЕ РЕЗУЛЬТАТЫ:

• владение законами логики математических рассуждений, их применение в различных областях человеческой деятельности;

• умение использовать изученные формулы и свойства геометрических фигур для описания и исследования реальных объектов;

• умение анализировать, обрабатывать, синтезировать и использовать научную информацию о свойствах плоских и пространственных геометрических фигур, о нахождении геометрических величин;

• владение современными информационно-коммуникативными технологиями и полиязыковой культурой для поиска и обработки информации;

• умение понимать и использовать геометрические модели и средства наглядности для иллюстрации, интерпретации и аргуменации проведенных исследований.

ПАМЯТКА.

Помни, что работать нужно по алгоритму!

Не забывай проходить проверку, делать пометки на полях, заполнять рейтинговый лист темы.

Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.

Будь объективен во время взаимопроверки, это поможет и тебе, и тому, кого ты проверяешь.

ЖЕЛАЮ УСПЕХА!

ЗАДАНИЕ №1

1) Прочитай в учебнике главу ІІ, § 5, пп. 5.1, 5.2, 5.3, 5.4.

(Геометрия. 11 класс. Кайдасов Ж., Хабарова Г., Абдиев А.. Алматы: Мектеп. 2011 г.)

2) Ответь на вопросы:

- какая фигура получится при вращении прямоугольника вокруг одной из его сторон? (1 балл)

- на рисунке изображен прямой круговой цилиндр:

а) укажите равные отрезки на рисунке (1 балл);

б) какой отрезок принадлежит оси цилиндра? (1 балл)

в) какой отрезок является высотой цилиндра? (1 балл)

г) какие отрезки являются образующими цилиндра? (1 балл)

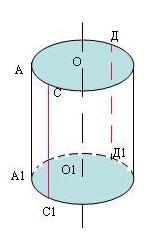
- Какая фигура получается в сечении цилиндра плоскостью:

а) параллельной оси цилиндра (1 балл);

б) параллельной основаниям цилиндра (1 балл)

в) не параллельной оси цилиндра (1 балл)

г) не параллельной основаниям цилиндра (1 балл)

- Какую форму имеет осевое сечение прямого цилиндра? (1 балл)

- Можно ли вращением произвольного параллелограмма вокруг одной из сторон получить цилиндр? (1 балл)

- Какая фигура получится при вращении прямоугольного треугольника вокруг одного из катетов? (1 балл)

- на рисунке изображен прямой круговой конус:

а) укажите равные отрезки на рисунке (1 балл);

б) какой отрезок принадлежит оси конуса? (1 балл)

в) какой отрезок является высотой конуса? (1 балл)

г) какие отрезки являются образующими конуса? (1 балл)

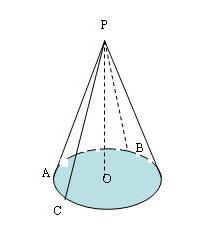
- Может ли образующая конуса равняться:

а) высоте конуса; (1 балл)

б) радиусу окружности основания? (1 балл)

- Есть ли у конуса центр, ось или плоскость симметрии? (1 балл)

- Может ли в сечении конуса плоскостью получиться равнобедренный треугольник, отличный от осевого сечения? (1 балл)

- Как нужно пересечь конус плоскостью, чтобы в сечении получился:

а) круг; (1 балл)

б) фигура, ограниченная эллипсом? (1 балл)

3) Правильно переставь слова в правом столбце (Работа с таблицей. Приложение 1)

ПРОЙДИ ПРОВЕРКУ №1

1. Рассмотри на примерах способы решения задач:

Пример 1. стр 33, №11. Дан цилиндр с радиусом основания 3 м и высотой 10 м. Найдите диагональ осевого сечения цилиндра.

Решение:

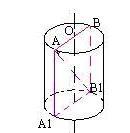
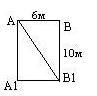
Дано:

Цилиндр.

R= 3 м, H= 10 м, AB₁- диагональ осевого сечения.

Найти:

AB₁

Так как прямоугольник AA₁B₁B является осевым сечением цилиндра, то

Δ AВB₁ - прямоугольный. По теореме Пифагора:

=; .

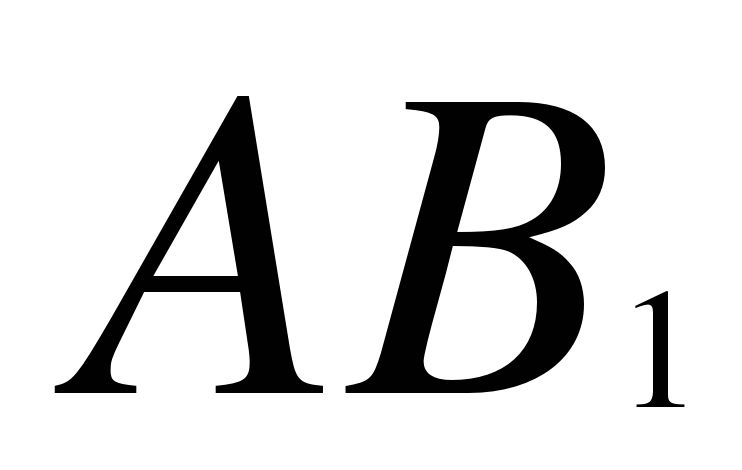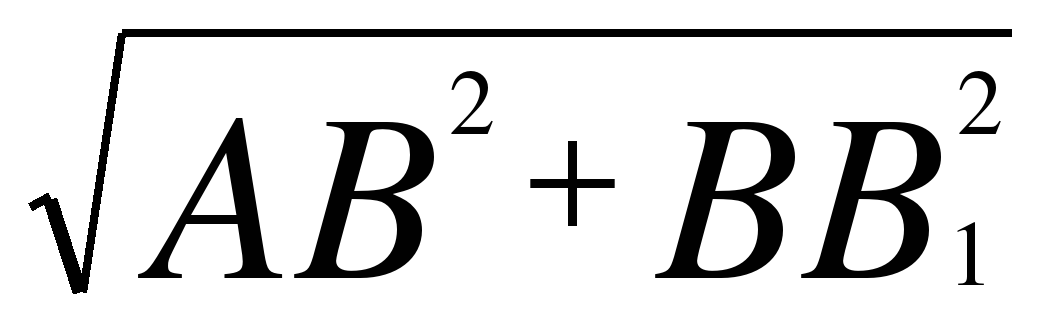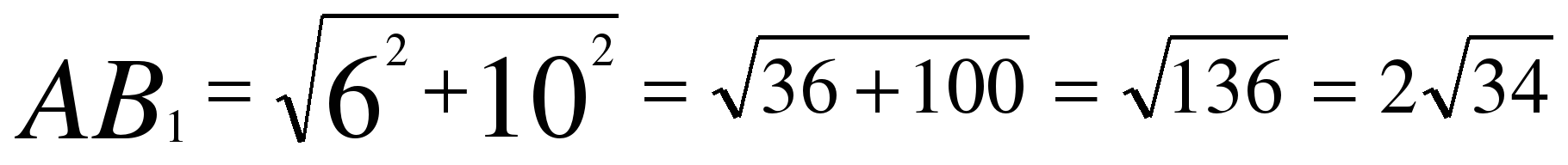Ответ: .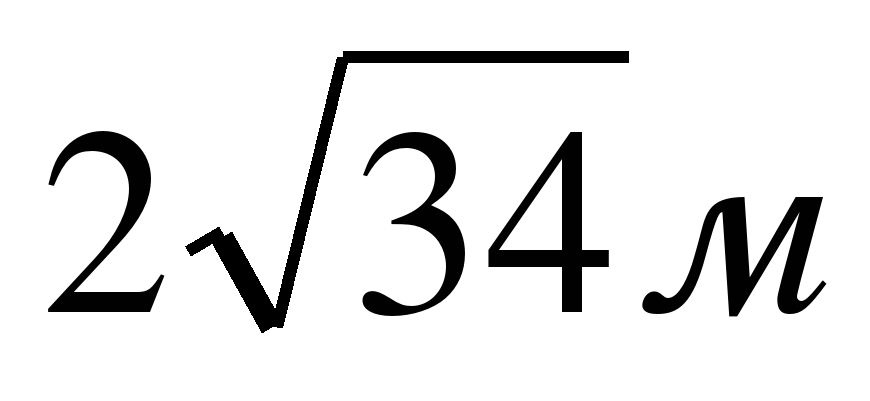

Пример 2. стр 33, №13. Высота цилиндра 8 см, диаметр основания 10 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.

Решение:

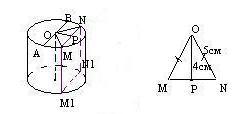
Дано:

Цилиндр.

D=10см, H= 8см, MM₁N₁N – сечение цилиндра, (MM₁N₁N)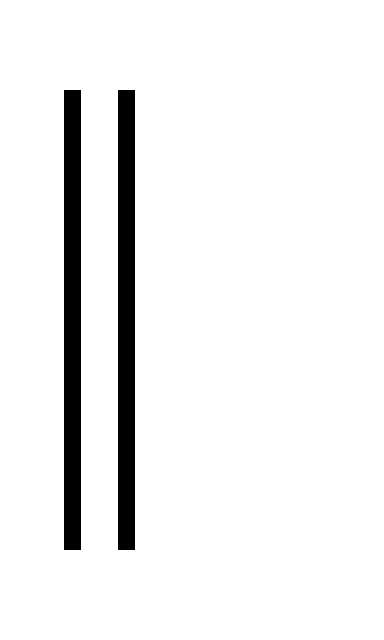ОО₁.

ОР = 4см, расстояние от оси цилиндра до сечения.

Найти: S_{сечения}

MM₁N₁N – прямоугольник. S_{сечения} = MM₁∙ MN

MM₁ = H=8см

Соединив точку О с точкой N и с точкой M, получим треугольник MON – равнобедренный, MN- основание, OM=ON=R=10׃ 2=5(см)

Треугольник OPN – прямоугольный (так как ОР - расстояние от оси цилиндра до сечения, то ОР 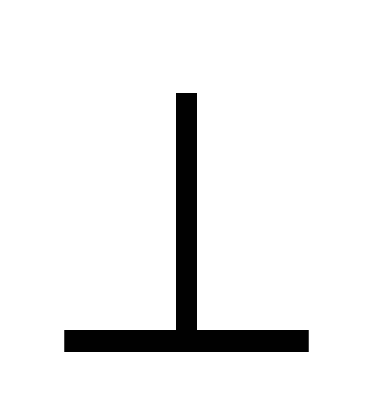MN):

PN=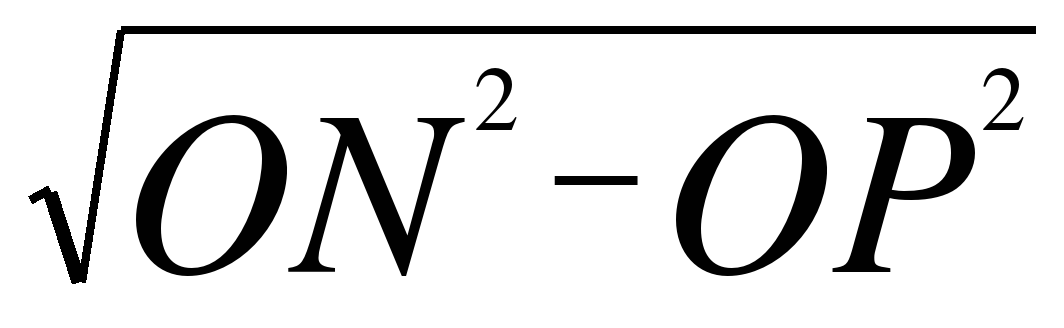==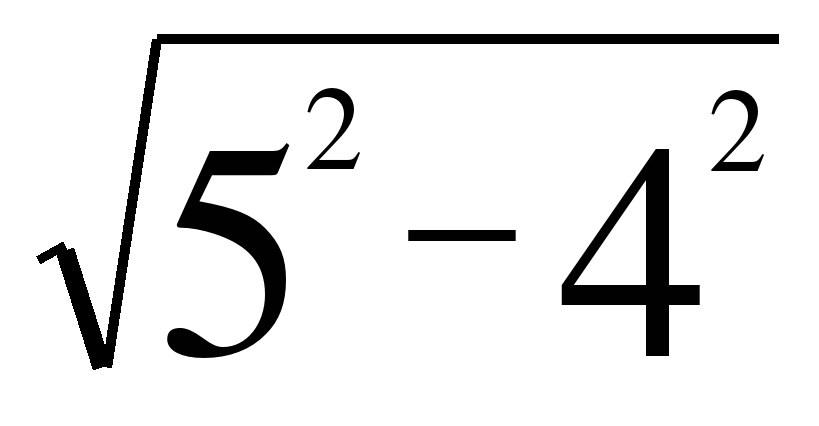==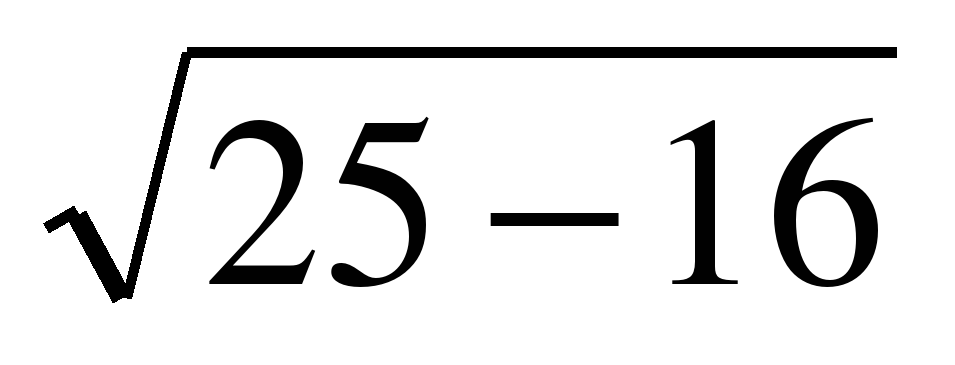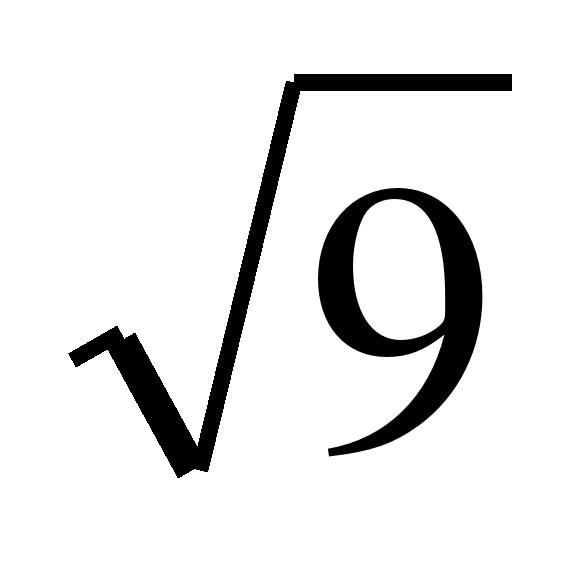3(см)

MN=2∙ PN, MN=2∙3=6(см)

S_{сечения} = 8∙ 6 = 48 (см²)

Ответ: 48 см²

Пример 3. стр 34, №24. Вычислите площадь поверхности цилиндра по следующим данным: 1) диаметр основания равен 12 см, высота – 3,5 см; 2) радиус основания 18 см, высота 2,5 дм.

Решение: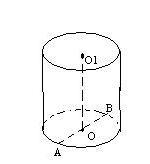

S_{бок пов цил} = 2πRH

1. R=D׃2=12׃2=6(см)

S_{бок пов цил} = 2π∙6∙3,5=42π (см²)

2) Н=2,5 дм =25см. S_{бок пов цил} = 2π∙18∙25=900π (см²)

Ответ: 1) 42π см²; 2) 900π см².

Пример 4. стр 34, №31.В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра если радиус основания равен высоте цилиндра.

Решение:

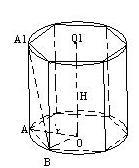
Цилиндр, в цилиндр вписана правильная шестиугольная призма.

АВ₁ - диагональ боковой грани призмы.

ОО₁ – ось цилиндра.

R_осн = H_цил

Найти:

АВ₁В

Боковая грань АА₁В₁В призмы является прямоугольником. Тогда треугольник АВВ₁ – прямоугольный.

Треугольник АОВ равносторонний, так как основание призмы правильный шестиугольник. Тогда АВ=R=H. Отсюда следует, что треугольник АВВ₁ – равнобедренный, то есть АВ₁В = 90⁰׃ 2 = 45⁰.

Ответ: 45⁰.

Пример 5. стр 43, № 9. Высота конуса равна 8 м, радиус основания 6м.

Найдите образующую конуса.

Решение:

Дано: Конус. H=8м, R=6м, SA- образующая.

Найти: SА

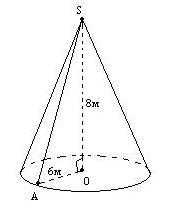Треугольник SOA – прямоугольный: по теореме Пифагора SA=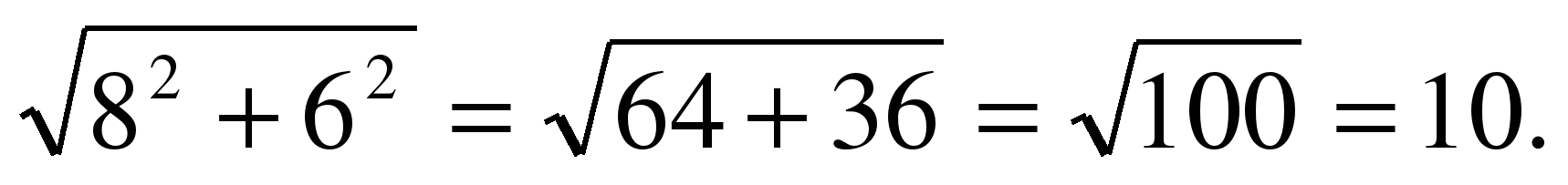

Ответ: 10м.

Пример 6. стр 43, №12. Радиус основания конуса r, его осевое сечение – прямоугольный треугольник. Найдите площадь сечения.

Решение:

Дано: Конус, r – радиус основания, ASB – прямоугольный, осевое сечение.

Найти: S_{сечения}

Так как катеты ASB являются образующими конуса, то он еще и равнобедренный. Поэтому S_{сечения} = . По теореме Пифагора: 2= =

. S_{сечения} =

Ответ: кв. ед.

Пример 7. стр 44, №24. Вычислите боковую и полную поверхности конуса, образующая которого равна 1,6 дм, а радиус основания – 4 см.

Решение:

Дано: Конус. SA- образующая, SA=1,6 дм, R= 4 см.

Найти: S_{бок пов кон} ; S_{пол пов кон}

S_{бок пов кон} = ; S_{бок пов кон} =

S_{пол пов кон} = ; S_{пол пов кон} =

Ответ: ; .

Пример 8. стр 45, №34. В конусе даны радиус основания R и высота Н. Найдите ребро вписанного в него куба.

Решение:

Дано: Конус. R- радиус основания, H- высота конуса. Куб вписан в конус. а- ребро куба.

Найти: а.

Треугольники _ подобные.

d –диаметр основания куба. _ ; _{ }

Из подобия треугольников: _{   }

_{  }

Ответ:_ .

ЗАДАНИЕ №2

Выборочно реши одну задачу: (2б)

1. стр 33, №12;

Дан цилиндр с радиусом основания 3 см, диагональ осевого сечения равна 10 см. Найдите: а) высоту цилиндра; б) площадь осевого сечения цилиндра.

стр43, №10

Образующая конуса равна 8 м и наклонена к плоскости основания под углом 60⁰. Найдите площадь основания конуса.

1. Реши на выбор три задачи: (6б)

а) стр 34, № 25.Стороны прямоугольника 4 см и 5 см. Найдите площадь поверхности тела, поученного при вращении этого прямоугольника вокруг меньшей стороны.

б)стр 34, № 32. Докажите, что в любой четырехугольной призме, описанной вокруг цилиндра, сумма площадей противоположных граней равна.

в) стр 44, № 24. Вычислите боковую и полную поверхности конуса, образующая которого равна 1,6 дм, а радиус основания – 4 см.

г) стр 45, № 33(б), Площадь боковой поверхности конуса Q, а его радиус r. Найдите длину бокового ребра вписанной в этот конус правильной четырехугольной пирамиды.

д) стр 46, № 41(а).Радиусы оснований усечен усеченного конуса равны 3 дм и 6 дм, а образующая – 5 дм. Найдите высоту усеченного конуса.

1. Реши на выбор три: (6б)

а) стр33, № 20. Отрезок одним из своих концов скользит по окружности, оставаясь перпендикулярным к ее плоскости. Какая фигура при этом получится?

б)стр 35, №35. Боковое ребро правильной треугольной пирамиды равно b и образует с плоскостью основания угол α. В пирамиду вписан равносторонний цилиндр так, что его нижнее основание лежит в плоскости основания пирамиды. Найдите высоту цилиндра.

в) стр 44, № 20.Дан конус, образующая которого равна l (англ.L мален), а радиус основания – R. При каком условии у данного конуса существуют две взаимно перпендикулярные образующие?

г)стр45, № 38. Площадь основания конуса равна q, угол при вершине осевого сечения – α. Найдите площадь полной поверхности правильной четырехугольной пирамиды, вписанной в конус.

д) стр 46, № 40. Какие размеры имеет развертка боковой поверхности ведра, если диаметры его оснований равны 28 см и 20 см, а высота – 24 см. Сколько квадратных диаметров материала нужно затратить на изготовление этого ведра (без учета расходов на швы)?

ПРОЙДИ ПРОВЕРКУ №2

ЗАДАНИЕ №3

Молодец! Можно приступить к проверочной работе №1.

ЗАДАНИЕ №4

1) Реши по одной задаче из А, В, С: (6б)

А

1. Разверткой боковой поверхности цилиндра является прямоугольник ABCD, AC=8СМ, CAD=30⁰. Найдите площадь полной поверхности цилиндра, если его высота равна AD.

2. Осевое сечение конуса – равнобедренный треугольник с углом 120⁰ и сторонами, равными 16 см. найдите площадь полной поверхности конуса.

В

1. Диагональ осевого сечения цилиндра равна 8_ см и образует с плоскостью основания угол 45⁰. Найдите площадь полной поверхности цилиндра.

2. Длины окружностей оснований усеченного конуса равны 4π и 10π. Высота конуса равна 4. Найдите площадь поверхности усеченного конуса.

С

1. В правильную треугольную призму вписан цилиндр. Найдите площадь его поверхности, если сторона основания призмы равна _, а высота – 3 см.

2. В правильной треугольной пирамиде сторона основания равна а, а боковые грани наклонены к плоскости основания под углом 45⁰. Найдите площадь боковой поверхности вписанного в пирамиду конуса.

ПРОЙДИ ПРОВЕРКУ №3

ЗАДАНИЕ №5

Проверь свои знания, выполнив проверочную работу №2.

Реши любые три задачи. (6 баллов)

ПРОВЕРОЧНАЯ РАБОТА №1

№1. Решите задачи, вариант А или В: (6б)

А

1. Радиус основания цилиндра – 3 см, высота – 8 см. найдите диагональ осевого сечения.

2. Радиус основания цилиндра в 3 раза меньше высоты, а площадь осевого сечения равна 24 см². Найдите размеры цилиндра.

3. Через образующую цилиндра проведено два сечения, из которых одно осевое с площадью, равной S. Угол между плоскостями сечений равен 30⁰. Найдите площадь второго сечения.

В

1. Диагональ осевого сечения цилиндра – 5 см, высота цилиндра – 3 см, найдите радиус основания.

2. Высота цилиндра на 10 см больше радиуса основания, а площадь осевого сечения равна 22см². Найдите размеры цилиндра.

3. Через образующую цилиндра проведено два сечения, из которых одно осевое. Площадь меньшего из сечений равна Q. Угол между плоскостями сечений равен 60⁰. Найдите площадь осевого сечения.

№2. Решите любые две задачи: (4б)

А

1. Радиус основания конуса – 5 см, высота – 12 см. найдите образующую.

2. Осевое сечение конуса – треугольник, площадь которого равна

16 _, а один из углов – 120⁰. Найдите радиус основания конуса.

1. Хорда основания конуса равна 6 см и стягивает дугу 90⁰. Высота конуса равна 4 см. найдите площадь сечения, проведенного через вершину конуса и данную хорду.

В

1. Образующая конуса длиной 10 см наклонена к плоскости основания под углом 30⁰. Найдите радиус основания.

2. Радиус основания конуса – 3 см. осевым сечением является прямоугольный треугольник. Найдите его площадь.

3. Высота конуса – 20 см, радиус его основания – 25 см. найдите площадь сечения, проведенного через вершину, если расстояние от центра основания до плоскости сечения равно 12 см.

ИТОГО: 10 баллов

«5» - 10б;

«4» - 8б;

«3» - 6б

ПРОВЕРОЧНАЯ РАБОТА №2

Вариант 1

ИТОГО: 6 баллов: «5» - 6б; «4» - 4б; «3» - 2б.

Вариант 2

РЕЙТИНГОВЫЙ ЛИСТ

по теме: Фигуры вращения. Цилиндр. Конус.

Ф.И. _______________________________________________, класс ________

ИТОГО: 64 балла

«5» - 58 - 64б;

«4» - 46 - 57 б;

«3» - 32 - 45 б.

Литература:

1. учебная программа по предмету «Геометрия» (10-11 классы, естественно-математическое направление). Астана 2013.

2. Инструктивно-методическое письмо «Об особенностях преподавания основ наук в общеобразовательных организациях Республики Казахстан в 2013-2014 учебном году»

3. Государственный общеобразовательный стандарт среднего образования.

4. Учебник «Геометрия» 11 класс, ЕМН, В.Гусев, Ж.Кайдасов, А.Кагазбаева.Алматы «Мектеп» 2011.

5. Сборник задач. Геометрия 11, ЕМН, В.Гусев, Ж.Кайдасов, А.Кагазбаева.Алматы «Мектеп» 2011.

6. Дидактические материалы. Геометрия 11, ЕМН, В.Гусев, Ж.Кайдасов, А.Кагазбаева.Алматы «Мектеп» 2011.

7. Методическое руководство. Геометрия 11, ЕМН, В.Гусев, Ж.Кайдасов, А.Кагазбаева.Алматы «Мектеп» 2011.