| Контрольная работа № 1. | |
| 1 вариант
1). Выполнить деление многочленов: ( х4 + х3 + х2 – х – 2 ) : ( х3 + х – 2 ) 2). Найти действительные корни уравнения: 2х4 + 3х3 – 10х2 – 5х – 6 = 0 3). Решить уравнение:
4). Решить систему уравнений:
5). Решить задачу: Площадь прямоугольного треугольника равна 15 см2. Найти катеты. | 2 вариант
1). Выполнить деление многочленов: (2 х4 +2 х3 – 5 х2 – 2 ) : ( х3 + х – 2 ) 2). Найти действительные корни уравнения: 3х4 + 3х3 – 8х2 – 2х + 4 = 0 3). Решить уравнение:
4). Решить систему уравнений:
5). Решить задачу: Сумма диагоналей ромба равна 49 см. Площадь этого ромба равна 294 см2. Найти диагонали ромба. |
| Контрольная работа № 2 | |
| 1 вариант
1). Вычислите:
2). Найдите значение выражения:
3). Решите уравнение: а). х4 = 80 ; б). х6 = – 18 ; в). 2х3 – 128 = 0 ; г). х5 + 32= 0 4). Упростите:
5). Найдите значение произведения:
| 2 вариант
1). Вычислите:
2). Найдите значение выражения:
3). Решите уравнение: а). х4 = 20 ; б). х8 = – 36 ; в). 64х3 = 1 ; г). 8 + х3 = 0 . 4). Упростите:
5). Найдите значение произведения:
|
| Контрольная работа № 3 | |
| 1 вариант 1). Постройте график функции а). Найдите область определения функции; б). Какие значения принимает функция ? в). Является ли функция четной или нечетной ? г). Укажите промежутки возрастания ( убывания ) функции; промежутки, в которых функция принимает положительные ( отрицательные значения ).
2). Найдите область определения функции:
3). Не выполняя построения графиков функций у = 6х и 4). Решите иррациональное уравнение:
| 2 вариант 1). Постройте график функции а). Найдите область определения функции; б). Какие значения принимает функция ? в). Является ли функция четной или нечетной ? г). Укажите промежутки возрастания ( убывания ) функции; промежутки, в которых функция принимает положительные ( отрицательные значения ).
2). Найдите область определения функции:
3). Не выполняя построения графиков функций у = 2х и 4). Решите иррациональное уравнение:
|
| Контрольная работа «Арифметическая и геометрическая прогрессии» | |
| 1 вариант
1). Найдите восемнадцатый член арифметической прогресс, если а1 = 7 и d = 4 . 2). Найдите сумму шестнадцати первых членов арифметической прогрессии: - 8; - 4; 0;… 3). Первый член геометрической прогрессии равен 11, а знаменатель прогрессии равен 2. Найдите сумму пяти первых членов этой прогрессии. 4). Является ли число 104 членом арифметической прогрессии, в которой а1 = 5 и а9 = 29 ? 5) Найдите сумму пяти первых членов геометрической прогрессии, если в5 = 81 и в3 = 36. 6). Найдите сумму пятидесяти первых чётных натуральных чисел.
| 2 вариант
1). Найдите двадцатый член арифметической прогресс, если а1 = – 8 и d = 2 . 2). Найдите сумму восемнадцати первых членов арифметической прогрессии: 7; 11; 15;… 3). Первый член геометрической прогрессии равен 4, а знаменатель прогрессии равен 2. Найдите сумму семи первых членов этой прогрессии. 4). Является ли число – 86 членом арифметической прогрессии, в которой а1 = – 1 и а10 = – 46 ? 5) Найдите сумму шести первых членов геометрической прогрессии, если в2 = 4 и в4 = 1. 6). Найдите сумму всех натуральных чисел от 2 до 92 включительно. |
| Контрольная работа № 5 | |
| 1 вариант
1). Найти седьмой член геометрической прогрессии, если в1 = – 25 и q = 2 3). Найдите сумму бесконечно убывающей геометрической прогрессии: 4). 5). Представьте в виде обыкновенной дроби бесконечную периодическую десятичную дробь: а). 0,(31); б). 0,5(6).
| 2 вариант
1). Найти шестой член геометрической прогрессии, если в1 = 4 и q = 2). 3). Найдите сумму бесконечно убывающей геометрической прогрессии: – 16; – 8; – 4; … 4). Найдите сумму шести первых членов геометрической прогрессии, если в2 = 4 и в4 = 1. 5). Представьте в виде обыкновенной дроби бесконечную периодическую десятичную дробь: а). 0,(23); б). 0,1(3).
|
| Итоговая контрольная работа ( 2 часа ) | |
| 1 вариант
1). Упростите выражение:
2). Решите систему уравнений:
3). Найдите область допустимых значений функции:
4). Постройте график функции 5). Найдите сумму пятидесяти первых четных натуральных чисел. 6). Найдите сумму одиннадцати первых членов арифметической прогрессии, если а1 = – 3 , а2 = 8. 7). Бригада должна была изготовить 40 деталей к определенному сроку. Изготовляя в час на 8 деталей больше запланированного, бригада уже за 2 часа до срока перевыполнила план на 8 деталей. Сколько деталей в час должна была изготовлять бригада по плану?.
| 2 вариант
1). Упростите выражение:
2). Решите систему уравнений:
3). Найдите область допустимых значений функции:
4). Постройте график функции 5). Найдите сумму всех нечетных чисел от 1 до 100. 6). Найдите сумму шести первых членов геометрической прогрессии, если в6 = 200 , q = 10. 7). Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 минут вслед за ним выехал второй велосипедист, который прибыл в пункт В на 15 минут раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч меньше скорости второго? |

 Получите свидетельство
Получите свидетельство Вход
Вход



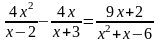
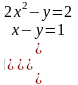

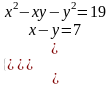
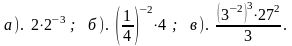
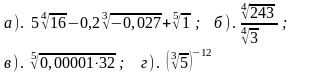
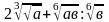
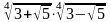
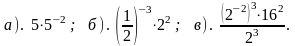
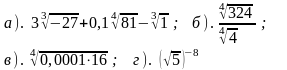
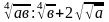
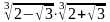
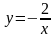
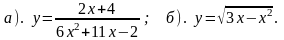
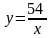 , найдите координаты точек их пересечения.
, найдите координаты точек их пересечения.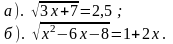
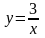
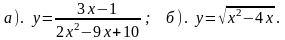
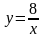 , найдите координаты точек их пересечения.
, найдите координаты точек их пересечения.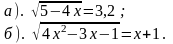
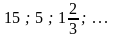
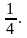
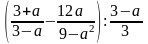
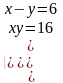









 Контрольные работы по алгебре для 9 класса (67.77 KB)
Контрольные работы по алгебре для 9 класса (67.77 KB)
 0
0 449
449 8
8 Нравится
0
Нравится
0



