Методическая разработка по теме
«Контрольно-методические срезы
по определению уровня обучаемости и обученности учащихся по математике как элементы технологии учета и развития индивидуального стиля учебной деятельности»
Учитель математики: Гималова Т.М., 1 квалификационная категория.
Обучаемость – проявляется как уровень самостоятельности в учебной деятельности ученика.
3 уровень обучаемости – творческий уровень (способность самостоятельно интегрировать новые знания в систему собственных знаний, умение проектировать новые способы решения и т.д.)
2 уровень обучаемости – прикладной уровень (способность активно использовать приобретенные знания в знакомой ситуации)
1 уровень – репродуктивный уровень обучаемости, позволяющий ученику понимать и запоминать новую информацию, применять её по алгоритму.
Меньше 1 – случай, когда ученик не может на уроках данного предмета проявить даже минимальные возможности (группа учебного риска).
Методика определения уровня обучаемости
- Учитель выбирает небольшой по объему новый учебный материал, изложение и представление которого займет не более 7-8 минут (5-7 класс), 8 минут (8-9 класс) и 10-12 минут (10-11 класс).
- Учитель объясняет новый материал, работая по возможности в разных модальностях.
- Учитель проводит этап первичного закрепления новой информации (5-7 минут).
- Учитель организует самостоятельную работу учащихся, в ходе которой учащиеся отвечают на пять вопросов:
1. О чем вы узнали на уроке?
2.Ответьте на вопрос по содержанию нового материала.
3. Выполните задания по образцу
4. Выполните задание в измененной ситуации
5. Примените полученные знания в новой ситуации, найдите связь с жизнью, с другими учебными предметами.
Если правильно выполнены все задания, можно говорить о творческом уровне обучаемости. Если ученик справился с четырьмя заданиями, то это говорит о прикладном уровне обучаемости. Если выполненными оказываются три первых задания – этот ученик демонстрирует репродуктивный уровень обучаемости.
Контрольно-методические срезы (КМС) по определению обучаемости учащихся я провожу в начале учебного года и на основе анализа определяю дозу педагогической помощи в зоне ближайшего развития ученика.
Примеры.
5 класс. Тема урока «Вычитание натуральных чисел»
Вопросы и задания
1. Что вы узнали нового на уроке?
2. Какие свойства вычитания чисел вам известны?
3. Решите пример по образцу:
а) 2 5375+ 1 6686 – 2 1239 б) 6 011 – (1 511 + 432)
4. Упростите выражение (задание в измененной ситуации):
(а + 546) –328
5. Выполните задание в новой ситуации:
18 мин 22 с – 14 мин 39 с
6 класс Тема урока «Деление дробей»
Вопросы и задания
1. Что вы узнали нового на уроке?
2. Какое правило деления дробей надо применять?
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
3. Решите пример по образцу:
Образец
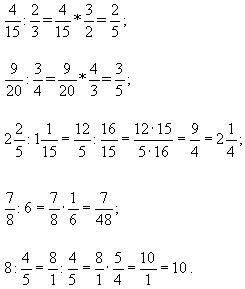
Выполнить самостоятельно:
![]()
4. Упростите выражение (задание в измененной ситуации):
Использование формулы в вычислениях: ![]()
Выполнить самостоятельно:
![]()
5. Выполните задание в новой ситуации:
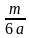 :
: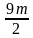 =
=
9 класс. Тема урока «Решение неравенств методом интервалов»
Вопросы и задания
1. Что вы узнали нового на уроке?
2. Как определить знак интервала на числовой оси?
3. Решите неравенство по образцу:
1 вариант: X2 + 4X +3 ≤ 0 ; 2 вариант: X2 + 3X +2 ≤ 0
4. Выполните задание в измененной ситуации
1 вариант: ( -2X +3)( X +1) 0 ; 2 вариант: ( -5X +2)( X +3) 0
5. Выполните задание в новой ситуации:
найти область определения функции
1 вариант: √( X - 2)(X +1)( X -1)2 ; 2 вариант: √()( X +2)2( X - 6)(X +3)
11 класс. Задания для определения уровня обучаемости (входящий контроль, сентябрь 20__ года) 1)Выпишите коэффициенты a, b, c квадратичного неравенства х 2–225+6х0
a) 0 -225 6 b) 1 6 -225 c) 1 -225 6
2)Закончите формулировку теоремы: «Отрезки параллельных прямых, заключённые между параллельными плоскостями,…» А) всегда перпендикулярны этим плоскостям; Б) перпендикулярны друг другу; В) равны между собой; Г) пересекаются. Сделайте чертёж. Запишите кратко (символически), что в теореме дано, и что надо доказать.
3) Исследуйте функцию (по указанному алгоритму) и постройте её график: f(x)=2sin x – sin x.
4)Отрезок АВ перпендикулярен плоскости α (В∈α), АС и АD – наклонные. ∠АСВ =45 0 , АС =8 , ВD =6. Найдите АD.
5) Найдите наибольшее и наименьшее значение функции f (х)=3х 5 – 5х 3 на промежутках [0; 2]и[2; 3]
Тест на обучаемость по теме « Логарифмы» (промежуточный контроль, январь 20__ года)
1) Напишите, что нового вы узнали на уроке .
2) Всегда ли можно найти логарифмы по любому основанию?
3) Выразите log 9 11 через логарифм с основанием 11.
4) Вычислите, не используя МК, lg2 2lg3 lg27 lg12
5) Вычислите log 2 Х +log 8 Х = 8
Если выполнены все задания, можно говорить о третьем (творческий), очень высоком уровне обучаемости.
Если ученик справился с четырьмя заданиями - это второй, (преобразующий) также высокий уровень обучаемости.
Если выполнено три и менее заданий - первый репродуктивный уровень обучаемости.
Итоги КМС по определению обучаемости
1 – репродуктивный уровень обучаемости - ________ чел., ____%
2- прикладной уровень обучаемости - _________ чел., ____%
3 – творческий уровень обучаемости — _________ чел., ____ %
|
| Список учащихся класса | 1 уровень репродуктивный
| 2 уровень прикладной | 3 уровень творческий |
| 1 |
|
|
| + |
| 2 |
| + |
|
|
| 3 |
|
| + |
|
| 4 |
|
| + |
|
По данным определения обучаемости учащихся класса выявляются особенности детей, для которых необходим индивидуальный подход на уроках
| № | Фамилия,имя | Обученность | обучаемость | Визуальная модальность | Аудиальная модальность | Кинестетик | Равнополушарии | Правополушарии | Левополушарии | Мотивация |
| 1 |
| 2 | I | * |
|
| * |
|
| Соц.-дух. |
| 2 |
| 3 | I |
| * |
| * |
|
| Соц. |
| 3 |
| 3 | I | * |
|
| * |
|
| Соц. |
Чтобы получить ожидаемый результат, учитель планирует коррекционную работу со слабоуспевающим учеником. Учителю необходимо в первую очередь знать особенности учащихся, ориентироваться на конкретные причины неуспеваемости, чтобы выбрать стратегию работы с детьми. В обучении математике важным звеном является целенаправленная работа по ликвидации пробелов в знаниях учащихся, которую предваряет объективная содержательная оценка уровня усвоения учащимися изученного материала.
Обученность – объем и глубина знаний ученика по предмету, уровень владения метапредметными умениями и навыками. Обученность определяется после применения технологии ИСУД , оценивается в баллах (отметка по предмету) по качеству и содержанию устных ответов, по результатам контрольных, зачетных работ и т.п..
Приведу пример определения уровня обученности по математике учащихся 9 класса
Тема срезовой контрольной работы: «Квадратичная функция»
Вариант 1.
1. Вычислить значения функции 2Х2 - 4Х+ 1 при Х=5, Х=-2
2.Изобразите схематически график функции:
а) у =- 3х2; б) у = 2х2 – 3.
3.Постройте график функции у = х2 – 5х + 6.
С помощью графика найдите:
а) промежутки знакопостоянства функции;
б) промежутки возрастания и убывания функции;
в) область значения функции.
4. Пересекаются ли прямая у = 2х -1 и парабола у = х2 + 3?
5. Найдите наибольшее значение функции у = -3х2 - 6х + 5.
Вариант 2.
1. Вычислить значения функции 5Х2 + 2Х- 7 при Х=1, Х=-2
2. Изобразите схематически график функции:
а) у = 3х2; б) у = - 2(х + 1)2.
3. Постройте график функции у = х2 – х - 2. С помощью графика найдите:
а) промежутки знакопостоянства функции;
б) промежутки возрастания и убывания функции;
в) область значения функции.
4. пересекаются ли прямая у = 5х -2 и парабола у = х2 + 4?
5. Найдите наибольшее значение функции у = -2х2 + 4х - 7.
| Список учащихся класса | Проверяемые элементы | Оценка (уровень усвоения) | Обученность | |||||||
| Находить значение функции при заданном аргументе | Изображать схематически график функции | строить график квадратичной функции, используя формулу координат вершины параболы | Определять свойства функции ( промежутки знакопостоянства , нули ф., промежутки монотонности | определять пересечение графиков функций | Находить наибольшее значение функции |
|
| |||
|
| + | + | + | + | + | + | 5 | 100% | ||
|
|
| + |
|
|
|
| 2 | 16,7% | ||
|
| + |
|
|
|
|
| 2 | 16,7% | ||
|
| + | + | + |
|
|
| 3 | 50% | ||
Итоги уровня обученности
Если ученик выполнил: 80%-100% заданий - оптимальный уровень – оценка «5»
65-80% - базовый уровень - оценка «4»
50 – 65% - допустимый уровень - оценка « 3»,
ниже 50%– недопустимый уровень – оценка «2»
Обученность класса определяется по формуле
Е/ N*n, где Е – число выполненных заданий срезовой контрольной работы, N – число учащихся класса, п – число заданий контрольной работы.
Используемая литература
Галева Н.Л. Сто приемов для учебного успеха ученика на уроках биологии: Методическое пособие для учителя. – М.: «5 за знания», 2006.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Картотека дифференцированных заданий самостоятельных работ по геометрии с использованием технологии ИСУД (33.46 KB)
Картотека дифференцированных заданий самостоятельных работ по геометрии с использованием технологии ИСУД (33.46 KB)
 0
0 262
262 5
5 Нравится
0
Нравится
0


