Зачёт по геометрии 1 вариант часть А ( 1 балл)
1.Сколько прямых, перпендикулярных к данной плоскости проходит через данную точку пространства. а) одна; б)ни одной; в)две; г)много
2.Угол между прямыми равен 90º, как называются эти прямые
а) параллельные ; б)скрещивающие ; в) перпендикулярные ;
3.Выберите верное утверждение
а) параллелепипед состоит из шести треугольников ;
б)параллелепипед имеет 10 ребёр ;
в) диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам ;
4.Сколько рёбер имеет параллелепипед а)10 ; б) 12 ; в) 24 ; г) 6
5.Апофема пирамиды –это: а) высота пирамиды ; б) высота боковой грани;
6.Сфера является поверхностью : а)конуса ; б) усечённого конуса ; в) цилиндра ; г)шара ;
7. У прямой призмы все боковые грани :
а) параллелограммы ; б) прямоугольники ; в) ромбы ; г) квадраты ;
8. Какое наименьшее число граней может иметь пирамида а) 5 ; б) 12 ; в) 10 ; г) 6 ; д) 4;
9. Сколько диаметров у сферы
а)1 ; б) 2 ; в) 3 ; г) бесконечно много ;
10.Какой фигурой является сечение шара плоскостью
а) отрезком ; б) квадратом ; в) кругом ;
11.Если прямые АВ и СД не лежат в одной плоскости, то они:
а) пересекаются ; б)скрещиваются; в) параллельны.
12.Верно ли, что если все рёбра треугольной пирамиды равны, то она является правильной:
а) да ; б) нет.
Часть В (2 балла)
1. Ребро куба равно 2 см. Вычислите сумму длин всех ребер куба.
А. 24 см; Б. 48 см; В. 12 см; Г. 60 см.
2.Площадь грани куба равна 16 см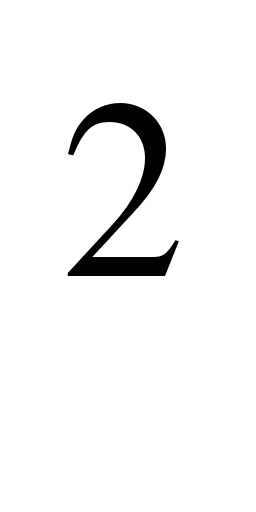 . Вычислите его объем.
. Вычислите его объем.
А. 24 см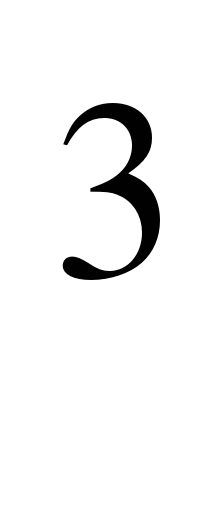 ; Б. 48 см
; Б. 48 см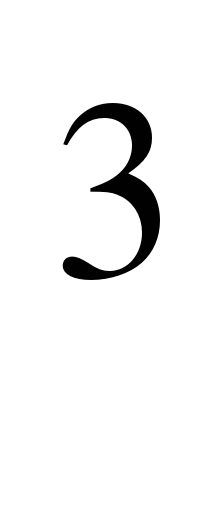 ; В. 56 см
; В. 56 см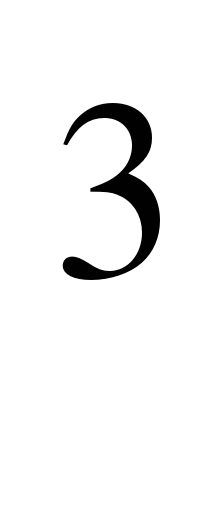 ; Г. 64 см
; Г. 64 см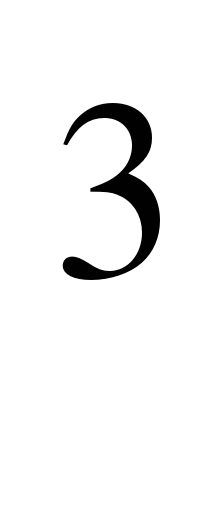 .
.
3. Найдите объём прямоугольного параллелепипеда, если стороны его основания 2см , 3см, а высота равна 5 см . а) 30 ; б) 15 ; в) 20 ; г) 25
4. Вычислите диагональ куба, если ребро куба равно 1. а) 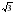 ; б) 1 ; в) 9 ;
; б) 1 ; в) 9 ;
5.Объем пирамиды определяется по формуле, где 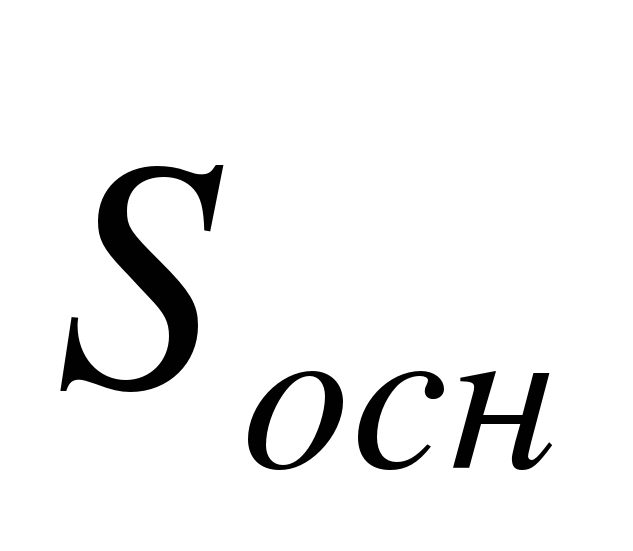 -площадь основания,H- высота, R – радиус.
-площадь основания,H- высота, R – радиус.
А. 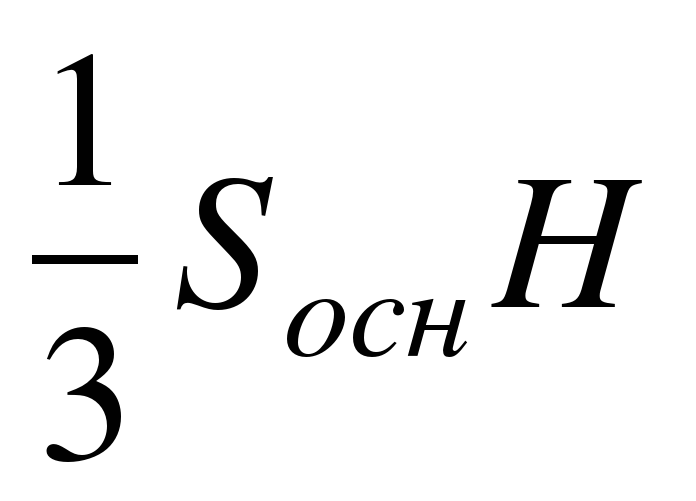 ; Б.
; Б. 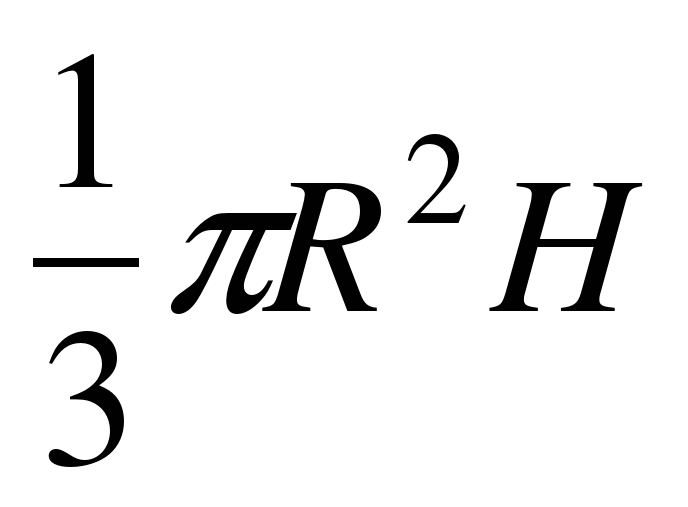 ; В.
; В. 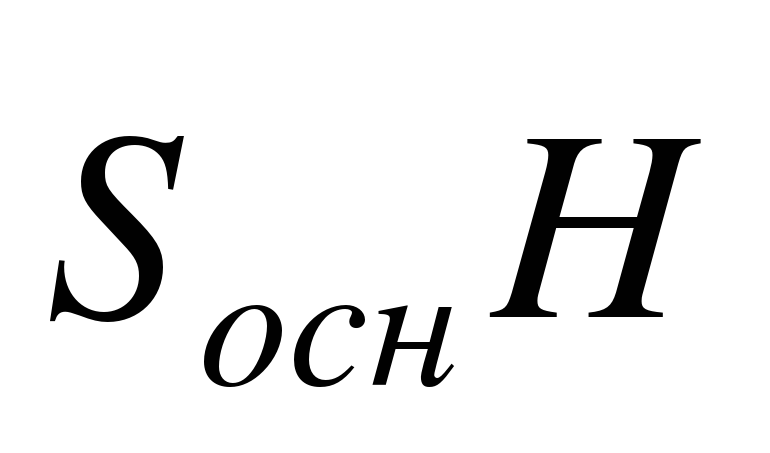 ; Г.
; Г. 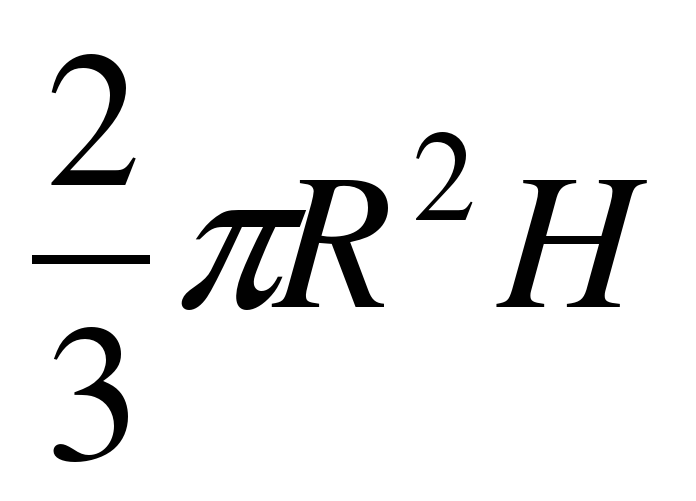 .
.
Часть С ( 3балла)
1.Найдите координаты середины отрезка АВ, если А(5;-4;6) и В( 3;2:-4)
а) ( 4;1;-1 ) ; б)( -4;0;-1 ) ; в) ( 4;-1;1 ) ; г)( 0;-1;1 ) ;
2.Даны векторы 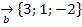
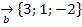 и
и 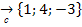
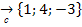 . Найдите
. Найдите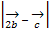
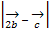 .
.
3.Высота конуса равна 12 м, а образующая 13 м. Найдите площадь осевого сечения конуса.
а) 144 ; б) 120 ; в) 50 ; г) 60 ;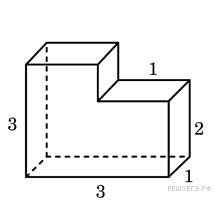
4.Найти объём цилиндра с высотой, равной 3 см и диаметром 6 см
а) 27π ; б) 9π ; в) 36π ; г) 18π ; д) 54π
5. Найдите объем многогранника, изображенного на рисунке
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 30-37 |
| « 4» (хорошо) | 20-29 |
| « 3» (удовлетворительно) | 10- 19 |
| « 2 « (неудовлетворительно) | менее 10 |
Зачёт по геометрии 2 вариант часть А ( 1 балл)
1.Сколько рёбер имеет параллелепипед а)10 ; б) 12 ; в) 24 ; г) 6
2.Что больше: перпендикуляр или наклонная, проведённые из одной точки к плоскости
а) наклонная ; б) равны ; в) перпендикуляр ;
3.Сколько граней у шестиугольной пирамиды а) 6 ; б)7 ; в) 8 ; г) 12 ;
4. Осевым сечение конуса является : а) прямоугольник ; б) треугольник ; в) ромб ; г) квадрат
5. Какой не может быть призма : а) прямой ; б) наклонной ; в) правильной ; г) усечённой ;
6.Сферу пересекает плоскость, сколько точек пересечения может быть
а) одна ; б) две; в) бесконечное множество ; г) ни одной ;
7.Назовите общую прямую плоскостей РВМ и МАВ: а) РМ ; б)АВ ; в) РВ ; г)ВМ ;
8.Назовите элемент не принадлежащий конусу:
а) образующая ; б) ось ; в) высота ; г) медиана ;
9. Прямоугольный параллелепипед- это : а) пирамида ; б) призма ; в) октаэдр ; г) тетраэдр ;
10.Сколько можно провести плоскостей через две пересекающие прямые
а) одну; б)ни одной; в)две; г)много
11.Какой фигурой является сечение шара плоскостью
а) отрезком ; б) квадратом ; в) кругом ;
12.Высота боковой грани правильной пирамиды, проведённая из её вершины, называется
а)диагональю ; б) медианой ; в) апофемой ;
Часть В (2 балла)
1. Какая формула используется для вычисления объема призмы, где R – радиус основания, H – высота: А. 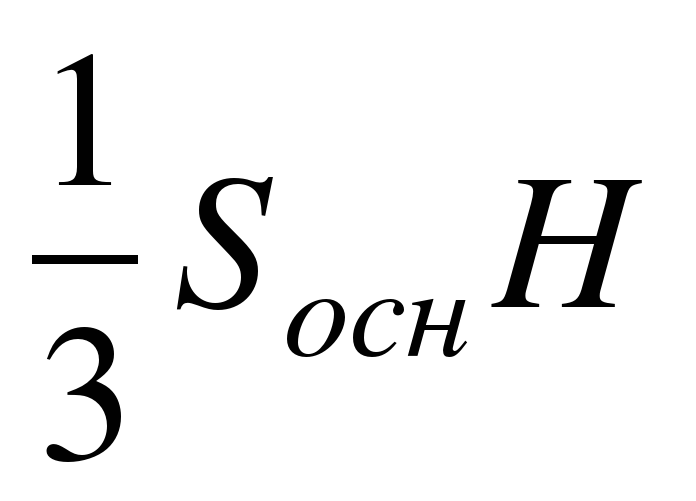 ; Б.
; Б. 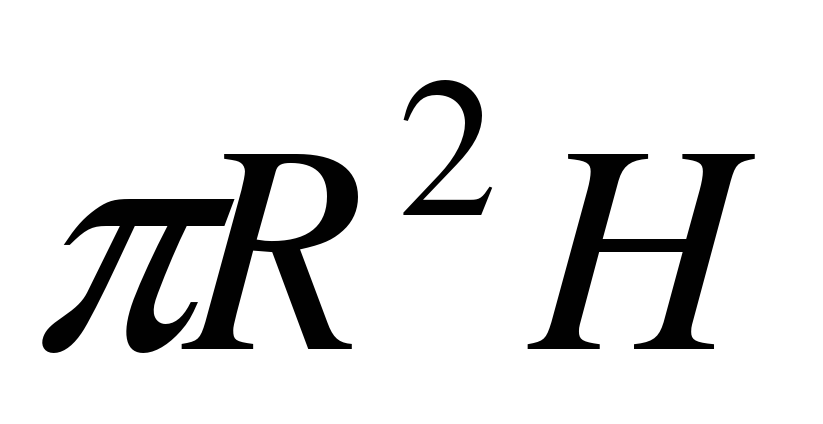 ; В.
; В. 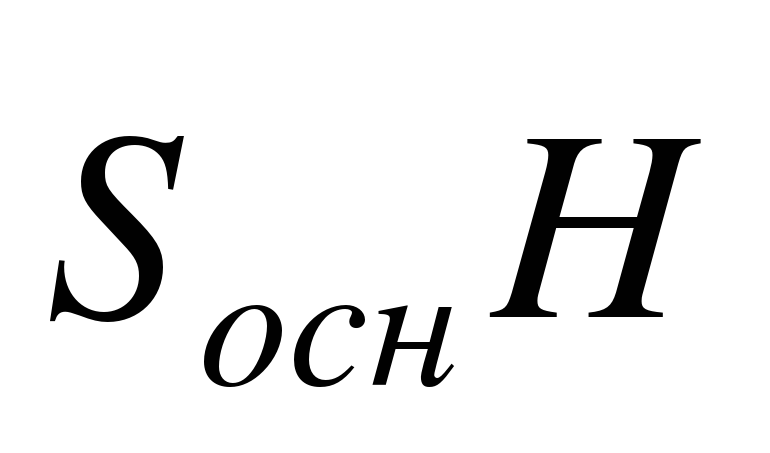 ; Г.
; Г. 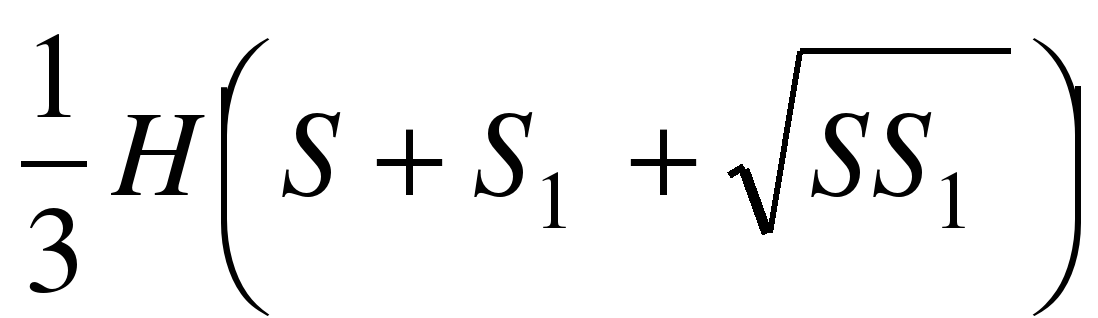 .
.
2. Найдите объём прямоугольного параллелепипеда, если стороны его основания 3см , 4см, а высота равна 7 см .
а) 84 ; б) 28 ; в) 21 ; г) 85
3.Высота конуса 3 см, образующая 5 см. Найдите его объем
а) 27π см3; б) 9π см3; в) 16π см3; г) 18π см3; д) 54π см3.
4. Дан прямоугольный параллелепипед с измерениями 8см,9см и 12 см. Найти диагональ.
а) 289 ; б) 17 ; в) 29 ; г) 5
5. Найдите боковое ребро правильной четырёхугольной, пирамиды, у которой сторона основания 8 м, а высота равна 10 м.
а)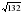 м; б) 132 ; в) 16 ;
м; б) 132 ; в) 16 ;
Часть С( 3 балла)
1.Найдите координаты вектора 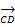
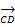 ,если C(6;3;-2) и D(2;4;-5).
,если C(6;3;-2) и D(2;4;-5).
2.Даны векторы 
 и
и 
 Найдите
Найдите
 .
.
3. Объём цилиндра равен 12 см3. Чему равен объём конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
4.Найдите объём куба, если площадь его развёртки равна 96 см2.
5. Найдите объем V части цилиндра, изображенной на рисунке.
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 30-37 |
| « 4» (хорошо) | 20-29 |
| « 3» (удовлетворительно) | 10-19 |
| « 2 « (неудовлетворительно) | менее 10 |
Начало формы
![]() . Вычислите его объем.
. Вычислите его объем. ![]() ; Г. 64 см
; Г. 64 см ![]() .
.
 Получите свидетельство
Получите свидетельство Вход
Вход


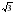 ; б) 1 ; в) 9 ;
; б) 1 ; в) 9 ; 
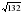 м; б) 132 ; в) 16 ;
м; б) 132 ; в) 16 ;








 Итоговый зачёт по геометрии (0.72 MB)
Итоговый зачёт по геометрии (0.72 MB)
 0
0 1131
1131 140
140 Нравится
0
Нравится
0






