Итоговое повторение по теме «Площади фигур»
Тип урока: урок закрепления знаний, умений и навыков
| Цель деятельности учителя | Создать условия для систематизации по теме «Площади фигур» для подготовки к сдаче ОГЭ | |
| Планируемые результаты | ||
| Предметные умения | Универсальные учебные действия | |
| Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, осуществлять классификации, проводить логические обоснования, доказательства математических рассуждений | Познавательные: систематизировать материал, полученный при изучении темы «Площади» в 8, 9 классах, ориентироваться в учебнике, находить нужную информацию, уметь осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: оценивать результаты деятельности, анализировать собственную работу, планировать свое действие в соответствии с поставленной задачей, определять цель учебной деятельности в сотрудничестве с учителем, контролировать и оценивать процесс и результаты деятельности. Коммуникативные: слушать собеседника, формулировать собственное мнение и позицию, с достаточной полнотой выражать свои мысли. Личностные: способность к самооценке на основе критерия успешности учебной деятельности. | |
| Структура и ход урока | ||
| 1.Организационный момент | ||
| - Сегодня мы с вами проводим урок – практикум по решению задач на тему «Площади фигур». На этом уроке мы с вами повторим формулы площадей, будем решать устные, письменные и практические задачи по этой теме. Для того, чтобы успешно решать задачи, необходимо знать основные понятия и формулы, уметь пользоваться терминами, которые будут использоваться при решении задач. | ||
| 2. Актуализация опорных знаний учащихся | ||
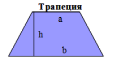
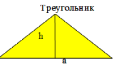
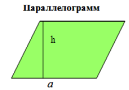
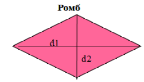
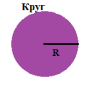
| Соотнесите формулы и чертежи | ||
|
|
| |
| - Вы должны поменяться карточками и проверить работу соседа. Верные формулы отмечаем знаком «+», а неверные знаком «-». Посчитаем количество верных формул. Все формулы верны - ставится оценка «5»; 1 – 2 ошибки – оценка «4»; 3 ошибки – оценка «3»; более 3-х ошибок – оценка «2». |
| |
| 3. Решение задач | ||
| В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 450. Найдите площадь трапеции. Найдите площадь треугольника, две стороны которого равны 4 и 6, а угол между ними 600. Найдите площадь заштрихованной фигуры, если R=6.
| ||
| Проверочная работа | ||
| Вариант 1 1. Если в треугольнике ABC основание АС равно 8 см, а высота, опущенная на АС, равна 7 см, то площадь треугольника равна: а) 56 см2; б) 28 см2; в) 30 см2. 2. Если диагональ квадрата равна 8 см, то его площадь равна: а) 64 см2; б) 256 см2; в) 32 см2. 3. Если основания трапеции равны 15 см и 9 см, а высота 4 см, то площадь трапеции равна: а) 24 см2; б) 48 см2; в) 28 см2. 4. В параллелограмме АВСD стороны равны 4 см и 7 см, а угол между ними составляет 45°, тогда его площадь равна: а) 7 5. Площадь круга, вписанного в квадрат со стороной 12 см, равна: а) 36 см2; б) 12 см2; в) 72 см2. Вариант 2. 1. Если в треугольнике ABC основание АС равно 6 см, а высота, опущенная на АС, равна 9 см, то площадь треугольника равна: а) 54 см2; б) 27 см2; в) 30 см2. 2. Площадь круга, описанного около правильного шестиугольника со стороной 6 см, равна: а) 12 см2; б) 36 см2; в) 72 см2. 3. В прямоугольнике одна из сторон равна 6 см, а диагональ – 10 см, тогда его площадь равна: а) 24 см2; б) 60 см2; в) 48 см2. 4. Если диагонали ромба равны 10 см и 12 см, то его площадь равна: а) 240 см2; б) 60 см2; в) 120 см2. 5. Если в равностороннем треугольнике АВС сторона АВ = 12 см, то его площадь равна: а) 36 По одному ученику из каждого варианта выходят к доске и записывают свои ответы. Учитель проверяет и оценивает их, остальные учащиеся самостоятельно проверяют свои ответы. | ||
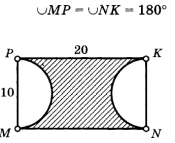
| Решение задач по готовым чертежам. | ||
|
| ||
| Итоги урока. | ||
| - Перечислите основные проблемы и трудности, которые вы испытывали во время урока. Какими способами вы их преодолели? | ||
| Домашнее задание. | ||

 Получите свидетельство
Получите свидетельство Вход
Вход





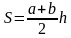
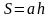
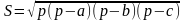
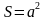
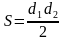
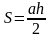
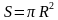
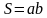
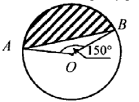
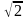 см2 ; б) 14
см2 ; б) 14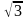 см2; б) 72
см2; б) 72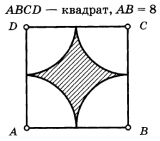









 Итоговое повторение по теме "Площади фигур" (254.9 KB)
Итоговое повторение по теме "Площади фигур" (254.9 KB)
 0
0 324
324 37
37 Нравится
0
Нравится
0


