Исследовательская работа "Рациональные уравнения"

Муниципальное бюджетное общеобразовательное учреждение

«Горельская СОШ» в с. Малиновка

Конкурс исследовательских и творческих работ обучающихся

«ПЕРВЫЕ ШАГИ В НАУКУ»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

Рациональные уравнения

Математика

Выполнила:

ученица 9 «ж» класса филиала «Горельская СОШ в селе Малиновка

Коробанова Татьяна

Руководитель:

Четырин Зоя Владимировна

учитель математики.

2019 год.

Содержание

Введение. 2-4

1. Основная часть

1.1.Теоретические сведения 5

1.2.Из истории рациональных чисел 5-9

1.3. Методы решения рациональных уравнений 9-10

1.4.Классификация рациональных уравнений 11-12

2.Практическая часть

2.1. Решение рациональных уравнений с использованием

основных методов 13-15

2.2. Решение рацональных уравнений с использованием 1

особых методов и приёмов 15-20

3. Результаты исследования 21

Заключение 22

Литература 23

Ученый С. Коваль писал «Уравнения – это золотой ключ, открывающий все математические сезамы»

Поэтому выбор темы моего исследования не случаен, так как решение уравнений - самый распространенный тип экзаменационных задач. Проблема заключается в том, что на протяжении всех лет обучения мы решаем уравнения, но школьный курс алгебры предусматривает ограниченный набор решений по данной теме.

Компенсировать недостаток знаний удалось за счёт изучения дополнительной научной литературы и знакомства с новыми типами рациональных уравнений, а также приёмами для их решения. Приобретенные полученные навыки позволят применить их при решении конкурсных задач, подготовиться к ОГЭ, что является актуальным при изучении математики и смежных дисциплин.

Поэтому, поставлена цель работы: выявление способов решения уравнений, отличных от изучаемых в школьной программе.

Для достижения поставленной цели, в работе определены основные задачи:

1. изучить и проанализировать специальную литературу по проблеме исследования;

2. найти информацию о способах решения рациональных уравнений;

3. изучить историю развития уравнений;

4. рассмотреть нестандартные случаи решения рациональных уравнений и применить их на практике;

5. создать банк заданий по теме исследования;

6. Создать буклет для одноклассников.

Объект исследования: рациональные уравнения.

Предмет исследования: изучение нестандартных методов решения рациональных уравнений.

Характер исследования обуславливает необходимость применения комплекса следующих общенаучных методов исследования:

• поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;

• практический « Рациональные уравнения;

• сравнение, анализ, полученный в ходе исследования.

Гипотеза: если знать нестандартные методы решения рациональных уравнений, то это позволит повысить качество выполнения некоторых олимпиадных и тестовых заданий ОГЭ.

Практическая значимость исследования.

Материал данного исследования имеет практическую значимость и будет полезен любознательным школьникам, а так же выпускникам школы. Она позволит улучшить подготовку и расширить математический кругозор в решении уравнений.

Поэтому темой моего исследования выбраны рациональные уравнения.

1.СОДЕРЖАНИЕ

1.1.Теоретические сведения.

Уравнение f(x) = g(x) называется рациональным, если f(x) и g(x) – рациональные выражения [4, с.223].

Решить уравнение – значит найти все его корни или доказать, что корней нет.

Целым уравнением с одной переменной называется уравнение, левые и правые части которого – целые выражения [3, с.72]. Целое рациональное уравнение может быть записано в ви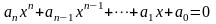де , где 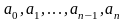– некоторые числа. К простейшим целым рациональным уравнениям относятся линейные и квадратные уравнения.

Дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причем хотя бы одно из них – дробным выражением [3, с.78]. Для решения такого уравнения нужно:

• найти общий знаменатель дробей, входящих в уравнение;

• умножить обе части уравнения на этот знаменатель;

• решить получившееся целое уравнение;

• исключить из его корней те, которые обращают в нуль общий знаменатель дробей [3, с.78].

1.2.История возникновения рациональных уравнений.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Уравнения первой степени с одним неизвестным решали уже в Древнем Египте и в Древнем Вавилоне. Вавилонские писцы умели решать и уравнения второй степени. Евклид решал уравнения второй степени геометрически. Для математиков, уже умевших решать уравнения первой и второй степени, самым желанным было научиться решать уравнения третьей степени. Одним из первых этим вопросом заинтересовался таджикский ученый Омар Хоийен (1048-1122). Омар Хоийен придумал очень сложные и красивые способы геометрических построений для отыскания неизвестного. Но для практического использования они были неудобны.

Многим, разумеется, приходила в голову заманчивая мысль найти и для любой другой степени n2 формулы, которые выражали бы корни уравнения через его коэффициенты с помощью четырех арифметических действий – сложения, вычитания, умножения, деления – и извлечения корней или радикалов, то есть, говоря более кратко, решали бы уравнение в радикалах.

Томас Торквемада–глава инквизиции в Испании, монах-доминиканец – считал, что решение таких уравнений волей бога изъято из возможностей человеческого разума. И когда один из его друзей, математик по имени Паоло Вальмес, неосторожно сказал Торквемаде, что он, Вальмес, умеет решать уравнения даже четвертой степени, Торквемада бросил его в тюрьму, а затем отправил на костер за «борьбу с божественной волей». Вальмес никому не успел сообщить о своем открытии. Это было в конце 15 века.

Для математиков того времени существовало не одно уравнение третьей степени

х³+рх²+qx+r=0,

а несколько, из которых главнейшими были три:

х³+рх=q

х³=рх+q

х³+рх²=q

А почему же не одно? Потому что в те времена рассматривались лишь уравнения с положительными коэффициентами. Первыми из них было решено уравнение х³+рх=q. Это удалось сделать итальянскому математику Сципиону Даль Ферро (1465-1526). Даль Ферро не опубликовал найденного им способа, но некоторые из его учеников знали об этом открытии, и вскоре один из них, Антонио Фиор, решил им воспользоваться.

В это время в итальянском городе Верна жил небогатый учитель математики Никколо Тарталья (1499-1557). Тарталья был очень талантливым человеком и сумел в 1535 году заново открыть прием, изобретенный Сципионом Даль Ферро.

Состоялся поединок между Фиором и Тартальей. По условию, соперники обменялись тридцатью задачами, на решение которых отводилось шестьдесят дней. Но так как Фиор знал по существу только одну задачу и был уверен, что какой-то учитель решить ее не сможет, то все его тридцать задач оказались однотипными. Тарталья был хорошо подготовлен к их решению и справился со всеми тридцатью задачами за два часа. Фиор же не смог решить ни одной из задач, предложенных его противником. Победа прославила Никколо Тарталью на всю Италию, но вопрос о решении уравнений третьей степени еще не был решен до конца, кроме того, надо было привести в систему все, что было известно о решении разных видов кубических уравнений.

Это удалось сделать итальянскому математику Джироламо Кардано (24.9.1501 – 21.9.1576). Он вывел формулу для решения любого кубического уравнения. Кардано родился в Павии. Учился в университетах Павии и Падуи. В молодости занимался медициной. В 1534 году стал профессором математики в Милане и Болонье. Эту формулу Кардано позаимствовал у Никколо Тартальи. Она (формула Кардано) была опубликована в книге Кардано «Великое искусство, или О правилах алгебры» в 1545году.

После открытия в середине 16 века решения в радикалах уравнений третьей и четвертой степени математики смогли констатировать, что уравнения первой – четвертой степени имеют соответственно 1, 2, 3, 4 корня, которые могут быть положительными, равными нулю, отрицательными или мнимыми. Этот факт наводил на мысль о том, что уравнение n-й степени (n0) должно иметь n корней. Впервые эту мысль явно высказал в 1629 году замечательный математик Альберт Жирар в главном своем труде «Новое открытие в алгебре». Жирар, став учеником Симона Стевина, внес значительный вклад в развитие алгебры. Не установлено, была ли книга Жирара известна Декарту.

Этим занимались не только Жирар, Декарт и другие ученые 17 века, но и величайшие математики 18 века и первой половины 19 века, в том числе Эйлер, Даламбер, Лагранж, Лаплас, Гаусс.

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений.

1.3.Методы решения рациональных уравнений.

При изучении математической литературы по данной теме множество рациональных уравнений можно разделить по методу решения.

1. Простейшие

Для решения некоторых рациональных уравнений не требуется знание особых приёмов. Решаются путем простейших упрощений – приведение к общему знаменателю, приведению подобных членов и т.д.

Квадратные уравнения решают по готовым формулам: D = b ² – 4ас,

,

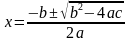а так же формулы Виета

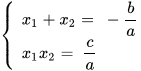
Если это дрбно-рациональные, то находим еще ОДЗ [5, c.6].

1. Группировка

Путем группировки слагаемых, применяя формулы сокращенного умножения привести уравнение к виду, когда слева записано произведение нескольких множителей, справа – ноль. Затем приравниваем к нулю каждый множитель.

3.Подстановка

Ищем в уравнении некоторое повторяющееся выражение, которое обозначаем новой переменной, тем самым упращая вид уравнения.

4.Подбор

При решении уравнений высших степеней рациональные корни уравнения a_nxⁿ + a_{n – 1}x^{n – 1} + …+ a₁x + a₀ = 0 ищем в виде p / q, где p — делитель a₀, q — делитель a_n, p и q взаимно простые числа [5, c.9]

5«Искусство»

Трудность решения в какой-то мере

входит в само понятие задачи:

там, где нет трудности, нет и задачи. (Д. Пойа)

Т.е. решать задачи нестандартно, придумать «свой метод», догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и

умножить и т.д.

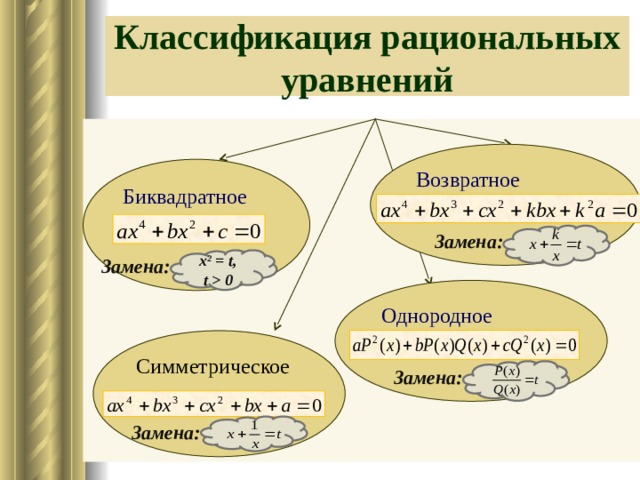
1.4.Классификация рациональных уравнений.

Рациональные уравнения делятся на несколько видов.

1.Биквадратное уравнение.

Уравнения вида ax⁴ + bx² + c = 0, где а не =0, являющееся квадратным относительно х² , называют биквадратными уравнениями [3, 75].

Для его решения используем замену x² = t, где t 0. После подстановки новой переменной получаем уравнение at² + bt + c = 0, решая которое приходим к уравнению x² = t, где t – корни квадратного уравнения [3, с.75].

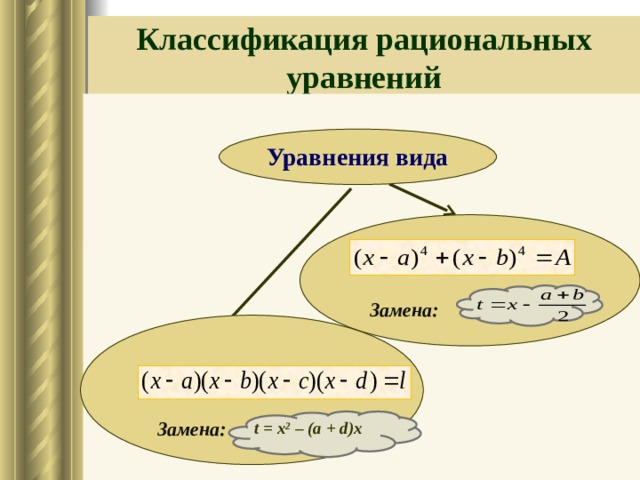
2. Уравнения вида (х+а)⁴ +(х+в)⁴=с сводится к биквадратному, если

сделать подстановку: х= t – (а + b)/2 [5 .с.7].

3. Уравнения вида (х + а)(х + в)(х + с)(х + d)= l сводится к квадратному, если а + в =с + d [ .с.7].

4. Симметрическое уравнение

Уравнения a₀xⁿ + a₁x^{n – 1} + … + a₁x + a₀ = 0 называют симметрическим (коэффициенты членов, равностоящие от концов, равны) решаются с помощью подстановки 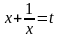, если n – четное, если n – нечетное, то уравнение имеет корень х = -1 [ 5.с.8].

5. Однородные уравнения.

Уравнения вида, ау^2а +bу^а z^а +сz^2а =0, где а, b, c – заданные числа отличные от нуля. Делим оби части уравнения на у^2а не = 0. Получаем а(у/z)^2а +b(у/z)^а + с = 0. Обозначаем (у/z)^а =t, получаем квадратное уравнение относительно t [5 ,с.8].

6.Возвратное уравнение четвёртого порядка: ах⁴ + bх³ +сх² + кbх + к²а = 0 (все коэффициенты отличны от нуля). После почленного деления на х² получаем:

ах² + bх + с + bk/х + а b(k/х)² = 0

а(х² +( k/х)²) + b (х + k/х) + с = 0.

Пусть х+k/х =у, тогда х² +( k/х)² = у² – 2к, а уравнение примет вид:

ау² + bу + с – 2ак = 0 [5 .с.9].

2.ПРАКТИЧЕСКАЯ ЧАСТЬ

Самое трудное при решении рациональных уравнений – правильно определить, к какому виду оно относится. Если идентификация состоялась, тогда метод решения становится очевиден, если же классифицировать уравнение затруднительно, то необходимо придумать, как свести уравнение к более простому.
Рассмотрим примеры с использованием основных методов и неосновных.

2.1.Решение рациональных уравнений с использованием основных методов

Простейшие.

Пример 1. Решить уравнение.

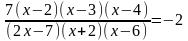[6, с.96].

Решение: 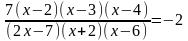; О.Д.З. 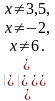(1)

Приводим уравнение к виду 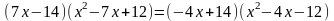, затем раскрываем скобки.

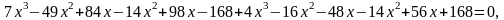
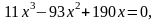
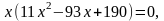
х= 0 или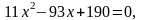

D = 93² – 4·11·190 = 289.

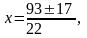
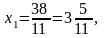
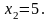
Найденные значения переменной х удовлетворяют соотношениям (1).

Ответ: 0; 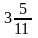; 5.

Группировка.

Пример 2. Решить уравнение. x³ + 2x² - 5x - 6 = 0. [5, c.6]

Решение: x³ + 2x² - 5x - 6 = 0. Стр.6

Представим -6 = 1 - 7 = 1 - 5 - 2 и сгруппируем слагаемые, получим:

(x³ + 1) + (2x² - 2) - (5x + 5) = 0.

Разлагаем первую скобку как сумму кубов и выделим общие множители:

(x + 1) (x² - x + 1) + 2 (x² - 1) - 5 (x + 1) = 0.

Используем формулу разности квадратов:

(x + 1) (x² - x + 1) + 2(x - 1) (x + 1) - 5 (x + 1) = 0,

(x + 1) (x² + x - 6) = 0,

x = -1;

x² + x - 6 = 0.

По теореме Виета получим два корня:

х = -3 и х = 2.

Ответ: х = -3;-1; 2.

Подстановка

Пример 3. Решить уравнение. (x² + x – 5) / x + 3х / (x² + x – 5) + 4 = 0[5, C.7],

Решение: (x² + x – 5) / x + 3 / (x² + x – 5) + 4 = 0,

легко решается с помощью подстановки (x² + x – 5) / x = t, получаем t + (3 / t) + 4 = 0.

t₁ = -3, t₂ = -1.

x² + x – 5) / x = -3, или x² + x – 5) / x = -1

х₁ = -5, х₂ = 1 х₁ = -1 - 6, х₂=-1 + 6

Ответ: -5; 1; -1 - 6; -1 + 6

В рассмотренном примере метод введения новой переменной был, как любят выражаться математики, адекватен ситуации. Но так бывает не всегда.

2.2.Решение нестандартных уравнений с использованием особых методов или приёмов.

Подстановка

Пример 3. Решить уравнение.

(x + 3) ⁴ + (x + 5) ⁴ = 16. [5,c.7]

Решение: (x + 3) ⁴ + (x + 5) ⁴ = 16. Сделаем подстановку х= t - 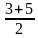,т.е. х=t-4. Тогда получаем

(t-1) ⁴ +(t+1) ⁴=16 ^.

Воспользуемся формулами (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a - b)⁴ = a⁴ - 4a³b + 6a²b² - 4ab³ + b⁴

Получим:

t⁴ -4t³ + 6t² – 4t + 1 + t⁴ + 4t³ + 6t² + 4t + 1=16.

2t⁴ + 12t² – 14=0, t⁴ + 6t² – 7=0.

Положим t⁴ = z  0 гда z² +6z – 7=0, z₁=-7 - посторонний корень, z ₂=1, т.е. t²= 1, t₁=-1, t₂=1. Следовательно, х₁ =-1 – 4=-5, х₂ =1 – 4=-3.

Ответ: -5; -3.

Уравнения вида (х + а)(х + в)(х + с)(х + d)= l сводится к квадратному, если а + в =с + d.

Пример 4. Решить уравнение. (x – 4)(x – 5)(x – 6)(x – 7) = 1680 [5,c.8].

Решение. (x – 4)(x – 5)(x – 6)(x – 7) = 1680.

Перепишим уравнение в виде (x – 4)(x – 7)(x – 5)(x – 6) = 1680, т.е.

(x² – 11x + 28)(x² – 11x + 30) = 1680.

Обозначим x² – 11x + 28 = t, тогда

t(t + 2) = 1680, t² + 2t – 1680 = 0,

t₁ = – 42; t₂ = 40.

Поэтому

x² – 11x + 28 = – 42;

x² – 11x + 70 = 0;

D = 121 – 280  x_1,2.

x² – 11x + 28 = 40;

x² – 11x – 12 = 0;

x₁ = 12; x₂ = – 1.

Ответ: x₁ = 12; x₂ = – 1.

Симметрическое уравнение

Пример 5. 2x⁴ + 3x³ – 16x² + 3x + 2 = 0. [5,с. 8].

Решение: 2x⁴ + 3x³ – 16x² + 3x + 2 = 0. Это симметрическое уравнение четвертой степени. Решаем его почленным деление на x²  0, получим:

2x² + 3x – 16 +3 / x + 2 / x² = 0, т.е.

2(x² + 1 / x²) + 3(x + 1 / x) – 16 = 0,

обозначим x + 1 / x = t, тогда x² + 2 + 1 / x² = t², т.е. x² + 1 / x² = t² – 2, получаем

2(t² – 2) + 3t – 16=0

2t² + 3t – 20 = 0,

t₁ = – 4; t₂ = 5 / 2.

Следовательно, имеем

x + 1 / x = – 4;

x² + 4x + 1 = 0;

x_1,2 = –2 3,

x + 1 / x = 2,5;

2x² – 5x + 2 = 0;

x₃ = 2;

x₄ = 1 / 2.

Ответ: x_1,2 = –2 3; x₃ = 2; x₄ = 1 / 2.

«Однородное уравнение»

Пример 6. 3(х² – х + 1)² – 5(х + 1)(х² – х + 1) - 2(х + 1)² = 0 [5,c.8].

Решение: 3(х² – х + 1)² – 5(х + 1)(х² – х + 1) - 2(х + 1)² = 0.

Разделим обе части данного уравнения на (х + 1)² не=0.

3((х² – х + 1)/ (х + 1))² - 5(х² – х + 1)/ (х + 1) – 2 = 0.
Пусть (х² – х + 1)/ (х + 1) = t, тогда

3t – 5t – 2= 0, или t₁₌2, t₂ = -1/3

Следовательно,

(х² – х + 1)/ (х + 1) =2 или (х² – х + 1)/ (х + 1) = -1/3

х_1,2= 313/2, x.

Ответ: х_1,2= 313/2.

Подбор

Пример 7. Решить уравнение. x³ – x² – 8x + 6 = 0 [5,c.9].

Решение. x³ – x² – 8x + 6 = 0.

Здесь a_n = 1, a₀ = 6. Поэтому, если данное уравнение имеет рациональные корни, то их следует искать среди делителей числа 6: 1, 2, 3, 6. Проверкой убеждаемся, что x = 3, т.к. 27 – 9 – 24 + 6 = 0.

Делим (x³ – x² – 8x + 6) на (x – 3)

Получаем: x³ – x² – 8x + 6 = (x – 3)(x² + 2x – 2), т.е. данное уравнение можно представить в виде:

(x – 3)(x² + 2x – 2) = 0

x – 3 = 0, или x² + 2x – 2 = 0.

x₁ = 3 , x_2,3 = – 1 3

Ответ: x₁ = 3; x_2,3 = – 1 3.

Не всякое уравнение в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать другие методы решения – это «Искусство».

1.Приём выделения квадрата двучлена.

При решении некоторых рациональных уравнений хороший эффект даёт формула «Квадрат двучлена». В результате её выделения «вырисовывается» нужная замена переменных, позволяющая свести уравнение к квадратному.

Пример 8. Решить уравнение. х² + 81х²/(9 + х)² = 40[5,c.13]

Решение: х² + 81х²/(9 + х)² = 40, О.Д.З.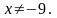

Воспользуемся формулой а² + b² = (а – b)² + 2аb, получаем

(х – 9х/(9 +х))² + 2х· 9х/(9 + х) = 40,

пусть х²/(9 + х)= t.

Тогда t² + 18t – 40 = 0, t₁ = -20, t₂ = 2.

Получаем два уравнения

х²/(9 + х)= 2 или х²/(9 + х)= -20

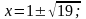
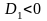, действительных корней нет.

Ответ: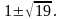

2. Приём почленного деления.

Упростить уравнение нередко помогает почленное деление на выражение с переменной. В этом случае необходимо убедится, что значение переменной, при котором выражение обращается в ноль, не является корнем исходного уравнения.

Такой приём используется в отдельных видах рациональных уравнений. Например, симметрического уравнения четвёртой степени приходится выполнять почленное деление на выражение х². Но не всегда данное уравнение можно соотнести с конкретным видом. Математическая интуиция и наблюдательность «подскажет», на какое выражение надо делить.

Пример 9. Решить уравнение. 13x / (2x² + x +3) + 2x / (2x² – 5x + 3) = 6 [5,c.12].

Решение: 13x / (2x² + x +3) + 2x / (2x² – 5x + 3) = 6.

Разделим числитель и знаменатель дробей на x 0:

13 / (2x + 1 + 3 / x) + 2 / (2x – 5 +3 / x) = 6, обозначим 2x + 3 /x = t.

Получаем

13 / (t + 1) + 2 / (t – 5) = 6,

13t – 65 + 2t + 2 = 6t² – 24t – 30,

6t² – 39t + 33 = 0,

2t² – 13t + 11 = 0,

t₁ = 1; t₂ = 5,5.

Следовательно:

2x + 3 / x = 1; 2x² – x + 3 = 0; D = 1 – 24  x.

2x + 3 / x = 5,5; 4x² – 11x + 6 = 0; x₁ = 2; x₂ = 0,75.

Ответ: x₁ = 2; x₂ = 0,75.

3.Прибавить и отнять в уравнении.

Пример 10. Решить уравнение. х⁴ – 2х³ + х - 3/4 = 0 [5,c.13].

Решение: х⁴ – 2х³ + х - 3/4 = 0.

Прибавим и вычтем в левой части х², выделим полный квадрат, получим.

х⁴ – 2х³ + х² – х² + х – 3/4 = 0, (х² – х)² – (х² – х) – 3/4 = 0.

Пусть х² – х = t, тогда t² – t –3/4=0, t₁ = -0,5, t₂ = 3/2.

Возвращаясь к старой переменной, получаем

х² – х = -0,5, или х² – х = 3/2

x. x_1,2 = (1 7) / 2.

Ответ: (1 7) / 2

3. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

В процессе написания работы изучены и обобщены научные сведения по теме «Рациональные уравнения»:

• сформулировано основное понятие симметрического уравнения, однородного и возвратного;

• рассмотрены основные способы решения рациональных уравнений;

• выявлены приёмы, позволяющие понизить степень уравнения и тем самым упростить процесс решения;

• практически рассмотрены нестандартные случаи решения рациональных уравнений;

• скомплектован банк задач на различные методы рациональных уравнений, представленных в приложении;

• создан буклет «Рациональные уравнения» для учащихся.

В ходе проведённого исследования намечены перспективы: необходимо более детальное изучение приёмов и методов решения отдельных видов рациональных уравнений (рациональные уравнения с модулем).

В связи с этим планируется продолжить научные изыскания в данной области с целью нахождения наиболее рациональных способов решения таких уравнений.

3.1. Заключение

При работе над данной темой было изучено большое количество математической литературы, освоение которой, позволило повысить уровень знаний по математике. Приобретенные навыки при решении рациональных уравнений могут быть использованы при решении неравеств, систем неравенств и уравнений, решении задач, а так же при изучении математики в старших классах и сдачи экзаменов.

В ходе выполнения своей работы я считаю, что с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме. Я пришла к выводу, что все методы надо иметь в своем арсенале и применять их по мере необходимости. Я составила буклет-памятку, в него вошли те виды решения рациональных уравнений, которые не изучаются в школе. Данные буклеты я раздам одноклассникам и ученикам других классов.

Самостоятельный поиск нетрадиционного способа решения уравнения, ведет к быстрому и рациональному способу решения, способствует развитию творческого мышления. Надеюсь, что работа будет полезна всем тем, кто увлекается математикой, кто желает знать свыше программного материала, углубить свои знания.

Хочу закончить словами: « Скажи мне, и я забуду. Покажи мне, и я запомню. Дай мне действовать самому, и я научусь» (китайская пословица).

Литература

1. Г. И. Глейзер. «История математики в школе»

2. Карп А.П. Сборник задач по алгебре и началам анализа: Учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 1995. – 176 с.

3.Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 9 класс – 15-е изд., дороб. – М.: Просвещение, 20

4. Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений / А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2013. – 215 с. : ил.

5. Петрушина С.Н., Жуковский Е.С. Математика для поступающих в вузы: Изд-во ТГУ им. Г.Р. Державина, 2004. 97с.

6. Письменный Д.Т. Готовимся к экзамену по математике. – Москва, Издательство «Айрис», 2005. – 136 с. : ил.

Интернет-ресурс:

7. http://900igr.net/up/datai/83838/0003-003-.jpg

8. https://ds03.infourok.ru/uploads/ex/0de4/0004401b-e1bcc051/640/img10.jpg

9. http://mmetodika.narod.ru/page/urav2.htm

ПРИЛОЖЕНИЕ 1.

Банк заданий по теме «Рациональные уравнения»

1. Подстановка [5,с.9] .

1. 6 - 21/(х² – 4х + 10) = 4х² – х, Ответ: {1;3}

2. 2х⁴ + х³ – 11х² + х + 2 = 0, Ответ: {0,5; 2; (-35)/2}

3. (х + 3/2)⁴ + (х – 1/2)⁴ = 82, Ответ: {1,5; - 2,5}

4. х⁴ – 6х² + 8 = 0, Ответ: {2, 2}.

2.Подбор [5,с.10]

1.х³ – 3х + 2 = 0, Ответ: {1;- 2}

2.х⁴ – х³ – 35х² + 57х + 90 = 0, Ответ: {-1;- 6;3;5}

3.2х + х – 9 =0, Ответ: {3/2}

4.4х⁴ + 8х³ – 3х² -7х + 3 = 0, Ответ: {- 1,5;0,5; (-15)/2}.

3. «Искусство» [5,с.13]

1.6х/(х² + 2х + 3) – 2 + 11х/(х² + 7х + 3) = 0, Ответ: {3;1; (-933)/4}

2. 1/х² + 1/(х + 2)² =10/9, Ответ: {1;3}

ПРИЛОЖЕНИЕ 2.

26

Уравнения вида (х+а) 4 +(х+в) 4 =с, сводится к квадратному, подстановка: х= t – (а+ b )/2

Пример . (x + 3) 4 + (x + 5) 4 = 16.

Решение: (x + 3) 4 + (x + 5) 4 =16.

Сделаем подстановку: х= t – (3+5)/2 , т.е. х= t - 4.

Тогда получаем ( t -1) 4 +( t +1) 4 =16 .

Воспользуемся формулами

(a  b) 4 = a 4  4a 3 b + 6a 2 b 2 4  ab 3 + b 4

Получим :

t 4 -4t 3 + 6t 2 – 4t + 1 + t 4 + 4t 3 + 6t 2 + 4t + 1=16.

2t 4 + 12t 2 – 14=0, t 4 + 6t 2 – 7=0.

Положим t 2 = z  0, где z 2 +6 z – 7=0, z 1=-7 пост.кор. , z 2 =1, t 2 = 1, t 1 = -1, t 2 =1. Следовательно,

х 1 = -1 – 4=-5, х 2 =1 – 4=-3.

Ответ: -5; -3.

Уравнение вида:

(х + а)(х + в)(х + с)(х + d ) = l

сводится к квадратному, если а + в = с + d .

Пример 2. ( x – 4)( x – 5)( x – 6)( x – 7) = 1680.

Решение: ( x – 4)( x – 5)( x – 6)( x – 7) = 1680

Перепишем уравнение

( x – 4)( x – 7)  ( x – 5)( x – 6) = 1680,

( x 2 – 11 x + 28)( x 2 – 11 x + 30) = 1680.

Обозначим x 2 – 11 x + 28 = t , тогда

t ( t + 2) = 1680, t 2 + 2 t – 1680 = 0, t 1 = – 42; t 2 = 40.

x 2 – 11 x + 28 = – 42; x 2 – 11 x + 70 = 0; D = 121 – 280

x 2 – 11 x + 28 = 40; x 2 – 11 x – 12 = 0; x 1 = 12; x 2 = – 1.

Ответ: x 1 = 12; x 2 = – 1.

«Однородное уравнение»

Уравнения вида, ау 2а + b у а z а +с z 2а =0, где а, b , c

заданные числа  0. Делим оби части уравнения

на у 2а  0.Обозначаем (у/ z ) а = t , получаем

квадратное.

Пример . 3(х 2 – х + 1) 2 – 5(х + 1)(х 2 – х + 1) - 2(х + 1) 2 = 0.

Решение: 3(х 2 – х + 1) 2 – 5(х + 1)(х 2 – х + 1) - 2(х + 1) 2 = 0.

Разделим обе части данного уравнения на (х + 1) 2  0.

3((х 2 – х + 1)/ (х + 1)) 2 - 5(х 2 – х + 1)/ (х + 1) – 2 = 0.

Пусть (х 2 – х + 1)/ (х + 1) = t , тогда

3 t 2 – 5 t – 2= 0, t 1= 2, t 2 = -1/3. Следовательно,

(х 2 – х + 1)/ (х + 1) =2 или (х 2 – х + 1)/ (х + 1) = -1/3

х 1,2 = 3  13/2, x  .

Ответ: х 1,2 = 3  13/2.

Выполнила работу:

ученица 9 «ж» класса

филиала МБОУ «Горельская СОШ»

в с. Малиновка Тамбовского района

Коробанова Татьяна.

Руководитель: Четырина З. В.

учитель математики.

Введение

«Уравнения – это золотой ключ, открывающий все математические сезамы»

(С. Коваль )

Проблема

заключается в том, что на протяжении всех

лет обучения мы решаем уравнения, но

школьный курс алгебры предусматривает

ограниченный набор решений по данной теме.

Введение

Цель работы

выявление способов решения уравнений, отличных от изучаемых в

школьной программе

и их применение.

Введение

.

Задачи

Задачи

• изучить историю развития уравнений;

• изучить и проанализировать специальную литературу по проблеме исследования;

• найти информацию о способах решения рациональных уравнений;

• рассмотреть и применить на практике различные методы решения уравнений ;

Задачи

• создать банк заданий по теме исследования;
• создать буклет для одноклассников.

Введение

Объект исследования

Предмет исследования

Рациональные уравнения

Нестандартные методы рациональных уравнений

Введение

Методы исследования

• поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;
• практический «Методы решения рациональных уравнений;
• сравнение, анализ, полученный в ходе исследова ния.

Введение

Гипотеза:

если знать нестандартные методы решения рациональных уравнений, то это позволит повысить качество выполнения некоторых олимпиадных и тестовых заданий ОГЭ.

Введение

Практическая значимость исследования

Материал данного исследования имеет практическую значимость и будет полезен любознательным школьникам, а так же выпускникам школы.

Она позволит улучшить подготовку и расширить математический кругозор в решении уравнений.

Основные понятия

• Решить уравнение – значит найти все его корни или доказать, что корней нет.
• Целым уравнением с одной переменной называется уравнение, левые и правые части которого – целые выражения.

Основные понятия

• Дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причем хотя бы одно из них – дробным выражением.

Из истории рациональных уравнений

• Необходимость решать уравнения в древности была вызвана потребностью в умении делить доходы и имущество, вычислять площади земельных участков и стоимость товара, определялась развитием астрономии и самой математики ;

Из истории рациональных уравнений

еще 3-4 тыс. лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения.

Наибольший

успех

в развитии учения

достиг греческий

ученый

Диофант ( III в);

Из истории рациональных уравнений

• однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. В своей книге «Ал-джабар» описал способы

решения различных

уравнений,

в том числе

и уравнений

высших степеней;

Из истории рациональных уравнений

• итальянский математик Джироламо Кардано 16в. вывел формулу для решения любого кубического уравнения;
• Франсуа Виет 16 в. «отец алгебры» – открыл несколько способов решения уравнений 4-й и 5-й степени;
• труды французского

математика Эвариста Галуа

19 в.– по теории алгебраических

уравнений положили начало

развитию современной алгебры.

Методы решения рациональных уравнений

1. Простейшие

Решаются путем простейших упрощений –приведение к

общему знаменателю, приведению подобных членов и т.д.

2 .Группировка

Путем группировки слагаемых, применяя формулы

сокращенного умножения привести уравнение к виду, когда

слева записано произведение нескольких множителей, справа –

ноль. Затем приравниваем к нулю каждый множитель и решаем.

3. Подстановка

Ищем в уравнении некоторое повторяющееся выражение,

которое обозначаем новой переменной, тем самым упрощая вид

уравнения.

Методы решения рациональных уравнений

4.Подбор

При решении уравнений высших степеней рациональные корни

уравнения a n x n + a n – 1 x n – 1 + …+ a 1 x + a 0 = 0 ищем в виде p / q , где

p — делитель a 0 , q — делитель a n , p и q взаимно простые числа.

5. «Искусство»

Трудность решения в какой-то мере входит в само понятие задачи:

там, где нет трудности, нет и задачи. (Д. Пойа )

Т.е. решать задачи нестандартно, придумать «свой метод»,

догадаться что-то прибавить и отнять, выделить полный квадрат,

на что-то разделить и умножить и т.д.

0 Однородное Симметрическое Замена: Замена:" width="640"

Классификация рациональных уравнений

Возвратное

Биквадратное

Замена:

Замена:

x 2 = t,

t 0

Однородное

Симметрическое

Замена:

Замена:

Классификация рациональных уравнений

Уравнения вида

Замена:

Замена:

t = x 2 – (a + d )x

«Искусство»

1.Приём выделения квадрата двучлена.

Пример. Решить уравнение.

х 2 + 81х 2 /(9 + х) 2 = 40.

Решение: х 2 + 81х 2 /(9 + х) 2 = 40, О.Д.З. х  -9.

Воспользуемся формулой а 2 + b 2 = (а– b ) 2 + 2а b ,

(х – 9х/(9 +х)) 2 + 2х· 9х/(9 + х) = 40,

пусть х 2 /(9 + х)= t . Тогда t 2 + 18 t – 40 = 0

t 1 = -20; t 2 = 2. Получаем:

х 2 /(9 + х)= 2, или х 2 /(9 + х)= -20

х = 1  19 , корней нет.

Ответ: 1  19.

Методы решения рациональных уравнений

5. «Искусство»

То есть решать задачи нестандартно,

придумать «свой метод»,

догадаться что-то прибавить и отнять,

выделить полный квадрат,

на что-то разделить и умножить и т.д.

«Искусство»

2. Приём почленного деления.

Пример . Решить уравнение.

13 x /(2 x 2 + x +3) + 2 x /(2 x 2 –5 x +3) =6.

Решение:13 x / (2 x 2 + x +3) + 2 x / (2 x 2 –5 x +3) =6.

(:на x  0), обозначим: 2 x + 3 / x = t . Получаем:

13 / ( t + 1) + 2 / ( t – 5) = 6;

6 t 2 – 39 t + 33 = 0; t 1 = 1; t 2 = 5,5.

2 x + 3/ x =1; 2 x 2 – x +3=0; D = 1–24

2 x + 3/ x =5,5; 4 x 2 – 11 x + 6 = 0; x 1 = 2; x 2 = 0,75.

Ответ: x 1 = 2; x 2 = 0,75.

«Искусство»

3.Прибавить и отнять в уравнении.

Пример. Решить уравнение.

х 4 –2х 3 +х- 3/4 =0.

Решение: х 4 – 2х 3 + х - 3/4 = 0.

Прибавим и вычтем в левой части х 2 ,

выделим полный квадрат, получим:

х 4 – 2х 3 + х 2 – х 2 + х – 3/4 = 0,

(х 2 – х) 2 – (х 2 – х) – 3/4 = 0. Пусть х 2 – х = t ,

тогда t 2 – t –3/4=0, t 1 = -0,5; t 2 = 3/2.

х 2 – х = -0,5, или х 2 – х = 3/2

x  . x 1,2 = (1  7) / 2.

Ответ: (1  7) / 2.

Результаты

В процессе написания работы:

• изучены и обобщены научные сведения по теме «Рациональные уравнения»;

• рассмотрены основные способы решения рациональных уравнений;

Результаты

• выявлены приёмы, позволяющие понизить степень уравнения и тем самым упростить процесс решения;
• скомплектован банк задач на различные методы рациональных уравнений, представленных в приложении.

Заключение

• изучено большое количество математической литературы, освоение которой, позволило повысить уровень знаний по математике;
• рассмотрены различные способы решения рациональных уравнений;

Заключение

• приобретенные навыки будут использованы

при решении неравенств, систем неравенств и уравнений, а так же

при изучении математики

в старших классах

и сдачи экзаменов.

Шаблон

Заключение

Скажи мне, и я забуду.

Покажи мне, и я запомню.

Дай мне действовать самому,

и я научусь.

Литература

• 1. Г. И. Глейзер. «История математики в школе»
• 2. Карп А.П. Сборник задач по алгебре и началам анализа: Учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 1995. – 176 с.
• 3.Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 9 класс – 15-е изд., дороб. – М.: Просвещение, 2014г.
• 4. Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений / А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2013. – 215 с. : ил.
• 5. Петрушина С.Н., Жуковский Е.С. Математика для поступающих в вузы: Изд-во ТГУ им. Г.Р. Державина, 2004. 97с.
• 6. Письменный Д.Т. Готовимся к экзамену по математике. – Москва, Издательство «Айрис», 2005. – 136 с. : ил.
• Интернет-ресурс:
• 7. http://900igr.net/up/datai/83838/0003-003-.jpg
• 8. https://ds03.infourok.ru/uploads/ex/0de4/0004401b-e1bcc051/640/img10.jpg
• 9. http://mmetodika.narod.ru/page/urav2.htm

3.3.Симметрическое уравнение

• 3.3.Симметрическое уравнение

Уравнения a 0 x n + a 1 x n – 1 + … + a 1 x + a 0 = 0

называют симметрическим (коэффициенты

членов, равностоящие от концов, равны)

решаются подстановкой х +1/х = t .

• Уравнения a 0 x n + a 1 x n – 1 + … + a 1 x + a 0 = 0 называют симметрическим (коэффициенты членов, равностоящие от концов, равны) решаются подстановкой х +1/х = t .

Пример . 2 x 4 + 3 x 3 – 16 x 2 + 3 x + 2 = 0

• Пример . 2 x 4 + 3 x 3 – 16 x 2 + 3 x + 2 = 0

Решение. 2 x 4 + 3 x 3 – 16 x 2 + 3 x + 2 = 0

(:на x 2  0), т.е.2( x 2 + 1 / x 2 ) + 3( x + 1 / x )–16= 0,

обозначим x + 1 / x = t , получим:

2 t 2 + 3 t – 20 = 0, t 1 = – 4; t 2 = 5 / 2

x + 1 / x = – 4; x 2 + 4 x + 1 = 0; x 1,2 = –2  3,

x + 1 / x = 5 / 2; 2 x 2 – 5 x + 2 = 0; x 3 = 2;

x 4 = 1 / 2. Ответ: x 1,2 = –2  3; x 3 = 2; x 4 = 1 / 2.