Использование современных педагогических технологий в построении современного развивающего урока

Математика

Хорошайло Галина Васильевна - преподаватель математики и ИКТ, высшей категории

Государственное бюджетное образовательное учреждение среднего профессионального образования(ССУЗ)

К аслинского промышленно-гуманитарного техникума

«… знания можно предложить, но овладеть ими может и должен каждый самостоятельно»

А. Дистервег

Ход урока

• Организационный момент

Рефлексия:







2. Подготовка к изучению нового материала

Вопросы

• Что называют функцией?
• Как называется переменная Х?
• Как называется переменная Y?
• Что называется областью определения функции?
• Что называется множеством значения функции?
• Какая функция называется возрастающей?
• Какая функция называется убывающей?

3 .

.Применение производных к

исследованию функции.

УРОК №1-2

Возрастание и убывание функции

ФГОСТ : Знать : признаки возрастания и убывания функции

Уметь: исследовать функцию на монотонность

«Производная, Ваше Величество…»

Ах, госпожа производная,

Вы к нам на помощь пришли!

Вы честная и благородная,

Для функций свой штрих принесли.

Функции дифференцируя,

Получше мы их узнаем.

Особые точки и линии

По алгоритмам найдем.

К нулю приравняй производную

И знаки все верно расставь.

Где «плюс», там, конечно, положено

Функции той возрастать.

Где знак производной меняется,

В тех точках экстремумы есть.

Легко они определяются,

Вас благодарим, Ваша честь!

А функций узнать чтобы выпуклость,

Производную дважды считай.

Спасибо вам, Ваше Величество,

Что вы добрались и сюда!

О. Панишева

4. Изложение новой темы

0 на промежутке (а, в)=У. Тогда R=f’(x 0 )= tq α 0, а это значит, что касательная L к графику функции направлена вверх и поэтому график функций на этом промежутке «поднимается», т.е. функция f(x) возрастает. Y У=F(X) O X " width="640"

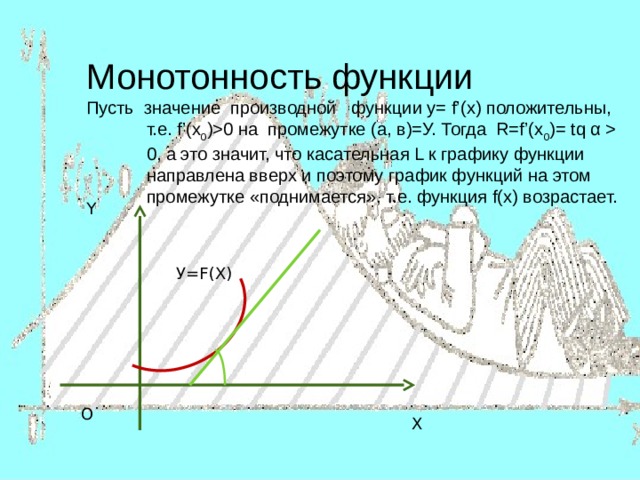
Монотонность функции

Пусть значение производной функции y= f’(x) положительны, т.е. f’(x 0 )0 на промежутке (а, в)=У. Тогда R=f’(x 0 )= tq α 0, а это значит, что касательная L к графику функции направлена вверх и поэтому график функций на этом промежутке «поднимается», т.е. функция f(x) возрастает.

Y

У=F(X)

O

X

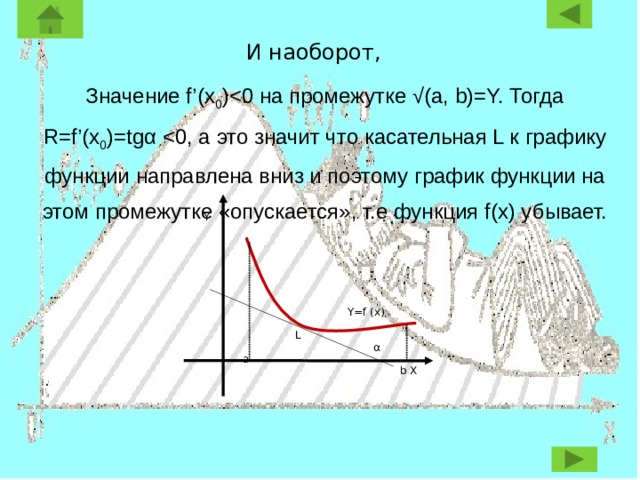
И наоборот,

Значение f’(x 0 )

Y

Y=f (x)

L

α

a

b X

0 на промежутке, то функция f(x) возрастает на этом промежутке. Графическое изображение: Схема : Y Y=f (x) f ' ‘ + f X O " width="640"

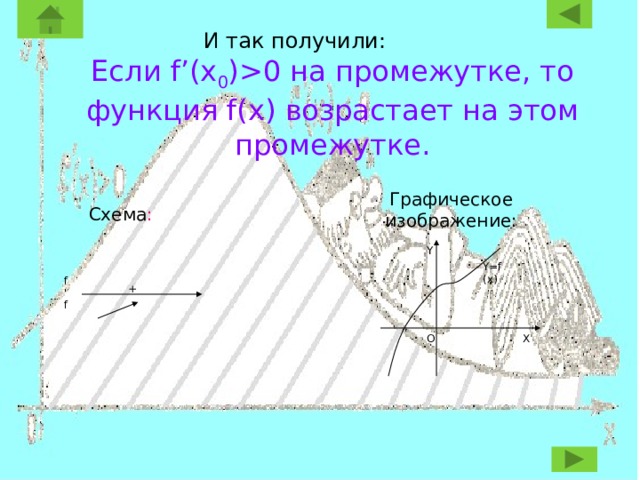
И так получили:

Если f’(x 0 )0 на промежутке, то функция f(x) возрастает на этом промежутке.

Графическое изображение:

Схема :

Y

Y=f (x)

f ' ‘

+

f

X

O

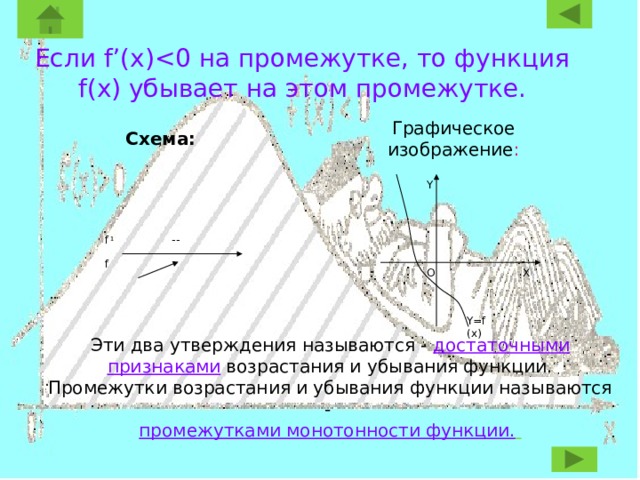
Если f’(x)

Графическое изображение :

Схема:

Y

f 1

--

f

X

O

Y=f (x)

Эти два утверждения называются - достаточными признаками возрастания и убывания функции.

Промежутки возрастания и убывания функции называются -

промежутками монотонности функции.

5. Первичное осмысление и применение изученного

0 и б) f’(x) Или 3(x-1)(x+1)0 3(x-1)(x+1)Решим это неравенство методом интервалов: 3(x-1)(x+1)=0 Откуда: x-1=0 или x+1=0 x=1 или x = -1 --- f 1 + + -1 f 1 X " width="640"

Пример №1.

Найти промежутки монотонности функции f (x)= x 3 -3x.

Решение:

1. Найти область определения f (x):

D ( ∞)=(-∞; ∞), т.к. это многочлен.

2. Найдите производную функции:

f’ (x)=(x 3 -3x)’= (x 3 )’-3(x)’= 3x 2 -3= 3(x 2 -1)= 3(x-1)(x+1)

3. Определить монотонность функции. Для этого решим неравенства:

А) f’(x) 0 и б) f’(x)

Или 3(x-1)(x+1)0 3(x-1)(x+1)

Решим это неравенство методом интервалов:

3(x-1)(x+1)=0

Откуда: x-1=0 или x+1=0

x=1 или x = -1

---

f 1

+

+

-1

f

1

X

F’(x) = 3(x-1)(x+1)

f’ (0) = 3(0-1)(0+1)

Таким образом, получили: F’(x) на (- ∞;-1] [1; ∞) и

F’(x) на [-1;1]

Схематически это выглядит так:

Y

Y=X 3 - 3X

-1 0 1

X

0, то функция y на (- ∞; ∞) или y постоянно. Графическое изображение схемы: Схема: Y Y=17x-5 + X X O " width="640"

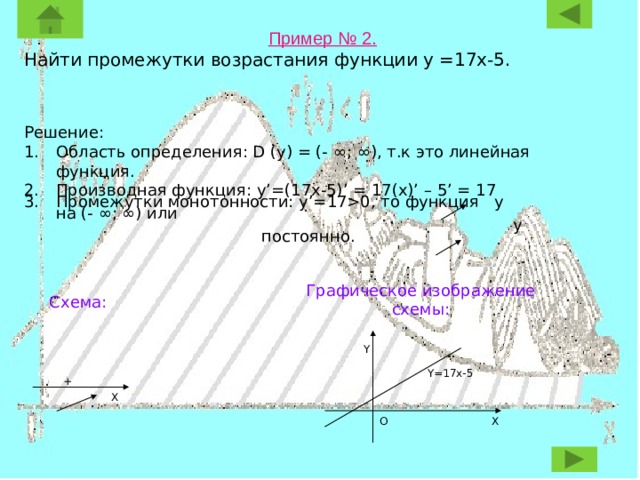
Пример № 2.

Найти промежутки возрастания функции y =17x-5.

Решение:

• Область определения: D (y) = (- ∞; ∞), т.к это линейная функция.
• Производная функция: y’=(17x-5)’ = 17(x)’ – 5’ = 17
• Промежутки монотонности: y’=170, то функция y на (- ∞; ∞) или

y постоянно.

Графическое изображение схемы:

Схема:

Y

Y=17x-5

+

X

X

O

Пример № 3.

По графику определить:

а)промежутки возрастания,

б) промежутки убывания.

Решение:

а)на (- ∞ ;-3] и [-0,5;3] функция y=f (x) возрастает.

б)на [-3;-0,5] и [3;4,5] функция y=f (x) убывает .

Y

Y=f (x)

X

-3 0 1 3 4,5

0 б) промежутки, где производная f’ (x) Y -4 0 1 X Решение: а) f’ (x) 0, если f (x) , следовательно, это промежуток [-2;1]. б) f’ (x) " width="640"

Пример №4

По графику определить:

а) промежутки, где производная f’ (x) 0

б) промежутки, где производная f’ (x)

Y

-4 0 1 X

Решение:

а) f’ (x) 0, если f (x) , следовательно, это промежуток [-2;1].

б) f’ (x)

0 и б) f’ (x) Ответ. Признаки и схемы монотонности: 1. f (x) ,если f’ (x) 0 2. f (x) ,если f’ (x) + X --- X " width="640"

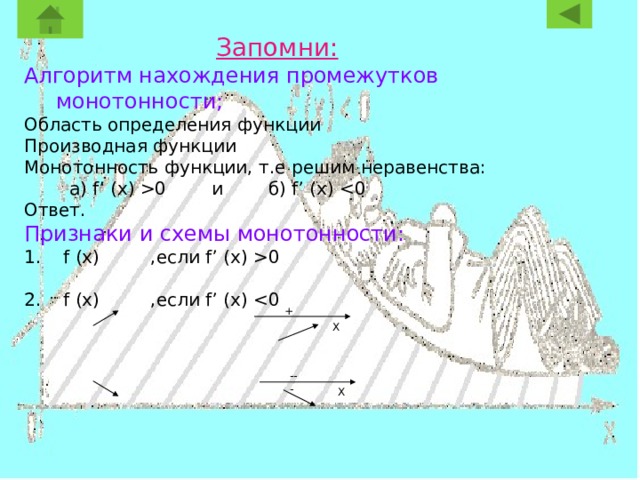
Запомни:

Алгоритм нахождения промежутков монотонности;

Область определения функции

Производная функции

Монотонность функции, т.е решим неравенства:

а) f’ (x) 0 и б) f’ (x)

Ответ.

Признаки и схемы монотонности:

1. f (x) ,если f’ (x) 0

2. f (x) ,если f’ (x)

+

X

---

X

В развитии дифференциального и интегрального исчисления главная роль принадлежала двум великим ученым – англичанину Исааку Ньютону и немцу Готфриду Вильгельму Лейбницу (1646-1716 ).

Историческая справка

Г.Лейбниц

И.Ньютон

Производная – одно из фундаментальных понятий математики. Оно возникло в XXVII веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к прямой. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время

Исчисление созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии. В частности, используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XXVII века. С помощью тех же методов математики изучали в XXVII и XXVIII веках различные кривые, нашли кривую, по которой быстрее всего падает материальная точка, научились находить кривизну линий.

Большую роль в развитии дифференциального исчисления сыграл Л. Эйлер, написавший учебник “Дифференциальное исчисление”.

Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX века французский математик О. Коши дал строгое построение дифференциального исчисления на основе понятия предела.

Применяемая сейчас система обозначений для производной восходит к Лейбницу и Лагранжу.

Эйлер Л.

О. Коши

Лагранж

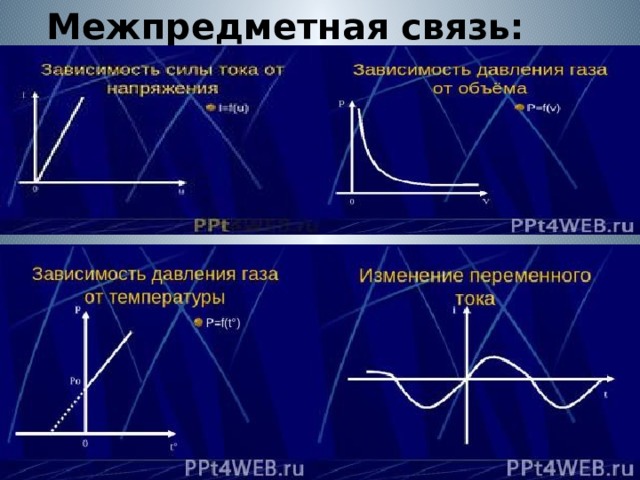
Межпредметная связь:

• Самостоятельная работа (уровневая),групповая
• Самостоятельная работа (уровневая),групповая
• Самостоятельная работа (уровневая),групповая
• Самостоятельная работа (уровневая),групповая
• Самостоятельная работа (уровневая),групповая
• Самостоятельная работа (уровневая),групповая
• Самостоятельная работа (уровневая),групповая

Групповая работа( в парах):

Задания

Для студентов 1 уровня : № 554 из учебного пособия Ш.А.Алимов и др. Алгебра и начала анализа, 10-11, Москва, «Просвещение»,1994

Для студентов 2 уровня : 1 группе - Варианты 10(5), 26(5)

2 группе - Варианты 16(4), 43(5)

3 группе – 18(5), 87(5) из сборника заданий для проведения письменного экзамена за курс средней школы 11 класс, Дрофа, Москва

Для студентов 3 уровня : 1 группе - 4.185, 4.187

2 группе – 4.188, 4.192 из сборника заданий для проведения письменного экзамена за курс средней школы 11 класс, Дрофа, Москва

Критерии оценки выполнения самостоятельной работы .

90-100% верно выполненных заданий - оценка «отлично»

80-90% верно выполненных заданий - оценка « хорошо»

70-80% верно выполненных заданий - оценка « удовлетворительно »

Менее 70% верно выполненных заданий - оценка « неудовлетворительно »

Ответы к решению заданий самостоятельной работы

Уровни заданий

1 уровень

1

2 уровень

а)y↓ на (-∞;1/2)

2.

y ↑на(1/2; ∞)

1группа: 1) y ↑на(- ∞;-2)ᴜ(3;∞)

3.

3уровень

б) y ↑на(0,3; ∞)

4.

в) y ↑на(-1; ∞)

2группа:1) y ↑на (-∞;0)ᴜ(1;+∞)

• y ↑на(-∞;-1 1/3)ᴜ(2;∞)

1группа: 1) y ↑на(-√2;0)ᴜ(√2;∞)

y↓ на(-∞; 0,3)

2) y↓ на(-∞;+∞)

2группа: 1) ) y ↑на (-∞;-1)ᴜ(1;∞)

y↓ на(-∞;-√2)ᴜ(0; √2)

y↓ на(-∞; -1)

• группа:1) y↓ на(-4;1)ᴜ(1;+∞)

г) y ↑на(-6; ∞)

2) y ↑на(-∞;+∞)

y↓ на (-1;0)ᴜ(0;1)

2) y↓ на (-1;7)

y↓ на(-∞; -6)

2)

6.Подведение итогов урока

Рефлексия на конец урока.







Домашнее задание : для студентов 1 и 2 уровня - № 555 из учебного пособия Ш.А.Алимов и др. Алгебра и начала анализа, 10-11, Москва, «Просвещение»,1994

Для студентов 3 уровня : Вариант 78(5) из сборника заданий для проведения письменного экзамена за курс средней школы 11 класс, Дрофа, Москва,

приготовить примеры (графики) возрастающих и убывающих функций

Спасибо за урок !

Решать, работать можно вечно.

Вселенная ведь бесконечна.

Спасибо всем нам за урок,

А главное, чтоб был он впрок!

Мне очень понравилось с вами работат ь