Инструкционная карта практического занятия №1
Тема занятия: «Решение задач на расчет количества выборок.».
Цель занятия: Научиться решать задачи на расчет количества выборок.
Для выполнения работы студент должен знать:
знать понятие случайного события и его виды (достоверное и невозможное, совместные и несовместные события)
знать понятие полной группы событий и пространства элементарных исходов
знать схему выборок с возвращением и без возвращения, с повторением и без повторения и знать соответствующие формулы для вычисления комбинаторных объектов
уметь вычислять факториалы и проводить действия с ними
уметь вычислять сочетания (с повторением и без повторений), размещения (с повторением и без повторений), перестановки (с повторением и без повторений)
знать основные свойства сочетаний и уметь применять их на практике.
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
Решить задачи на расчет количества выборок согласно своему варианту.
Обозначить событие А.
Найти число всевозможных исходов – n.
Найти число исходов, благоприятствующих наступлению события А – m.
Найти искомую вероятность 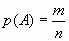 .
.
Вариант1
1.В урне находится 10 шаров, из них 6 белых и 4 черных шара. Вынули из урны 2 шара. Какова вероятность того, что оба шара - белые?
2. Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найти вероятность того, что набраны нужные цифры.
3. Из 30 экзаменационных билетов один учащийся не знает двух, а другой – трех билетов. Кому из них выгоднее брать билет первым и кому вторым?
4. восемь девушек, в том числе три сестры, водят хоровод. Какова вероятность того, что встав в круг наугад, сестры окажутся рядом?
Вариант2
1.В секретном замке на общей оси 4 диска, каждый из которых разделен на 5 секторов, на которых написаны различные цифры. Замок открывается, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.
2.В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки различны?
3. в коробке 90 годных и 10 дефектных шурупов. Какова вероятность того, что из 5 взятых наугад шурупов ровно 2 шурупа окажутся дефектными?
4. В связке 20 ключей, из которых только один подходит к данному замку. Найдите вероятность того, что для открывания замка придется испробовать ровно половину этих ключей?
Вариант3
Из всех трехзначных чисел наугад выбирают одно число. Чему равна вероятность того, что оно не делится хотя бы на одно из чисел 4 и 6?
Отдельные тома некоторого пятитомного издания располагаются на книжной полке в случайном порядке. Какова вероятность того, что хотя бы один том окажется не на своем месте?
Из общего числа 1000 лотерейных билетов 100 билетов- выигрышные. Какова вероятность того, что из 5 купленных билетов хотя бы один окажется выигрышным?
Белую и черную ладьи ставят на шахматной доске наугад. Какова вероятность того, что ладьи не будут бить друг друга?
Инструкционная карта практического занятия №2
Тема занятия: «вычисление вероятностей событий по классической формуле определения вероятности».
Цель занятия:
Для выполнения работы студент должен знать:
знать понятие случайного события и его виды (достоверное и невозможное, совместные и несовместные события)
знать понятие полной группы событий и пространства элементарных исходов
знать схему выборок с возвращением и без возвращения, с повторением и без повторения и знать соответствующие формулы для вычисления комбинаторных объектов
уметь вычислять факториалы и проводить действия с ними
уметь вычислять сочетания (с повторением и без повторений), размещения (с повторением и без повторений), перестановки (с повторением и без повторений)
знать основные свойства сочетаний и уметь применять их на практике.
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
Вычисление вероятностей событий по классической формуле определения вероятности.
1. Вероятность достоверного события равна единице: 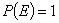 .
.
2. Вероятность объединения (суммы) несовместных событий равна сумме их вероятностей 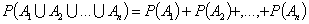
3. Вероятность невозможного события равна нулю: 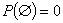
4.Вероятность события, противоположного событию А, равна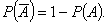
5. Теорема сложения вероятностей. Вероятность объединения произвольных событий равна сумме их вероятностей за вычетом вероятности произведения событий 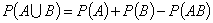 .
.
6. Условная вероятность. Если требуется найти вероятность события В при условии, что произошло некоторое другое событие А, то такую ситуацию характеризуют с помощью условной вероятности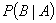 . Условная вероятность равна отношению вероятности произведения событий А и В к вероятности события А
. Условная вероятность равна отношению вероятности произведения событий А и В к вероятности события А 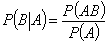
Пример решения:
В урне 5 белых, 20 красных и 10 черных шаров, не отличающихся по размеру. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым или черным?
Решение. Пусть событие А – появление белого или черного шара. Разобьем это событие на более простые. Пусть В1 – появление белого шара, а В2 – черного. Тогда, А=В1+В2 по определению суммы событий. Следовательно Р(А)=Р(В1+В2). Так как В1 и В2 – несовместные события, то по теореме о вероятности суммы несовместных событий (формула 4.3) Р(В1+В2) = Р(В1)+Р(В2).
Вычислим вероятности событий В1 и В2. В этом примере имеется 35 равновозможных (шары не отличаются по размеру) исходов опыта, событию В1 (появлению белого шара) благоприятствуют 5 из них, поэтому 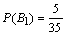 . Аналогично,
. Аналогично, 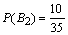 . Следовательно,
. Следовательно, 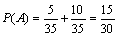 .
.
Вариант1
1.Ведутся поиски двух преступников. Каждый из них независимо от другого может быть обнаружен в течение суток с вероятностью 0,5. Какова вероятность того, что в течение суток будет обнаружен хотя бы один преступник?
2.Преступник имеет 3 ключа. В темноте он открывает дверь выбирая ключ случайным образом. На открытие каждой из дверей он тратит 5 сек. Найти вероятность того, что он откроет все двери за 15 сек.
3. стержень разломан в двух наугад выбранных точках.ю какова вероятность того, что из образовавшихся трех стержней можно составить треугольник?
Вариант2
1.Ведутся поиски двух преступников. Каждый из них независимо от другого может быть обнаружен в течение суток с вероятностью 0,5. После поимки одно из них, в связи с увеличением количества сотрудников, занятых в поисках, вероятность найти второго возрастает до 0,7. Какова вероятность того, что в течение суток будет обнаружены оба преступника.
2.В проведении операции по освобождению заложников участвуют 2 группы снайперов: 10 человек с винтовкой ОП21 и 20 человек с АКМ47. Вероятность поражения из ОП21 – 0,85, а АКМ47 – 0,65. Найти вероятность того, что при одном выстреле произвольного снайпера преступник будет поражен.
3. В семье двое детей. На мой звонок дверь открыл мальчик. Какова вероятность того, что другой ребенок в семье тоже мальчик?
Инструкционная карта практического занятия №3
Тема занятия: «Вычисление вероятностей сложных событий с помощью теорем умножения и сложения вероятностей».
Цель занятия: Научиться вычислять вероятности сложных событий с помощью теорем умножения и сложения вероятностей.
Для выполнения работы студент должен знать:
Теоремы вероятностей умножения и сложения.
Формулы вероятностей.
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
 Теорема1: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло, т.е. Р(АВ)= Р(А)РА(В).
Теорема1: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло, т.е. Р(АВ)= Р(А)РА(В).
Доказательство:
Пусть в результате опыта возможны N исходов, из них М благоприятствуют появлению события А, их этихМ- К исходов благоприятствуют событию В. Одновременному появлению событий А и В благоприятствуют L исходов из К.. По классической формуле имеем: Р(АВ)=L/N. Умножим и разделим на М:
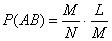
Первая дробь- вероятность наступления события А, вторая- вероятность события В, при условии, что А уже произошло, т.е. условная вероятность события В, что и требовалось доказать.
 Теорема2: Вероятность произведения двух независимых событий А и В равна произведению их вероятностей Р(АВ)=Р(А)Р(В).
Теорема2: Вероятность произведения двух независимых событий А и В равна произведению их вероятностей Р(АВ)=Р(А)Р(В).
Доказательство:
Т.к. события независимые, то верно равенство РА(В)=Р(В), тогда получим Р(АВ)=Р(А)Р(В).
Пример решения задачи (умножение)
По мишени стреляют три стрелка. Вероятности попадания соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что попадут все три.
Решение:
Пусть событие А- попал 1-й, В- 2-й и С-3-й. Эти события независимые, тогда применяя соответствующую теорему получим, что вероятность совместного появления всех трех событий равна: Р(АВС)=Р(А)Р(В)Р(С)= 0,7·0,8·0,9=0,504.
Решить задачу
В урне находятся 3 белых, 2 черных и 4 синих шара. Какова вероятность того, что первым будет вынут белый шар, вторым- синий, третьим- черный. Шары не возвращаются.
Теорема сложения вероятностей.
Доказательство:
Число всех исходов N, число исходов благоприятствующих событию А- К, событию В- L. Так как А и В несовместны, то ни один из этих исходов не может благоприятствовать А и В одновременно, т.е. А и В взаимно исключающие, следовательно число благоприятствующих исходов для события А+В равно К+L. Тогда вероятность равна
 Теорема2: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ).
Теорема2: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ).
Доказательство:
Всего исходов N, благоприятствующих событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В: 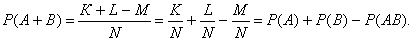
Пример решения задач (сложение)
Пример1. Найти вероятность суммы противоположных событий.
Решение: События А и А несовместны, следовательно Р( А +А ) = Р(А) + Р( А). Сумма двух противоположных событий есть событие достоверное, поэтому Р( А +А )= 1. Тогда Р(А) + Р( А ) =1. Отсюда следует : Р( А) = 1 - Р(А).
Решить задачи:
Вариант1
1.В урне 3 красных, 5 синих и 2 белых шара. Наудачу вынимают один шар. Какова вероятность того, что шар окажется цветным?
2. трехтомник стихотворений расположен на полке в случайном порядке. Найдите:
а) вероятность того, что первый том будет расположен на своем естественном (первоначальном) месте;
б) условную вероятность того, что первый том окажется на первом месте, при условии, что вторым на полке стоит второй том.
3. Из чисел 1,2,3,…,100 наугад выбирают одно число. Вычислить вероятность того, что выбранное число делится хотя бы на одно из чисел:
а)14 и 16 б) 4 и 6
Вариант2
1.В посевах пшеницы на поле 95% здоровых растений. Берут любые два растения. Найти вероятность того, что хотя бы одно из них здоровое.
2. в лифт девятиэтажного дома на первом этаже вошли четыре человека. Чему равна вероятность того, что на каком- нибудь этаже выйдет не менее двух из них?
3. В чулане десять разных пар ботинок. Случайно выбираются четыре ботинка. Определите вероятность того, что среди них найдется по крайней мере одна пара.
Инструкционная карта практического занятия №5
Тема занятия: «Вычисление вероятностей событий по формуле Бернулли.».
Цель занятия: Научиться вычислять вероятности событий по формуле Бернулли .
Для выполнения работы студент должен знать:
Теорему Бернулли
Формулу Бернулли.
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
Вычислить вероятность событий по формуле Бернулли согласно своему варианту.
Фрмула Бернулли
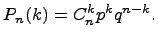
Пример решения задачи по формуле Бернулли:
Задача: Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?
Решение: Наивероятнейшее число побед k определяется из формулы
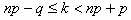
Здесь p =1/3 (вероятность победы), q = 2/3 (вероятность проигрыша), n - неизвестное число партий. Подставляя данные значения, получаем:
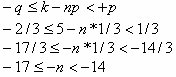
Получаем, что n = 15, 16 или 17.
Ответ: 15, 16, 17.
Вариант1
1.Из n аккумуляторов за год хранения k выходит из строя. Наудачу выбирают m аккумуляторов. Определить вероятность того, что среди них l исправных.
n = 100, k = 7, m = 5, l = 3.
2. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
3. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Вариант2
Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов;
в) хотя бы один элемент.
Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Ввриант3
В урне 20 белых и 10 черных шаров. Вынули подряд 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из четырех вынутых шаров окажется два белых?
Вероятность появления события А равна 0,4. Какова вероятность того, что при 10 испытаниях событие А появится не более трех раз?
Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0.8 и не зависит от номера выстрела. Требуется найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.
Вариант4
Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель.
Каждый день акции корпорации АВС поднимаются в цене или падают в цене на один пункт с вероятностями соответственно 0,75 и 0,25. Найти вероятность того, что акции после шести дней вернутся к своей первоначальной цене. Принять условие, что изменения цены акции вверх и вниз – независимые события.
Моторы многомоторного самолёта выходят из строя во время полёта независимо один от другого с вероятностью р. Многомоторный самолёт продолжает лететь, если работает не менее половины его моторов. При каких значениях р двухмоторный самолёт надёжней четырёхмоторного самолёта?
Инструкционная карта практического занятия №6
Тема занятия: «Решение задач на запись распределения ДСВ».
Цель занятия: Научиться решать задачи на запись распределения ДСВ .
Для выполнения работы студент должен знать:
Понятие случайных величин и их виды.
Закон распределения ДСВ.
Числовые характеристики и свойства ДСВ
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
Решить задачи на запись распределения ДСВ согласно своему варианту.
Рассмотрим случайную величину * 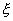 , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина
, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина 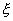 примет значение xi
примет значение xi
| 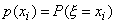
| (16) |
Такая случайная величина 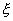 называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина
называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина 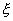 принимает всегда какое-либо значение из области ее изменения, то
принимает всегда какое-либо значение из области ее изменения, то
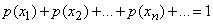
Пример решения задач:
Пример 1. Случайная величина 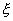 — число очков, выпадающих при однократном бросании игральной кости. Возможные значения
— число очков, выпадающих при однократном бросании игральной кости. Возможные значения 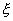 — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что
— числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что 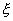 примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения.
примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения.
Решение: Таким образом, здесь закон распределения вероятностей есть функция р(х)=1/6 для любого значения х из множества {1, 2, 3, 4, 5, 6}.
Решить задачу:
Вариант1
Пусть случайная величина  - число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений
- число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений  состоит из 2-х чисел 0 и 1:
состоит из 2-х чисел 0 и 1:  =0, если событие A не произошло, и
=0, если событие A не произошло, и  =1, если событие A произошло. Таким образом,
=1, если событие A произошло. Таким образом,

Вероятность выхода изделия первым сортом равна 0,62. Составить ряд
распределения для числа изделий 1-го сорта из общего числа 5 изготовленных изделий. Найти его математическое ожидание и дисперсию.
Дан перечень возможных значений дискретной случайной величины Х: х1=1,х2=2, х3=3, а также известны математические ожидания этой величины и ее квадрата: М
(Х)=2,3; М (Х2)=5,9. Найти вероятности, соответствующие возможным значениям Х.
Вариант2
На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных?
В партии деталей 20% нестандартных. Наудачу отобраны 3 детали. Построить ряд распределения и функцию распределения числа нестандартных деталей среди отобранных. Найти математическое ожидание и дисперсию числа нестандартных деталей среди отобранных.
На пути движения автомобиля 6 светофоров, каждый из них или разрешает, или запрещает дальнейшее движение с вероятностью 0,5. Найдите закон распределения случайной величины X , равной числу светофоров, пройденных автомобилем до первой
остановки.
Инструкционная карта практического занятия №7
Тема занятия: «Вычисление характеристик ДСВ.».
Цель занятия: Научиться вычислять характеристики ДСВ
Для выполнения работы студент должен знать:
1.определение математического ожидания ДСВ, его сущность и свойства;
2.определение дисперсии ДСВ, её сущность и свойства;
3. определение среднеквадратического отклонения ДСВ, его сущность и свойства;
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
«Вычисление характеристик ДСВ»
Пусть дана случайная величина  а
а  . Если ряд
. Если ряд  сходится абсолютно, то его сумма называется математическим ожиданием (м.о.) с.в.
сходится абсолютно, то его сумма называется математическим ожиданием (м.о.) с.в.  .
.
Свойства математического ожидания:
 [
[ ] =
] =  , где
, где  - const;
- const;
 [
[ ] =
] =  [
[ ];
];
 [X
[X  Y] =
Y] =  [
[ ]
]  [
[ ];
];
 [X
[X Y] =
Y] =  [
[ ]
]  [
[ ], где
], где  и
и  - независимые с.в.
- независимые с.в.
Случайные величины  и
и  называются независимыми, если для любых
называются независимыми, если для любых  ,
,  имеет место равенство .
имеет место равенство .
Модой  д.с.в. называется ее наиболее вероятное значение.
д.с.в. называется ее наиболее вероятное значение.
Медианой  ряда значений
ряда значений 

 , которые с.в.
, которые с.в.  принимает с вероятностями
принимает с вероятностями  ,
,  , ...,
, ...,  соответственно, называется значение
соответственно, называется значение  с таким индексом
с таким индексом  , что
, что  и
и  Это означает, что приблизительно одинаково вероятно, продолжится ли процесс после медианы или закончится до нее.
Это означает, что приблизительно одинаково вероятно, продолжится ли процесс после медианы или закончится до нее.
Если математическое ожидание с.в.  существует, то оно называется начальным моментом
существует, то оно называется начальным моментом  [
[ ] порядка
] порядка  с.в.
с.в.  :
:
Поскольку  то из существования
то из существования  [
[ ] вытекает существование
] вытекает существование  [
[ ] и, следовательно, существование всех начальных моментов порядка меньше
] и, следовательно, существование всех начальных моментов порядка меньше 
Математическое ожидание с.в. является ее первым начальным моментом:

Начальные моменты, мода и медиана являются характеристиками положения случайной величины.
Начальный момент  [
[ ] д.с.в. можно находить как вес всего графа распределения с.в.
] д.с.в. можно находить как вес всего графа распределения с.в.  :
:

Пример решения задач:
Пример:Найти начальные моменты индикатора события  .
.
Решение.
Вариант1
1.Бросаем монету до тех пор, пока не выпадет решка; если это произойдет при  -м бросании, игрок получает из банка 2
-м бросании, игрок получает из банка 2 долларов. Сколько следует заплатить игроку за участие в игре, чтобы игра стала безобидной?
долларов. Сколько следует заплатить игроку за участие в игре, чтобы игра стала безобидной?
2. Вероятность, что лотерейный билет окажется выиграшным, равна 0,1. Покупатель купил 5 билетов. Найти распределение вероятностей для числа выигрышей у владельца этих 5 билетов.
3. Стрелок поражает мишень с вероятностью 0,7 при одном выстреле. Стрелок стреляет до первого попадания, но делает не более трех выстрелов. Найти распределение вероятностей для числа выстрелов.
Вариант2
1.Бросаем игральную кость до появления шестерки. Если это произойдет при  -м бросании, то игрок получит приз в
-м бросании, то игрок получит приз в  рублей. Какой вступительный взнос следует заплатить игроку, чтобы игра стала безобидной?
рублей. Какой вступительный взнос следует заплатить игроку, чтобы игра стала безобидной?
2. На перекрестке стоит автоматический светофор, в котором 1 минуту горит зеленый свет и 0,5 минуты – красный. Машина подъезжает к перекрестку в случайные моменты времени. Найти закон распределения времени ожидания у перекрестка.
3. Прибор комплектуется из двух деталей, вероятность брака для первой детали – 0,1, а для второй – 0,05. Выбрано 4 прибора. Прибор называется бракованным, если в нем есть хотя бы одна бракованная деталь. Построить закон распределения для числа бракованных приборов среди выбранных 4 приборов.
Вариант3
1. С конвейера поступили 4 детали. Вероятность брака для каждой детали равна 0,1. Детали проверяют одну за другой, пока не наберут две доброкачественные. Найти распределение вероятностей для числа проверенных деталей.
2. Каждая из 5 лампочек имеет дефект с вероятностью 0,1. Дефектная лампочка при включении сразу перегорает и ее заменяют новой. Построить закон распределения для числа опробованных ламп.
3. Среди 5 ключей два подходят к двери. Ключи пробуют один за другим, пока не откроют дверь. Найти распределение вероятностей для числа опробованных ключей.
Инструкционная карта практического занятия №8
Тема занятия: «Вычисление (с помощью свойств) характеристик функций от ДСВ.».
Цель занятия: Научиться вычислять характеристики функций от ДСВ.
Для выполнения работы студент должен знать:
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
Вычисление (с помощью свойств) характеристик функций от ДСВ. Решить согласно своему варианту.
Вариант1
1. Игральная кость подбрасывается до а) второго; б) третьего появления грани с номером «три». Найти среднее число подбрасываний.
Среди 10 деталей – три нужного размера. Детали извлекаются поочередно, пока не появятся две детали нужного размера, при этом делается не более 4-х проб. Найти распределение числа извлеченных деталей.
Стрелок поражает мишень с вероятностью 0,7 при одном выстреле. Стрелок стреляет до первого попадания, но делает не более трех выстрелов. Найти распределение вероятностей для числа выстрелов.
Вариант2
Вероятность, что лотерейный билет окажется выиграшным, равна 0,1. Покупатель купил 5 билетов. Найти распределение вероятностей для числа выигрышей у владельца этих 5 билетов.
В шестиламповом приемнике перегорела одна лампа. Лампы заменяют новыми одну за другой, пока приемник не заработает. Найти математическое ожидание и дисперсию числа замененных ламп.
В процессе производства изделие высшего качества удается получить только с вероятностью 0,2. С конвейера берутся наугад детали до тех пор, пока не будет взято изделие высшего качества. Найти математическое ожидание числа проверенных изделий.
Инструкционная карта практического занятия №9
Тема занятия: «Решение задач на формулу геометрического определения вероятности».
Цель занятия: Научиться решать задачи на формулу геометрического определения вероятности.
Для выполнения работы студент должен знать:
1.Формулы геометрического определения вероятности
Оборудование: методические указания к выполнению практических работ, бланки заданий, конспекты занятий, учебное пособие по математике.
Ход работы:
Решение задач на формулу геометрического определения вероятности согласно своему варианту.
Если число исходов некоторого опыта бесконечно, то классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события  есть отношение меры
есть отношение меры  (длины, площади, объема) к мере
(длины, площади, объема) к мере  пространства элементарных событий.
пространства элементарных событий.
Геометрическая вероятность события А определяется отношением:
,
Вариант1
Решить задачи:
1.В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.
2.В прямоугольник 5*4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
3. На плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r ( ). Найти вероятность того, что круг пересечет некоторую полосу.
). Найти вероятность того, что круг пересечет некоторую полосу.
Вариант2
1.Из отрезка [0, 2] на удачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам  .
.
2. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
3. В прямоугольник 5*4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
Вариант3
1. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
2. Из отрезка [0, 2] на удачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам  .
.
3. В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Инструкционные карты по теории вероятностей (0.22 MB)
Инструкционные карты по теории вероятностей (0.22 MB)
 0
0 2566
2566 201
201 Нравится
0
Нравится
0










