Получите свидетельство
Вход
Геометрическая прогрессия
Определение
Геометрической прогрессией называют числовую последовательность, каждый член которой a n , начиная со второго, равен произведению предыдущего члена a n-1 и некоторого постоянного числа q :
Число q называют знаменателем геометрической прогрессии.
1) геометрическая прогрессия, где 4*4=16 4*4=16 1 1 1*4=4 1*4=4 16*4=64 16*4=64 " width="640"
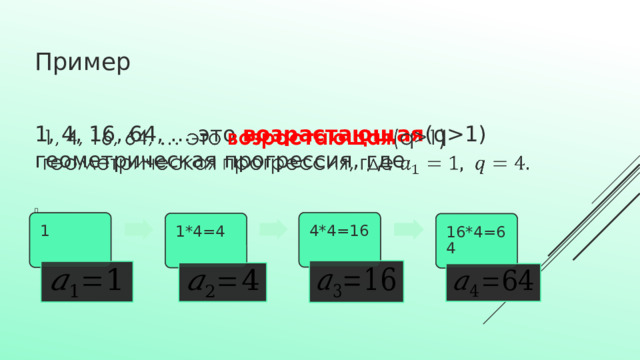
Пример
1, 4, 16, 64, … это возрастающая (q1) геометрическая прогрессия, где
4*4=16
4*4=16
1
1
1*4=4
1*4=4
16*4=64
16*4=64
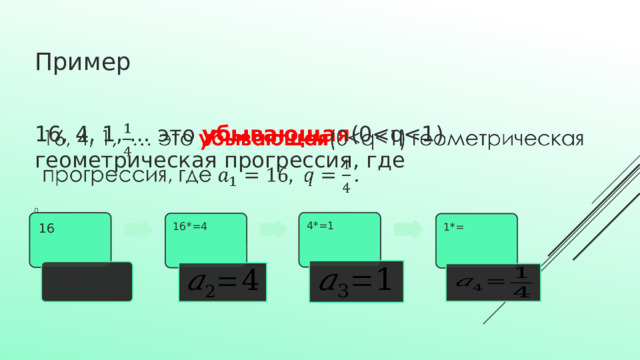
Пример
16, 4, 1, … это убывающая (0
4*=1
4*=1
16
16
16*=4
16*=4
1*=
1*=
- 6
- 6
- 6
- 6
Формула n-го члена геометрической прогрессии
a n = a 1 ·q n-1
Пример нахождения a 4 , где a 1 = 2, q = 3
пример
Найти знаменатель возрастающей геометрической прогрессии, первый член которой равен 2, пятый член равен 162
Решение:
162 = 2 *
Ответ: 3
Пример
Найти , где и
Решение:
Ответ:
Спасибо за внимание
Геометрическая прогрессия (247.32 KB)
0
685
10
Нравится
0
