Разработка урока по теме: «Формулы сокращённого умножения»
Тип урока: Рефлексия
Основная цель:
организовать самоконтроль умения применять формулы сокращённого умножения при выполнении заданий различного характера.
Демонстрационный материал:
1) формулы квадрата суммы и разности выражений
(а + b)2 = а2 + 2ab + b2
(а − b)2 = а2 − 2ab + b2
2) квадраты противоположных чисел (− а)2 = а2;
(− а – b)2 = (a + b)2;
(a – b)2 = (b – a)2
3) формула произведения разности и суммы (a – b)(a + b) = a2 – b2
4) формула разности квадратов а2 − b2 = (a – b)(a + b)
5) алгоритм нахождения произведения разности и суммы:
1. Найти квадрат первого выражения в разности.
2. Найти квадрат второго выражения в разности.
3. Записать разность квадратов.
6) алгоритм записи разности квадратов:
1. Первое выражение представить в виде квадрата выражения.
2. Второе выражение представить в виде квадрата выражения.
3. Записать произведение разности и суммы выражений.
7) куб противоположных чисел:
(− m)3 = − m3
(− х – у)3 = − (х + у)3
(х – у)3 = − (у − х)3
8) формула разность кубов а3 – b3 = (a – b)(a2 + ab + b2)
9) формула сумма кубов а3 + b3 = (a + b)(a2 - ab + b2)
10) правило записи произведения в виде суммы или разности кубов:
1. По двучлену определить формулу (сумма или разность кубов).
2. Представить каждый одночлен двучлена в виде степени третьей степени.
3. Найти третьи степени одночленов.
4. Записать результат в виде суммы или разности кубов.
11) правило представления суммы или разности кубов в виде произведения :
1. Представить каждый одночлен суммы (разности) в виде одночлена третьей степени.
2. Записать первый множитель: сумму (разность) оснований.
3. Записать второй множитель: неполный квадрат разности (суммы) оснований.
12) задания для актуализации знаний:
| Задание № 1 Запишите выражение как многочлен стандартного вида: а) (r − 1)2 – 3(r + 1)2; б) (z – t)2(z + t)2; в) 7(1 – с)3 + (с + 3)3 Задание №2. Найдите значение выражения при данном значении переменной: 125-(5-3х)(25+15х+9х2) при х= Задание № 3 Сократите дробь при допустимых значениях переменных: |
13) образец выполнения самостоятельной работы № 1 (ответы):
| Задание № 1: 10с2 – 28с + 51 Задание № 2: 7а – 6b Задание № 3: Ответ: { |
14) вопросы для этапа рефлексии:
|
Раздаточный материал:
1) самостоятельная работа № 1:
| Задание № 1 Запишите многочлен в стандартном виде: 4(с – 2)2 + (с + 3)(с2 – 3с + 9) – (с – 2)2 Задание № 2 Сократите дробь при допустимых значениях переменных: Задание № 3 Решите уравнение: 9(у + 1)2 + 3(у – 1)(у2 + у + 1) – 3(у3 + 3у2) = 48 |
2) эталон для самопроверки самостоятельной работы № 1:
| Задание № 1 4(с – 2)2 + (с + 3)(с2 – 3с + 9) – (с – 2)3 = = 4(с2 – 4с + 4) + (с3 + 33) – (с3 – 6с2 + 12с – 8) = = 4с2 – 16с + 16 + с3 + 27 – с3 + 6с2 – 12с + 8 = = 10с2 – 28с + 51 | 1.Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения. (а + b)2 = а2 + 2ab + b2 2. 1.В первом произведении определить формулу суммы кубов. (a + b)(a2 − ab + b2) = а3 + b3 2.2. Возвести каждый одночлен первого двучлена в третьею степень. 2.3. Найти третьи степени одночленов. 2.4. Записать результат в виде суммы кубов. 3. Записать куб разности в виде многочлена. (a − b)3 = a3 − 3a2b + 3ab2 − b3 |
| Задание № 2 | Разность квадратов двух выражений равна произведению их разности и их суммы. а2 − b2 = (a – b)(a + b) |
| Задание № 3 9(у + 1)2 + 3(у – 1)(у2 + у + 1) – 3(у3 + 3у2) = 48; Разделить всё уравнение на 3: 3(y + 1)2 + (y – 1)(y2 + y + 1) –(y3 + 3у2) = 16; 3(y2 + 2y + 1) + y3 – 1 – у3-3у2 = 16; 6y + 2 = 16; y = 14 : 6; y = Ответ: { | 1.Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения. (а + b)2 = а2 + 2ab + b2 2. 1.Во втором произведении определить формулу разности кубов. (a − b)(a2 + ab + b2) = а3 − b3 2.2. Возвести каждый одночлен первого двучлена в третью степень. 2.3. Найти третьи степени одночленов. 2.4. Записать результат в виде разности кубов. 3. Записать куб суммы в виде многочлена. (a + b)3 = a3 + 3a2b + 3ab2 + b3 4. Выполнить преобразования и найти корень уравнения |
3)Дополнительное задание:
Решите задачу: «Расстояние между городами А и В равно 120 км. Из города А в город В выехал велосипедист. Через 1 час из города А вслед за велосипедистом отправился мотоциклист, который обогнал велосипедиста и прибыл в город В на 3 часа раньше него. Чему равна скорость мотоциклиста, если она была в 3 раза больше скорости велосипедиста?»
4)Эталон выполнения дополнительного задания.
Пусть скорость х км/ч (х 0) скорость велосипедиста, тогда скорость мотоциклиста 3х км/ч.
Велосипедист затратил на дорогу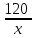
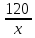 ч, а мотоциклист
ч, а мотоциклист 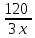
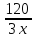 ч.
ч.
По условию известно, что велосипедист был в пути на 4 часа больше мотоциклиста:
х 0
3х - ?
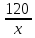
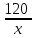 −
− 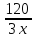
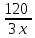 = 4;
= 4;
Разделить уравнение на 4
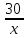
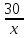 −
− 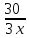
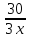 = 1;
= 1;
Сократить вторую дробь на 3
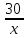
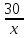 −
− = 1;
Вычесть дроби с одинаковыми знаменателями
= 1;
x = 20
20 0
20 ∙ 3 = 60 (км/ч)
Ответ: скорость мотоциклиста 60 км/ч.
4) таблица результатов:
| № (виды) заданий | Результат выполнения самостоятельной работы № 1 | Эталоны, в которых допущены ошибки | Результат работы над ошибками | Результат выполнения самостоятельной работы № 2 | ||||
| По образцу | По эталону для самопроверки | |||||||
| Задание № 1 |
|
|
|
|
| |||
| Задание № 2 |
|
|
|
|
| |||
| Задание № 3 |
|
|
|
|
| |||
|
| Результат выполнения | |||||||
|
|
| |||||||
5) самостоятельная работа № 2:
| Задание № 1 Запишите многочлен в стандартном виде: 2(а + 3)2 − (а − 4)(а2 + 4а + 16) + (а – 1)2 Задание № 2 Сократите дробь при допустимых значениях переменных: Задание № 3 Решите уравнение: (x + 3)(x2 – 3x + 9) − x(x – 5)(x + 5) = 102 |
6) эталон для самопроверки самостоятельной работы № 2:
| Задание № 1 2(а + 3)2 − (а − 4)(а2 + 4а + 16) + (а – 1)2 = = 2(a2 + 6a + 9) – (a3 – 43) + (a2 – 2a + 1) = = 2a2 + 12a + 18 – a3 + 64 + a2 – 2a + 1 = = − a3 + 3а2 +10a + 83 | 1.Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения. (а + b)2 = а2 + 2ab + b2 2.Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения. (а - b)2 = а2 - 2ab + b2 3.Во втором произведении определить формулу разности кубов. (a − b)(a2 + ab + b2) = а3 − b3 Возвести каждый одночлен первого двучлена в третьею степень. Найти третьи степени одночленов. Записать результат в виде разности кубов. |
| Задание № 2
|
Разность квадратов двух выражений равна произведению их разности и их суммы. а2 − b2 = (a – b)(a + b) |
| Задание № 3 (x + 3)(x2 – 3x + 9) − x(x – 5)(x + 5) = 102; x3 + 33 – x(x2 – 52) = 102; x3 + 27 – x3 + 25x = 102; 25x + 27 = 102; 25x = 102 – 27; 25x = 75; x = 75 : 25; x = 3 Ответ: {3} |
1. 1.В первом произведении определить формулу суммы кубов. (a + b)(a2 − ab + b2) = а3 + b3 1.2. Возвести каждый одночлен первого двучлена в третью степень. 1.3. Найти третьи степени одночленов. 1.4. Записать результат в виде суммы кубов. 2.1. Во втором произведении определить формулу суммы выражений на их разность. 2.2. Произведение суммы двух выражений на их разность равна разности их квадратов (a – b)(a + b) = а2 − b2 3. Выполнить преобразования и найти корень уравнения |
7) Тренировочное задание:
| 1. Возведите двучлены в квадрат: а) (3а + 1)2; б) (8 – 6х)2 2. Запишите выражения как многочлен стандартного вида: а) 6b(b + 5)(b – 5); б) (3х + у)(3х – у)2; в) (х + 3у)3 – 9х2у – 27ху2; г) (− 3r2 – s5)(9r4 – 3r2s5 + s10) |
8) подробный образец выполнения тренировочного задания:
| 1. а) (3а + 1)2 = 9a2 + 6a + 1 б) (8 – 6х)2 = 84 – 96x + 36x4 |
| 2. а) 6b(b + 5)(b – 5) = 6b(b2 − 25) = 6b3 − 150b; б) (3х + у)(3х – у)2 = (9x2 – y2)(3x – y) = 27x3 – 3xy2 – 9x2y + y3 в) (х + 3у)3 – 9х2у – 27ху2 = x3 + 9x2y + 27xy2 + 27y3 – 9х2у – 27ху2 = x3 + 27y3 г) (− 3r2 – s5)(9r4 – 3r2s5 + s10) = − ((3r2)3 + (s5)3) = − (27r6 + s15) = − 27r6 − s15 |
9) карточка для рефлексии:
| Понятия и способы действий | Знаю | Умею |
| Квадрат суммы двух выражений | | |
| Квадрат разности двух выражений | | |
| Разность квадратов двух выражений | | |
| Куб суммы двух выражений | | |
| Куб разности двух выражений | | |
Ход урока
1. Мотивация к коррекционной деятельности.
Цель:
1) организовать деятельность учащихся по установке тематических рамок: формулы сокращённого умножения;
2) сформулировать основную образовательную цель урока: подготовиться к контрольной работе;
3) создать условия для возникновения у ученика внутренней потребности включения в коррекционную деятельность.
Организация учебного процесса на этапе 1:
На доске- демонстрационный материал: формулы сокращенного умножения и алгоритмы, у учащихся на партах карточки для рефлексии.
− На следующем уроке вы будете писать контрольную работу. Какая задача стоит сегодня перед вами?
− Как вы будете работать на уроке?
− С чего начнёте работу?
2. Актуализация знаний и фиксация затруднения в индивидуальной деятельности.
Цель:
1) организовать воспроизведение способов действий (норм) – понятий, алгоритмов, свойств и т.д. во внешней речи: формулы сокращённого умножения;
2) организовать решение примеров на каждый способ действия;
3) актуализировать соответствующие мыслительные операции, внимание, память и т.д.:
сравнение, анализ, аналогия, обобщение;
4) организовать фиксацию актуализированных способов действий в речи;
5) организовать фиксацию актуализированных способов действий в знаках (эталоны);
6) организовать обобщение актуализированных понятий, правил, способов действий и т.д.;
7) мотивировать учащихся к написанию с. р. № 1 на применение способов действий, запланированных для рефлексивного анализа;
8) организовать выполнение с. р. № 1
9) организовать самопроверку учащимися своих работ по образцу и фиксацию полученных результатов (без исправления ошибок);
10 организовать мотивацию учащихся к сопоставлению работ по эталону для самопроверки с целью:
а) выявления места и причины затруднения;
б) самопроверки хода решения и правильности фиксации используемого эталона.
Организация учебного процесса на этапе 2:
На доску вывешивается карточка с заданиями для актуализации знаний
Задание № 1
Запишите выражение как многочлен стандартного вида:
а) (r − 1)2 – 3(r + 1)2; б) (z – t)2(z + t)2; в) 7(1 – с)3 + (с + 3)3
Задание № 2
Найдите значение выражения при данном значении переменной:
125-(5-3х)(25+15х+9х2) при х=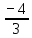
Задание № 3
Сократите дробь при допустимых значениях переменных:
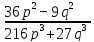
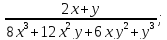
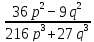 .
.
Каждое задание выполняет один ученик у доски, остальные работают в тетрадях. При выполнении заданий учащиеся называют формулы и алгоритмы и озвучивают каждый шаг.
Задание № 1
Запишите выражение как многочлен стандартного вида:
а) (r − 1)2 – 3(r + 1)2; б) (z – t)2(z + t)2; в) 7(1 – с)3 + (с + 3)3
Решение:
а) (r − 1)2 – 3(r + 1)2 =
Применим формулы квадрат суммы и квадрат разности двух выражений: квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения; квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения:
(r2 – 2r + 1) – 3(r2 + 2r + 1) =
Перед первой скобкой стоит знак «+», знаки в скобке меняться не будут, каждый член второго многочлена умножим на – 3:
r2 – 2r + 1 – 3r2 − 6r − 3 =
Приведём подобные слагаемые:
r2 – 2r + 1 – 3r2 − 6r − 3 = − 2r2 – 8r − 2
б) (z – t)2(z + t)2 =
Применим формулу разности квадратов: разность квадратов двух выражений равна произведению их разности и их суммы.
(z2 – t2)2 =
квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения и второго выражения плюс квадрат второго выражения:
z4 – 2z2t2 + t2
Задание №2.Найдите значение выражения при данном значении переменной:
125-(5-3х)(25+15х+9х2) при х=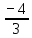 .
.
Решение. Применим формулу правило записи произведения в виде суммы или разности кубов.
По двучлену определяем, что необходимо применить формулу разности кубов, а выражения 5 и 3х возвести в третью степень:125-(125-27х3). Раскроем скобки. Учитывая, что перед скобкой стоит знак минус. 125-125+27х3=27х3. Подставляя вместо х значение переменной, получим -64.
Задание № 3
Сократите дробь при допустимых значениях переменных:
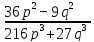
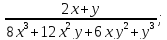
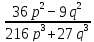 .
.
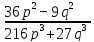
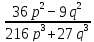 =
=
В числителе применим формулу разности квадратов, в знаменателе формулу суммы кубов:
=
Сократим дробь на 6p + 3q
− Что вы повторили?
− Сейчас вы будете работать самостоятельно, с какой целью вы будете выполнять самостоятельную работу?
Для самостоятельной работы учащимся раздаются карточки (С−1). На работу отводится 10 минут.
− Вы выполнили работу, что теперь вы должны сделать?
− С какой целью вы будете сопоставлять работу с образцом?
На доску вывешивается образец выполнения самостоятельной работы 1.
− Что теперь вы должны сделать?
− С какой целью вы будете работать с эталонами для самопроверки?
3. Локализация индивидуальных затруднений.
Цель:
организовать пошаговое сопоставление работ по эталону для самопроверки (работа проводится в группах):
а) организовать выявление учащимися места затруднения;
б) организовать выявление учащимися причины затруднения;
в) организовать фиксацию отсутствия затруднений в ходе решения и его обосновании.
Организация учебного процесса на этапе 3:
Каждый учащийся получает эталон для самопроверки самостоятельной работы № 1 .Учащиеся самостоятельно сопоставляют свои работы с эталонами для самопроверки, фиксируя результаты в карточках самопроверки.
Локализация затруднений проводится фронтально.
− Какие эталоны использовали при выполнении первого задания?
− У кого возникли затруднения в первом задании?
− В каких местах возникли затруднения?
− В чём причина возникших затруднений в первом задании?
Аналогичные вопросы задаются по второму и третьему заданию.
− У кого работа выполнена правильно?
− Какой вывод вы можете сделать?
4. Коррекция выявленных затруднений.
Цель:
1) организовать уточнение учащимися индивидуальных целей будущих действий;
2) на основе алгоритма исправления ошибок, организовать согласование плана достижения этой цели;
3) организовать реализацию согласованного плана действий:
для учащихся, допустивших ошибки:
а) организовать исправление ошибок с помощью предложенного эталона для самопроверки;
б) организовать выполнение учащимися заданий на способы действий, в которых допущены ошибки (часть заданий может войти в домашнюю работу);
в) организовать самопроверку заданий;
для учащихся, не допустивших ошибки:
4) организовать выполнение учащимися заданий более высокого уровня сложности по данной теме, заданий пропедевтического характера, или заданий требующих построения новых методов решения.
Организация учебного процесса на этапе 4:
− Что дальше будут делать те, кто выяснил, что затруднений нет? (Мы будем работать с дополнительными заданиями.)
− Посмотрите на задания и сформулируйте цель своей деятельности.
− Сформулируйте цель своей дальнейшей работы, те, у кого затруднения зафиксированы.
Учащиеся самостоятельно работают над ошибками. Для тренинга им предлагаются карточки с тренировочными заданиями .
Для самопроверки учащимся, которые работали с тренировочными заданиями раздаются карточки с подробными образцами.
В конце работы подводится результат.
− Кому удалось выполнить задания для тренинга без ошибок?
5. Обобщение затруднений во внешней речи.
Цель:
1) организовать обсуждение типовых затруднений в группах;
2) организовать проговаривание формулировок способов действий, которые вызвали затруднение.
Организация учебного процесса на этапе 5:
− В каких местах были допущены ошибки?
− На какие эталоны были допущены ошибки?
Эталоны, при использовании которых были допущены ошибки, озвучиваются.
6. Самостоятельная работа с самопроверкой по эталону.
Цель:
для учащихся, допустивших ошибки:
1) организовать выполнение с. р. № 2, аналогичной с. р. № 1 (учащиеся выбирают задания только на способы действий, в которых были допущены ошибки);
2) организовать самопроверку учащимися своих работ по эталону для самопроверки и знаковую фиксацию результатов;
3) организовать фиксацию преодоления возникшего ранее затруднения;
для учащихся, не допустивших ошибки:
организовать самопроверку учащимися заданий требующих построения новых методов решения или заданий пропедевтического характера по подробному образцу.
Организация учебного процесса на этапе 6:
− Кто будет выполнять вторую самостоятельную работу? (Те, кто допустил ошибки в первой самостоятельной работе.)
− С какой целью вы будете выполнять вторую самостоятельную работу?
− Как вы будете работать со второй самостоятельной работой? (Мы выполним только те задания, которые выполнили неправильно.)
Для работы учащимся предлагаются карточки самостоятельная работа №2. На работу отводится 5 минут. После выполнения работы учащиеся сопоставляют свои работы с эталоном для самопроверки самостоятельной работы №2, фиксируют результаты в таблице.
Учащиеся, которые работали с дополнительными заданиями, проводят самопроверку по подробному образцу решения дополнительного задания.
− Кто справился с затруднениями в задании 1?
− Кому удалось исправить ошибки в задании 2?
− Кому удалось правильно выполнить задание 3?
− С какими заданиями справились те, кто работал с дополнительными заданиями?
− В каких заданиях вы столкнулись с затруднениями?
− Вы смогли справиться с затруднениями, что вам в этом помогло?
7. Включение в систему знаний и повторение.
Цель:
тренировать умение решать задачи на движение
Организация учебного процесса на этапе 7:
− А теперь я предлагаю решить задачу.
Карточка с текстом задачи вывешивается на доску (Д−19).
Задание выполняется у доски с комментарием.
Пусть скорость автобуса х км/ч (х 0), а скорость автомобиля 4х км/ч. Автобус был в пути ч, а автомобиль
ч. По условию известно, что автобус был в пути на 8 ч больше:
4х - ?
х 0
;
Разделим всё уравнение на 8:
;
Вторую дробь сократим на 4:
;
Найдём разность двух дробей с одинаковыми знаменателями:
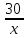
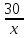 = 1;
= 1;
x = 30
30 0
30 ∙ 4 = 120 (км/ч)
Ответ: скорость автомобиля 120 км/ч
8. Рефлексия деятельности на уроке.
Цель:
1) организовать фиксацию степени соответствия поставленной цели и результатов деятельности;
2) организовать вербальную фиксацию причин (алгоритмов, правил, понятий и т.д.) возникших на уроке затруднений;
3) организовать вербальную фиксацию способа исправления возникших ошибок (алгоритм исправления ошибок);
4) организовать фиксацию неразрешенных на уроке затруднений как направление будущей деятельности;
5) организовать оценивание учащимися собственной работы на уроке;
6) организовать обсуждение и запись домашнего задания.
Организация учебного процесса на этапе 8:
− Что необходимо сделать в конце работы?
На доску вывешивается карточка с вопросами
− Обсудите в группах предложенные вопросы.
− А теперь каждый проанализируйте свою работу на уроке.
Учащиеся работают с карточками рефлексии.
Домашнее задание:
| Задачник №№ 28.50,28.51,28.52 |
6

 Получите свидетельство
Получите свидетельство Вход
Вход


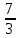 }
}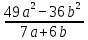
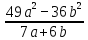
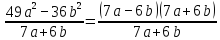 = 7a – 6b
= 7a – 6b








 Формулы сокращенного умножения. (36.14 KB)
Формулы сокращенного умножения. (36.14 KB)
 0
0 695
695 6
6 Нравится
0
Нравится
0









