"Элементы комбинаторике"

Kombinatorika elementlari

GULISTON DAVLAT UNIVERSITETI MATEMATIKA TA’LIM YO‘NALISHI 2-KURS TALABASI QO‘SHMURADOV LAZIZJON JUMABOY O‘G‘LI

Kombinatorika elementlari.

Kombinatoriyaga doir masalalarni yechishda dastlab 3 xil holatni o’rganib olamiz.

1. Bir-biriga bog’liq bo’lmagan holatlar.

2. Bir-biriga bog’liq bo’lgan holatlar.

3. Aralash holatlar.

1-Masala

Kiyim shkafida 3 xil kiyim bor 4 ta kostyum, 5 ta kofta, 6 ta yubka. Shkafni bir martta ochganda bitta kiyim olish imkoniyati bor bo’lsa, nechta urinishda kiyimlarni hammasini olish mumkin?

4 + 5 + 6 = 15

Bir-biriga bog’liq bo’lmagan jarayonda qo’shish amali bajariladi.

2-Masala

Kiyim shkafida 5 ta kastyum va 6 ta yubka bor. Kostyum va yubkani niche xil usulda kiyishi mumkin?

5 × 6 = 30

1-masala shartini o’zgartiramiz.

Kiyim shkafida 4 ta kostyum, 5 ta kofta, 6 ta yubka bor. Bu kiyimlarni hammasini necha xil usulda kiyish mumkin?

4 × 5 × 6 = 120 ta

Bir-biriga bog’liq bo’lgan holatlarda berilgan miqdorlar kupaytiriladi.

3-Masala

Idishda 5 ta anor? 6 ta olma? 7 ta nok bor. Ushbu mevalarni 2 tadan qilib? Boshqa idishchalarga joylashtirish kerak.

Buni necha xil usulda amalga oshirish mumkin?

A - 5 ta AO = 5 × 6 = 30 ta

O - 6 ta AN = 5 × 7 = 35 ta

N - 7 ta ON = 6 × 7 = 42 ta

Jami: 30 + 35 + 42 = 107 ta

Aralash holatda ko’paytmalar qo’shiladi.

4-Masala

Fazliddin uyidan maktabgacha 2 xil yo’l bilan, maktabdan do’kongacha 3 xil yo’l bilan borishi mumkin.fazliddin uyidan do’konga necha xil yo’l bilan borishi mumkin?

2 × 3 = 6

5-Masala

Nizom toqqa 7 xil usul bilan chiqishi mumkin? Lekin qaytishida chiqqan yo’lidan qaytishi mumkin emas. Nizomda tog’dan tushish uchun necha xil yo’l bor?

6-Masala

A

3

3

B

C

2

D

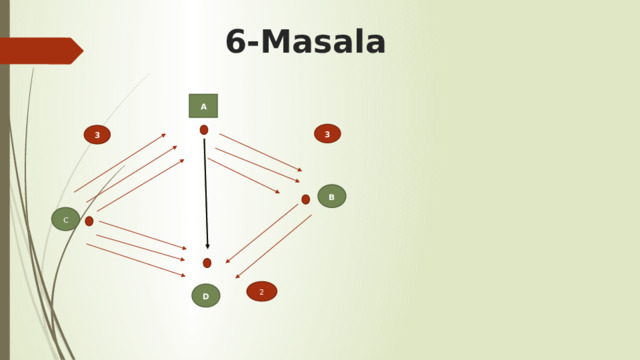
Chizmadagi C nuqtadan D nuqtaga necha xil usulda boorish mumkin?

C D

CD – 3 xil

CABD – 3 × 3 × 2 = 18 ta

CAD – 3 × 1 = 3 ta

3 + 18 + 3 = 24

Javob: 24 xil usul bor.

7 -Masala

Sinf doskasida Ot so’z turkumiga tegishli 10 ta, Fe’l so’z turkumiga tegishli 6 ta, Sifat so’z turkumiga tegishli 9 ta so’z bor. Har biridan bittadan olib gap tuzish topshirig’I berildi. O’quvchi nechta gap tuzishi mumkin?

10 × 6 × 9 = 540

8 -Masala

Nodir “Yulduz” oshxonasiga tushlik uchun bordi. Oshxona taomnomasida 3 xil somsa, 4 xil suyuq taom, 5 xil quyuq taom bor ekan. Nodir birdaniga uch turdagi taomdan buyurtma bermoqchi, necha xil usulda buyurtma qilish mumkin?

3 × 4 × 5 = 60 xil

O’ R I N L A SH T I R I SH M A S A L A L A R I

Testlarimizda eng ko’p uchraydigan savollarni ko’rib chiqamiz.

1 -Masala

3,6,7,9 raqamlaridan nechta to ’ rt xonali son tuzish mumkin? (ixtiyoriy)

3 3 3 3

6 6 6 6

7 7 7 7

9 9 9 9

4 × 4 × 4 × 4 = 256 ta son tuzish mumkin

2 -Masala

0,7,8,9 raqamlaridan nechta to’rt xonali son tuzish mumkin?

(ixtiyoriy).

7 0 0 0

8 7 7 7

9 8 8 8

9 9 9

3 × 4 × 4 × 4 = 192 ta

3 -Masala

0,1,2,7,9 raqamlaridan nechta uch xonali son tuzish mumkin? (ixtiyoriy)

1 0 0

2 1 1

7 2 2

9 7 7

9 9

4 × 5 × 5 = 100 ta usul bor

4-Masala

5,7,8,9 raqamlaridan nechta to’rt xonali son tuzish mumkin?

(raqamlar takrorlanmasin)

5 7 8 9

7 8 9

8 9

9____________________________________________

4 3 2 1

P = n !

4 × 3 × 2 × 1 = 24. n = 4.

4! = 1 × 2 × 3 × 4 = 24

5-Masala

0,1,6,7,8 raqamlaridan nechta to’rt xonali son yozish mumkin?

1 0 6 7

6 6 7 8

7 7 8

8 8

_____________________________________________

4 × 4 × 3 × 2 = 96 ta

6-Masala

1,3,7,8 raqamlaridan nechta to’rt xonali son tuzish mumkin?

(raqamlar takrorlanmasin)

8

3 × 2 × 1 × 1 = 6 ta Bu masalani yechish uchun 2 bo’linishlik shartini kiritamiz. Ya’ni son2 ga bo’linishi uchun u juft bo’lishi kerak!

Demak 6 ta 2 ga bo’linadigan.

7-Masala

“ BARNO” so’zida harflar o’rnini almashtirib, nechta so’z hosil bo’ladi?

5 × 4 × 3 × 2 × 1 = 120

p = 5 ! = 1 × 2 × 3 × 4 × 5 = 120

harflarni o’rnini almashtirib nechta so’z hosil qilish mumkin degan savollar uchraganida, eng qulay usul bu dan foydalanishdir.

P=n!

8-Masala

9-Masala

10-Masala

Umidda jami 3 ta matematika va 2 ta fizika darslik bor. Umid kitoblarni shunday joylashtirishi kerakki, har qanday holatda fizika kitoblari yonma-yon tursin.

Yechish:

2 ta fizikani bitta deb qaraymiz

3ta matematika, 1 ta fizika

4 × 3 × 2 × 1 = 24 ta

F × F × M × M × M

Jami: 24 × 2 = 48 ta