Булевы функции

В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п. Так или иначе, область определения – непрерывное множество. В курсе дискретной математики изучаться должны функции, область определения которых – дискретное множество*. Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов.* Так мы и приходим к понятию булевой функции.

Булевы функции

Определение 1

• Булевой функцией от n аргументов называется функция f из n-ой степени множества { 0, 1 } в множество { 0, 1 }.

таблица следующего вида:

функция “отрицание”

Определение 2

• Переменная x i называется фиктивной (несущественной) переменной функции f(x 1 ,···,x n ), если

f(x 1 ,···,x i-1 ,0,x i+1 ,···,x n ) = f(x 1 ,···,x i-1 ,1,x i+1 ,···,x n )

для любых значений x 1 ,···,x i-1 ,x i+1 ,···,x n . Иначе переменная x i называется существенной.

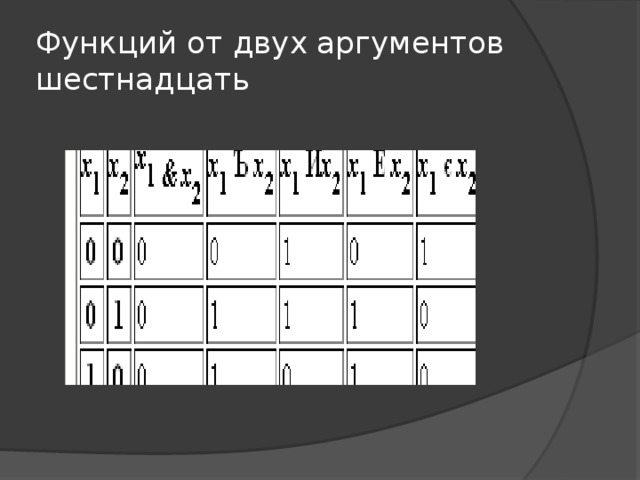
Функций от двух аргументов шестнадцать

бинарные операции

• x 1 & x 2 называется конъюнкцией
• x 1 Ъ x 2 – дизъюнкцией (V)
• x 1 Й x 2 – импликацией (→)
• x 1 є x 2 – эквивалентностью (~)
• x 1 Е x 2 – суммой по модулю 2 (⊕)
• x 1 | x 2 – штрихом Шеффера.

Конъюнкция переменных x и y

В табл. 5 представлены все 4 функции от одной переменой х

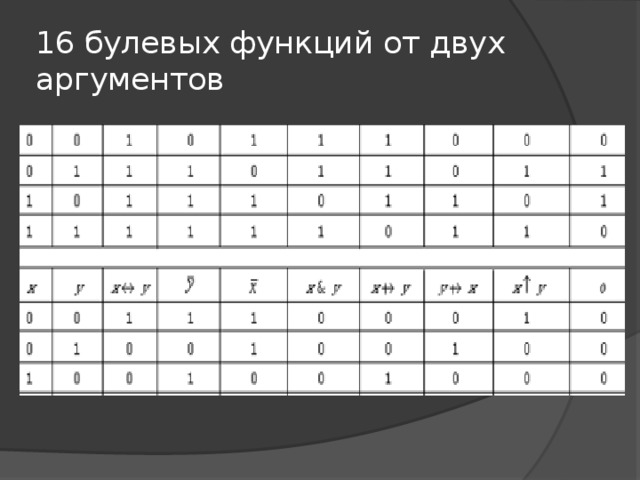
16 булевых функций от двух аргументов

общепринятые названия некоторых из этих функций

• Функция x → y называется импликацией.

• Функция x ↔ y называется эквиваленцией.

• Функция x ⊕ y называется сложением по модулю 2.

• Функция x | y называется операцией Шеффера (или штрихом Шеффера).

• Функция x ↑ y называется операцией Пирса (или стрелкой Пирса).

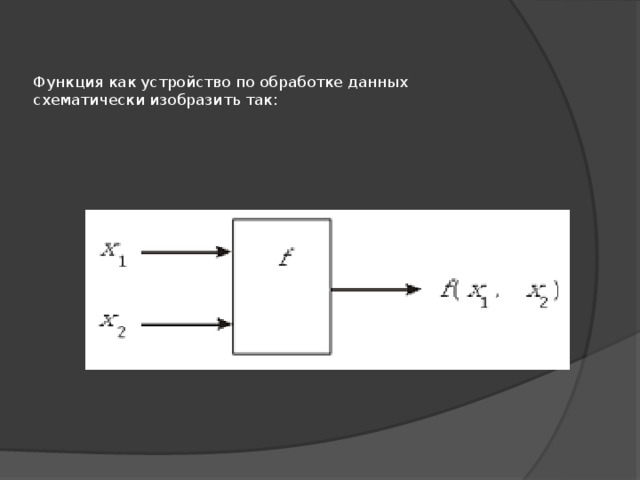
Функция как устройство по обработке данных схематически изобразить так:

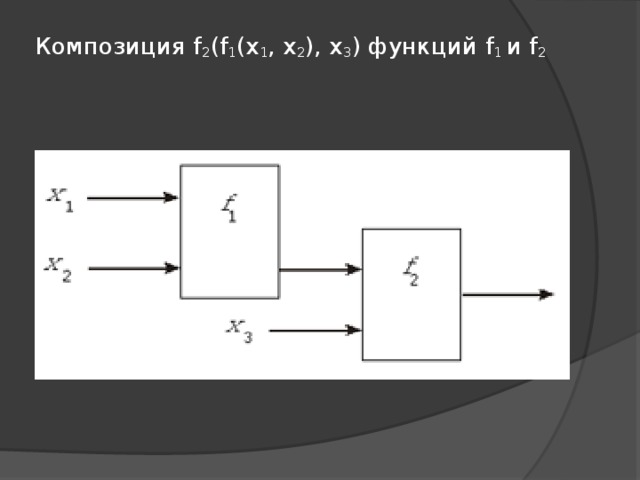
Композиция f 2 (f 1 (x 1 , x 2 ), x 3 ) функций f 1 и f 2

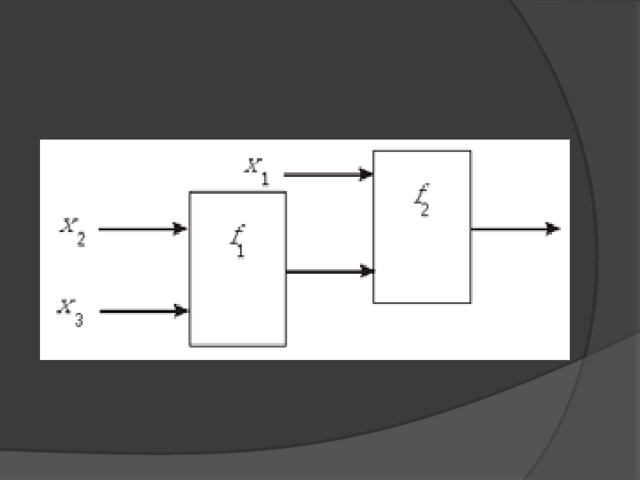
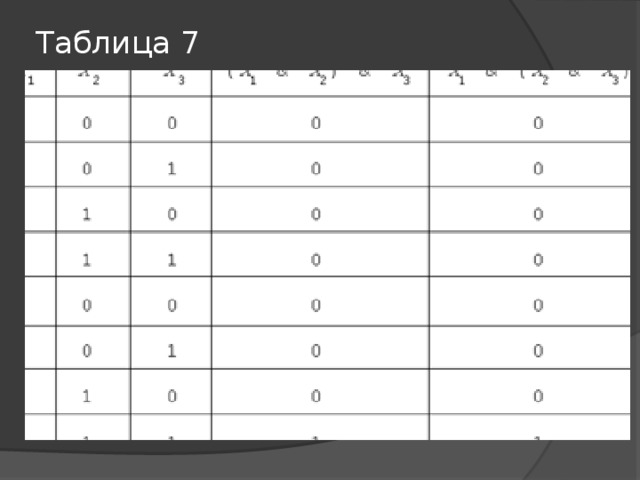
Таблица 7

Тождества алгебры булевых функций

Теорема 1

• Любая формула равносильна некоторой формуле в дизъюнктивной нормальной форме и некоторой формуле в конъюнктивной нормальной форме.

Тогда F будет представлена в одном из следующих видов:

Вопросы и задания

• а) Проверьте выполнение законов де Моргана.

  б) Проверьте выполнение тождеств 20–25.

2. Докажите тождества:

3. а) Преобразуйте в дизъюнктивную нормальную форму выражение

б) Преобразуйте то же выражение в конъюнктивную нормальную форму