Аксиомы стереометрии. Взаимное расположение двух прямых в пространстве, прямой и плоскости. Взаимное расположение плоскостей

Прямые и плоскости в пространстве

Колесникова А.С.

Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Вместе с этими фигурами рассматриваются геометрические тела и их поверхности.

Представление плоскости нам дает любая гладкая поверхность. Она безгранична.

• точки обозначаются прописными латинскими буквами: А, В, С и т. д.
• прямые – строчными латинскими буквами: а, b, с и т. д. или двумя большими латинскими буквами: АВ, ВС и т. д.
• плоскости – греческими буквами: α, β, γ и т. д.

Аксиомы

А1:  Через 3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

А2:  Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Если прямая и плоскость имеют одну общую точку, то говорят, что они  пересекаются.

А3:  Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой.

В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии.

Следствия из аксиом

Теорема 1:  Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Дано:

Доказательство:

а – прямая,

точка М ∉ а.

Доказать:

1) существует α: а  α.

2) α – единственная.

Теорема 2 : Через две пересекающиеся прямые проходит плоскость, и, причём только одна.

Доказательство:

Дано:

а ∩ b в точке М

Доказать:

существование плоскости

α, а α, b  α.

Задания

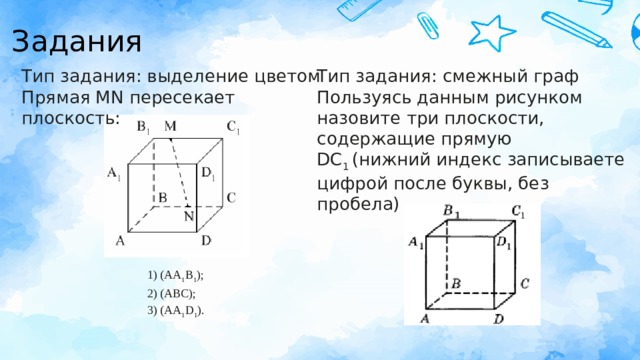
Тип задания: смежный граф

Тип задания: выделение цветом

Пользуясь данным рисунком

Прямая MN пересекает плоскость:

назовите три плоскости, содержащие прямую DС 1  (нижний индекс записываете цифрой после буквы, без пробела)

1) (АА 1 В 1 );

2) (ABC);

3) (AA 1 D 1 ).

Параллельные прямые

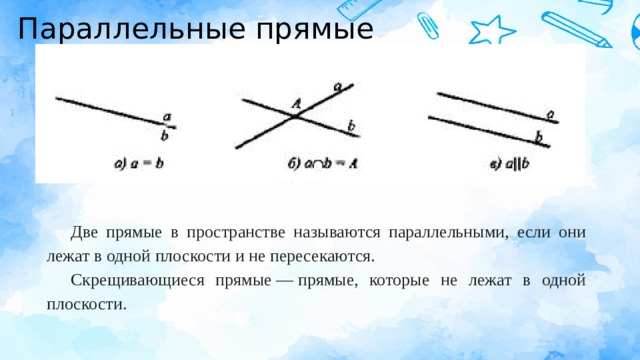
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

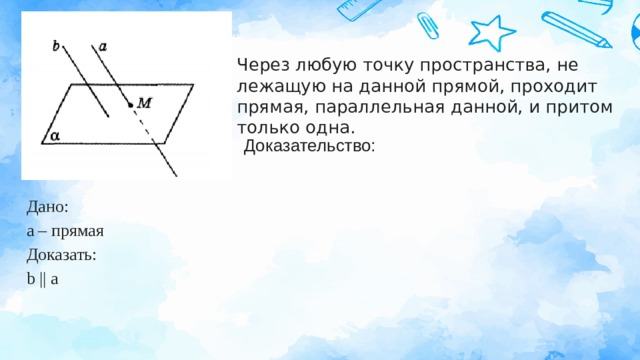
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Доказательство:

Дано:

а – прямая

Доказать:

b || a

Определение.  Два отрезка называются параллельными, если они лежат на параллельных прямых.

Аналогично определяется параллельность отрезка и прямой, а так же параллельность двух лучей.

Лемма.  Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Доказательство:

Теорема.  Если две прямые параллельны третьей прямой, то они параллельны.

Дано: 

Доказательство:

a ∥ c и b ∥ c

Доказать:

a ∥ b

Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

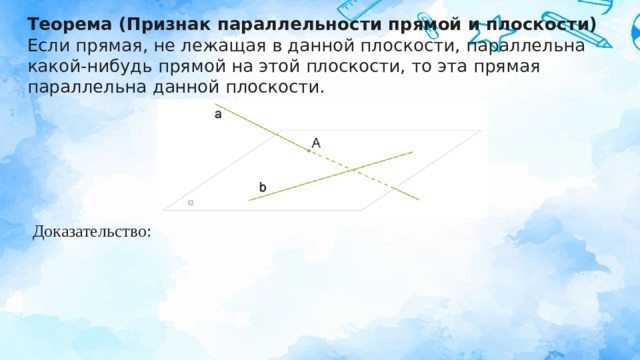
Теорема (Признак параллельности прямой и плоскости) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости. 

Доказательство:

Существует еще два утверждения, которые используются при решении задач:

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

Задания

Решение:

Дано:

∆ АВС

КМ − средняя линия,

КМ=5;

ACFE- параллелограмм.

Найти: EF

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

• АВ=2 см АВ=4 см АВ=5 см АВ=10 см
• АВ=2 см
• АВ=4 см
• АВ=5 см
• АВ=10 см