Часто бывает полезно знать, есть ли некоторая связь между изучаемыми величинами и, если есть, то какова она.
Чтобы наглядно представить соотношение данных между собой, используют диаграммы.
Диаграммы часто встречаются в газетах, журналах, книгах. Они иллюстрируют соотношение и изменение различных величин.
Например, столбиковые диаграммы применяются тогда, когда нужно увидеть, как меняется одна и та же величина со временем. Также столбиковые диаграммы используются для наглядного сравнения разных, но близких по смыслу величин.

Обратите внимание, на подпись, которая помогает нам разобраться в диаграмме. Она называется легендой диаграммы.

Круговая диаграмма показывает, как целое делится на части в виде секторов круга, углы которых пропорциональны долям единого целого.

При построении круговой диаграммы не нужно откладывать углы с большой точностью. Так как небольшая погрешность не мешает правильно воспринимать диаграмму.
Главными достоинствами круговой диаграммы являются наглядность восприятия и быстрота построения.
Для графического изображения рассеивания данных применяются диаграммы рассеивания.
Рассмотрим таблицу и выясним, есть ли связь между ростом и весом человека.

Для наглядного ответа построим диаграмму рассеивания. Данными этой диаграммы будут служить пары величин. Каждая пара – это рост и масса одного человека.

Чтобы построить диаграмму рассеивания, нужно в системе координат отметить данные точки. Абсциссы этих точек – рост юношей, а ординаты – соответствующая масса.
Сделаем это и получим диаграмму, точки которой образуют облако рассеивания.

Обратите внимание, что точки группируются вдоль некоторой наклонной прямой, направленной вправо и вверх. Это означает, что между величинами «рост» и «масса» имеется положительная связь, то есть чем выше человек, тем больше его масса. Разумеется, в каждом конкретном случае это правило может нарушаться. Например, в данной таблице есть юноша, рост которого равен 179 см, а масса – 70 кг, и юноша, рост которого равен 174 см, а масса – 73 кг. Но такая ситуация скорее является исключением.
Рассмотрим таблицу, в которой приведены данные о росте и массе 15 девушек.

Чтобы наглядно показать связь между ростом и весом девушек, можно построить диаграмму рассеивания, данными которой будут служить следующие 15 пар величин. Каждая пара – это рост и масса одной девушки.

Для построения диаграммы рассеивания, нужно в системе координат отметить эти 15 точек. Абсциссами точек является рост девушек, а ординатами – соответствующая масса.

Внимательно рассмотрев облако рассеивания, можно заметить, что между величинами «рост» и «масса» имеется положительная связь, то есть чем выше девушка, тем больше её масса. Конечно же, в некоторых случаях это правило нарушается.
Диаграмма рассеивания – это способ представления двух совместно наблюдаемых величин точками на координатной плоскости. Когда точек много, они образуют облако рассеивания.
По форме облака рассеивания можно составить наглядное представление об отсутствии или наличии связи между величинами и её характере. Чтобы лучше увидеть форму и наклон облака, можно обвести его фломастером или карандашом.
Пример. Мальчики на соревнованиях прыгали в длину с места и бежали 60 м. Их результаты приведены в таблице.

Построим диаграмму рассеивания, данными которой будут служить 14 пар величин. Каждая пара – это результат прыжка в длину и результат забега на 60 м.

Отметим в системе координат 14 точек, абсциссами которых является результат прыжка в длину, а ординатами – соответствующий результат забега на 60 м.
Обведём получившееся облако рассеивания зелёным цветом. Видим, что связь отрицательна – чем дальше школьник прыгает, тем меньше время забега. Хотя это правило тоже иногда нарушается.

Прежде чем приступить к рассмотрению следующего примера, отметим, что самочувствие человека во многом определяется температурой тела и артериальным давление.
Пример. Посмотрим на диаграмму рассеивания для температуры тела и артериального давления, построенную по данным обследования 25 человек, находящихся в больнице.

Облако рассеивание овальное. Оно вытянуто вдоль горизонтальной оси и практически не имеет наклона. В таком случае можно предположить, что связи между артериальным давлением и температурой тела нет. Так, например, у человека, заболевшего гриппом, может быть высокая температура, но при этом нормальное артериальное давление.
По форме облака рассеивания можно не только предположить наличие связи, но и оценить её силу.
Если облако не имеет явного наклона (то есть оно круглое или вытянутое по горизонтали или вертикали), то можно предположить, что связь между величинами отсутствует, то есть значения одной из них не влияет на значения другой.
Если облако имеет явный наклон, то важно, в какую сторону оно наклонено.
Если облако вытянуто вправо-вверх, то это говорит о том, что чем больше одна величина, тем больше вторая. В таком случае говорят, что между величинами наблюдается положительная связь.
Если облако вытянуто вправо-вниз, то это говорит о том, что чем больше первая величина, тем меньше вторая, и наоборот. В таком случае говорят, что между величинами наблюдается отрицательная связь.
Пример. Приведена таблица, в которой представлены данные о протяжённости и количестве станций линий Московского метрополитена по состоянию на сентябрь 2018 г.

Построим диаграмму рассеивания по этим данным. Обведём скопление точек зелёным цветом.

Получившееся облако имеет явный наклон вправо-вверх, то есть наблюдается положительная связь.
Сравним получившуюся диаграмму с диаграммой рассеивания, которую мы построили в первом примере. В обоих случаях величины положительно связаны, но в примере о метрополитене точки внутри облака расположены плотнее, поэтому овал сильнее вытянут. Можно предположить, что связь между длиной линии метро и количеством станций сильнее (теснее), чем связь между ростом и весом человека.
Посмотрите, как выглядят диаграммы с разной силой связи.

Иногда случается так, что связь есть, но на диаграмме её не видно. И наоборот – может показаться, что связь есть, но на самом деле её нет. Причины этого могут быть разными, но чаще всего так бывает, если данных мало. Чем больше имеется наблюдений, тем более обоснованным будет предположение.
Если облако на диаграмме имеет не овальную, а более сложную форму, то это означает, что связь между величинами тоже сложная.
Дана таблица, в которой приведены данные контрольных измерений изготовленных на заводе труб: диаметр и длина трубы массой 1 т.

Построив диаграмму рассеивания по этим данным, можно сделать вывод, что диаметр и длина трубы связаны. И эта связь отрицательна. При этом облако рассеивания в данном случае не овальное, а имеет изогнутую форму.

Посмотрите на рисунки, на которых схематично показано, как могут выглядеть диаграммы рассеивания при сложных связях: точки группируются не внутри овала, а внутри более сложной, часто невыпуклой фигуры.

Диаграмма рассеивания – не доказательство наличия или отсутствия связи между величинами. С помощью диаграммы можно лишь предположить, что связь есть или что её нет. При этом чем больше наблюдений, тем более обосновано предположение.
Наличие связи не означает, что одна величина обусловлена другой. Наблюдаемая связь далеко не всегда причинно-следственная. Механизм связи может быть сложным. Часто обе величины зависят не друг от друга, а от каких-либо ещё факторов, которые не входят в исследование.
Например, рассматривая связь между результатом прыжка в длину и результатом забега на 60 м, нельзя сказать, что школьник прыгает дальше потому, что быстрее бегает, и наоборот. Ведь общее физическое развитие, рост, тренированность обусловливают обе величины.
В завершение занятия следует сказать, что диаграммы рассеивания (или точечные диаграммы) являются одним из ключевых инструментов визуализации данных в статистике. Они позволяют наглядно исследовать взаимосвязь между двумя переменными, выявлять закономерности, тренда и аномалии в данных.
Диаграммы рассеивания широко применяются в различных областях: от экономики и маркетинга до медицины и инженерии. Они помогают не только увидеть общую картину распределения данных, но и сделать некоторые выводы о возможных зависимостях.
До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход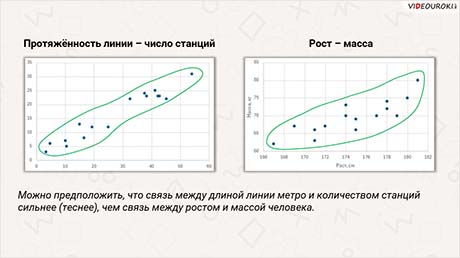




 1334
1334

