Напомним, что в массиве чисел отклонением числа от среднего арифметического, или просто отклонением, называется разность между этим числом и средним арифметическим набора.
Модуль отклонения называют абсолютным отклонением.
Среднее арифметическое квадратов отклонений чисел от их среднего арифметического называется дисперсией набора чисел.
Дисперсия – это средний квадрат отклонений.
Слово «дисперсия» в переводе с латинского языка означает «рассеивание, разброс».
Несмотря на то, что дисперсия – удобная мера рассеивания, у неё есть серьёзный недостаток, который затрудняет её практическое применение. Дело в единицах измерения.
Например, если дан массив расстояний в километрах, то среднее арифметическое, медиана и другие центральные меры тоже будут измеряться в километрах. А вот дисперсия будет измеряться в квадратных километрах, так как представляет собой многочлен второй степени.
Посмотрите на таблицу, в которой приведена средняя месячная температура за 80 лет в Москве, Пензе, Новосибирске и Хабаровске.

В последней строке этой таблицы найдена дисперсия. Обратите внимание, что в данном случае она измеряется в ºС². И это кажется нам необычным. Чтобы избавиться от этого недостатка, нужно извлечь из дисперсии квадратный корень.
Квадратный корень из дисперсии числового массива называется стандартным отклонением этого массива.
Формулу стандартного отклонения можно записать так

или так

Стандартное отклонение – это некоторое среднее отклонение чисел набора.
Важно отметить, что это среднее не является средним арифметическим. Квадратный корень из среднего квадрата называют средним квадратичным. Таким образом, стандартное отклонение – это среднее квадратичное отклонение от среднего арифметического.
Пример. Дан числовой набор  .
.

Подставим найденные значения в формулу для нахождения дисперсии  и выполним вычисления.
и выполним вычисления.

Тогда  .
.
Расположим числа набора на числовой прямой. На этой же прямой отметим среднее арифметическое. Отложим от него слева одно стандартное отклонение и справа.

Соединим отмеченные значения отрезком зелёного цвета и увидим, что некоторые точки оказались внутри отрезка, некоторые – снаружи, а одна точка даже оказалась концом этого отрезка.

В следующей таблице приведены данные о населении всех городов Московской области в 2019 году.

Обратите внимание, что численность населения таких городов, как Балашиха, Подольск и Верея, сильно отличается от численности населения большинства городов (Балашихи и Подольска – значительно больше, а Вереи – значительно меньше).
Удалив два очень больших и одно очень маленькое значение из данной таблицы, найдём среднее и стандартное отклонение.

Если отступить от среднего на одно отклонение влево и на одно
отклонение вправо, то получится отрезок  .
.
Если население города попадает в этот отрезок, то такой город можно считать типичным по численности населения. Города, численность которых меньше 10,5 тыс. чел., можно считать малыми, а города, численность которых больше 124,9 тыс. чел., можно считать крупными.
Таким образом, выбрано решающее правило, которое позволяет определить, что такое малый и что такое крупный подмосковный город.
Решающие правила можно выбирать разными способами. Например, можно опираться на полтора, два или три стандартных отклонения. Конечно же, существуют и другие способы.
Чтобы найти стандартное отклонение в электронной таблице, можно извлечь корень из дисперсии (КОРЕНЬ(ДИСПР())). Но в современных редакторах есть специальная функция СТАНДОТКЛОН.Г().

Стандартное отклонение играет большую роль в массовом производстве. Значительный износ оборудования приводит к большому рассеиванию параметров готовой продукции. Следовательно, измерение рассеивания во время контроля качества продукции позволяет косвенно судить о состоянии оборудования.
Пример. Рассмотрим таблицу, в которой приведены результаты контрольного взвешивания двух партий булок, испечённых на хлебозаводе на двух одинаковых производственных линиях. Номинальная масса булки 200 г. Масса готовой булки зависит от количества теста, которое отмерил дозирующий автомат.

В первой партии среднее отклонение от номинального значения равно
6,1 г (200 –193,9 = 6,1), во второй партии – 1,4 г (200 – 198,6 = 1,4).
Можно подумать, что первая линия работает лучше. Но давайте посмотрим на стандартное отклонение. В партии продукции, взятой со второй линии, оно равно 4,18 г, а в партии продукции, взятой с первой линии, оно равно только 1,3 г. Это означает, что первая линия требует лишь небольшой регулировки для того, чтобы дозатор отмерял примерно на 6 – 7 г теста больше, чем сейчас. А вот вторая линия изношена. Возможно ей даже нужен ремонт.
При производстве массовой продукции высокое рассеивание параметров готовой продукции (массы, размеров и тому подобного) может говорить о большом износе оборудования и необходимости ремонта.
Смещение средних значений параметров при низком рассеивании, как правило, устанавливается регулировкой.
Выполним задания.
Задание первое. Найдите стандартное отклонение числового массива, если его дисперсия равна:

Решение. Стандартным отклонением числового массива называется квадратный корень из дисперсии этого массива.

Задание второе. Найдите стандартное отклонение числового набора 3, 5, 7, 3, 6, 4, 3, 1, 0, 6. Результат округлите до сотых.
Решение.

Задание третье. Дан набор из пяти чисел: 1, 5, 6, 3, 2. Найдите стандартное отклонение. Результат округлите до сотых. Найдите отрезок, который получается, если отступить от среднего арифметического значения влево и вправо на одно стандартное отклонение. Какие значения попадают в этот отрезок? Какие значения расположены левее левой границы этого отрезка? Какие значения расположены правее правой границы?
Решение.

До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход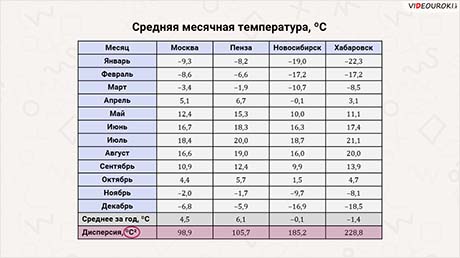




 2088
2088

