Поговорим о специальных графах – деревьях. Но сначала давайте напомним, что граф – это изображение объектов и связей между ними с помощью точек и линий. Точки в графе называются вершинами графа. Вершины (не обязательно все) соединены линиями, которые называются рёбрами графа.
Если вершина является концом ребра, то говорят, что ребро исходит из этой вершины или что оно входит в неё. При этом вершина не обязательно должна быть соединена рёбрами с другими вершинами.
Вершину, из которой не выходит ни одно ребро, называют изолированной.

Обратите внимание, что рёбра графа могут пересекаться, но точка их пересечения не является вершиной графа. Это как две нитки: одна пересекает другую, но узелка в точке пересечения нет.
Также напомним, что степенью вершины графа называют количество рёбер, исходящих из этой вершины. Иногда степень вершины называют валентностью вершины.
Вершина называется чётной, если из неё выходит чётное число рёбер, и нечётной, если из неё выходит нечётное число рёбер.
Иногда приходится рассматривать граф с петлёй, то есть с ребром, которое исходит из вершины и входит в неё же. При подсчёте степени вершины такое ребро считается дважды.
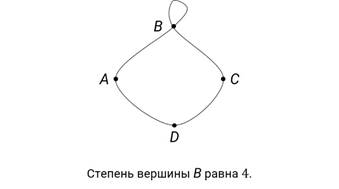
В теореме о сумме степеней вершин графа говорится, что в любом графе сумма степеней всех вершин является чётным числом. И это действительно так, ведь у каждого ребра два конца, а значит, сумма степеней всех вершин в два раза больше числа рёбер, то есть чётное число.
В любом графе количество вершин нечётной степени чётно.
А теперь давайте напомним, что такое цепь и цикл в графе.
Цепь (простой путь) – это путь в графе из одной вершины в другую, в котором вершины и рёбра не повторяются.
Если граф состоит из одной-единственной цепи, то такой граф также называют цепью. Граф без рёбер, состоящий из единственной вершины, считают цепью.
Цикл в графе – это замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются.
Простейший цикл представляет собой петлю, которая состоит из одной вершины и одного ребра.
Если граф состоит из одного цикла, то такой граф также называют циклом.
Особый интерес вызывают графы, в которых нет циклов.
Если в связном графе нет циклов, то такой граф называют деревом.
Напомним, что граф называется связным, если две любые вершины в этом графе соединены путём.

Дерево – это связный граф без циклов.
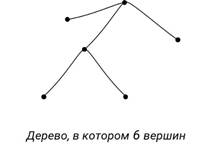
Цепь тоже является деревом, поскольку в цепи нет циклов. И даже граф, который состоит из одной-единственной вершины без рёбер, можно рассматривать как простейшее дерево.

Посмотрите на схему водоснабжения в небольшом населённом пункте. Обратите внимание, что трубы идут от водонапорной башни и ветвятся, пролегая вдоль улиц. От больших труб к домам отходят малые трубы.
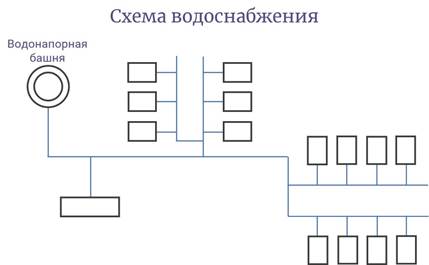
Эта схема представляет собой связный граф без циклов, то есть дерево. В этом графе можно выделить начальную вершину – водопроводную башню, так как по трубам вода течёт именно оттуда.
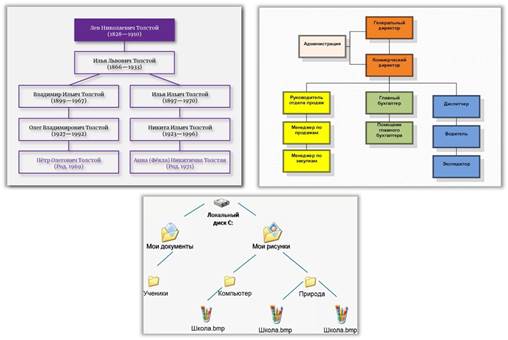
Также примером связного графа без цикла является родословное дерево, модель организационной структуры небольшой фирмы, файловая структура диска компьютера.
Теперь рассмотрим пример с подбрасыванием математической монеты.
Напомним, что математическая монета, которая используется в теории вероятностей, лишена многих качеств настоящей монеты. У неё нет цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платёжным средством.
С точки зрения теории вероятностей математическая монета имеет две стороны, одна из которых называется орлом, а другая – решкой.
Математическая монета считается симметричной. Это означает, что брошенная монета имеет равные шансы выпадения орла или решки. При этом подразумевается, что никакой другой исход бросания монеты невозможен.
Подбрасывание монеты – случайный эксперимент, который может окончится либо выпадением орла, либо выпадением решки. Всего два события, одно из которых обязательно произойдёт.
Давайте возьмём симметричную монету и подбросим её 3 раза. Чтобы изобразить этот случайный эксперимент, мы с вами построим дерево.
Начальную вершину обозначим буквой S От неё проведём вниз 2 ветви к вершинам, которые обозначим буквами О и Р. Это означает, что в результате первого броска выпал орёл или решка. Затем от каждой из этих вершин проведём ещё по 2 ребра к вершинам О и Р, которые изображают результаты второго броска. Далее точно так же покажем результаты третьего броска.
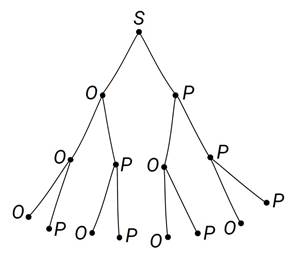
Таким образом, получилось дерево случайного эксперимента. В этом дереве 8 цепей, ведущих из начальной вершины S в концевые вершины. Каждая цепь изображает 1 из 8 возможных элементарных событий в случайном эксперименте с подбрасыванием симметричной монеты три раза.
Следует отметить, что в этом примере начальная (или корневая) вершина S изображает начальный момент, то есть момент, когда монету ещё ни разу не бросили. S – это начало случайного эксперимента.
Название «дерево» означает, что цепи «ветвятся», не образуя циклов. Вот только в природе деревья растут снизу вверх, а математические деревья мы рисуем так, как нам удобно.
Бывают бесконечные деревья, то есть деревья, в которых бесконечно много вершин и рёбер.
Давайте представим, что грибник пытается отправить СМС из леса, где очень плохая связь. Каждая попытка может оказаться как удачной, так и неудачной. В случае неудачной попытки телефон предпринимает следующую. Будем считать, что попыток может быть бесконечно много.
Такой случайный эксперимент можно изобразить с помощью бесконечного графа. Пусть такой граф начинается в вершине S. Каждая попытка отправить СМС может оказаться удачной или неудачной.
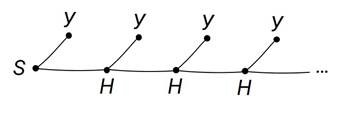
Обратите внимание на многоточие. Оно показывает, что дерево простирается вправо до бесконечности.
Выполним несколько заданий.
Задание первое. Рассмотрите графы, изображённые на рисунках. Какие из них являются деревьями?
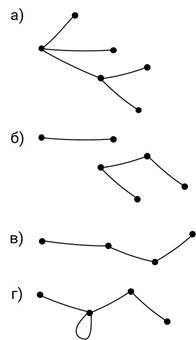
Решение.
Посмотрим на граф, который показан на рисунке а). Видим, что это связный граф без циклов, а значит, он является деревом.
Граф, изображённый на рисунке б) не является деревом, так как он несвязный.
Граф на рисунке в) представляет собой цепь. Поскольку у цепи нет циклов, этот граф является деревом.
На рисунке г) изображён граф с петлёй. Петля, которая состоит из одной вершины и одного ребра, является простейшим циклом. Так как дерево – это связный граф без циклов, то данный граф деревом не является.
Получается, что только два графа из четырёх являются деревьями.
Задание второе. План дорожек в зоопарке представляет собой дерево. Ворота зоопарка обозначены вершиной S. Сколько цепей ведут из вершины S к тигру, ко льву, к леопарду?

Решение.
К тигру ведут 3 цепи. Ко льву ведут две цепи. К леопарду ведёт только одна цепь.
До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход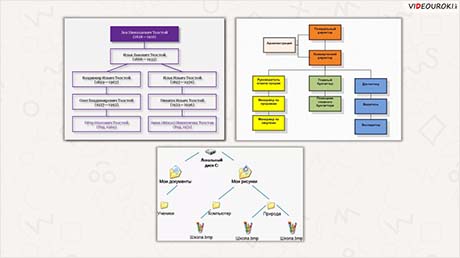




 1343
1343

