Свойства деревьев

Прежде чем приступить к рассмотрению новой темы, напомним, что дерево – это связный граф без циклов. Также деревом является цепь, поскольку в ней нет циклов. Граф, который состоит из одной-единственной вершины без рёбер, тоже можно рассматривать как простейшее дерево. Деревья бывают бесконечными. У таких деревьев бесконечно много вершин и рёбер.

Название «дерево» означает, что цепи «ветвятся», не образуя циклов. Только вот в природе деревья растут снизу вверх, а математические деревья мы рисуем так, как нам удобно.

Давайте поговорим о свойствах деревьев. Итак, поскольку дерево – связный граф, то из любой его вершины можно пройти по рёбрам в любую другую вершину. Так как дерево – это связный граф без циклов, то это можно сделать единственным способом. Следовательно, верна следующая теорема.

Теорема. Любые две вершины в дереве соединены единственной цепью.

Из этой теоремы следует важное свойство.

Свойство 1. Если из дерева удалить ребро, то граф перестанет быть связным.

Докажем это свойство методом от противного.

Предположим, что нам удалось удалить некоторое ребро АВ так, что граф остался связным. А значит, в нём есть цепь, которая соединяет вершины А и В.

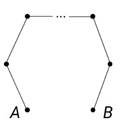
Вернув ребро АВ на место, получим исходный граф. Но теперь в нём есть цикл.

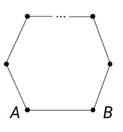
Получили противоречие. Следовательно, при удалении любого ребра дерево теряет связность.

Свойство доказано.

Определение. Концевой (висячей) вершиной называется вершина графа, из которой выходит ровно одно ребро, то есть вершина степени один.

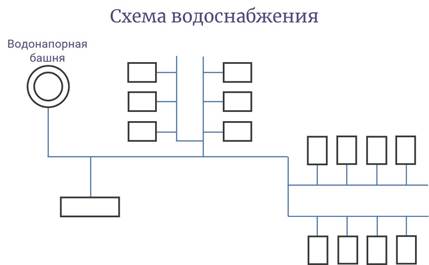
Например, в схеме водоснабжения в небольшом населённом пункте концевыми вершинами являются дома, к которым подведён водопровод.

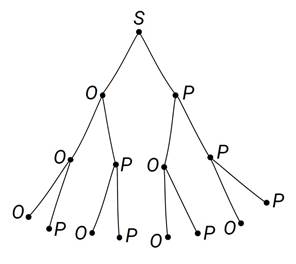
У дерева случайного эксперимента с подбрасыванием симметричной монеты концевыми вершинами являются результаты последнего броска монеты.

Можно подумать, что раз в дереве нет циклов, то у него обязательно должны быть концевые вершины. И это в некоторой степени верно. Но есть два исключения.

1. Концевых вершин нет у дерева без рёбер.

2. Бывают бесконечные деревья. Они тоже могут не иметь концевых вершин.

Посмотрите на бесконечное дерево без концевых вершин.

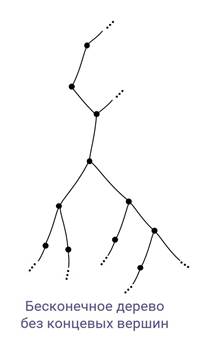
Но не нужно думать, что если дерево бесконечно, то у него обязательно нет концевых вершин. Например, у бесконечного дерева, которое изображает случайный эксперимент с попытками грибника отправить СМС из леса, где очень плохая связь, концевые вершины есть. И даже бесконечно много.

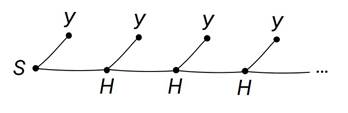
Если дерево конечно и имеет хотя бы одно ребро, то концевые вершины у него есть.

Свойство 2. Если в дереве конечное число вершин и есть хотя бы одно ребро, то в таком дереве есть концевая вершина.

Докажем это свойство методом от противного.

Предположим, что все вершины имеют степень 2 и выше. Тогда в каждую вершину можно «войти» по какому-то ребру и «выйти» из неё по другому ребру, так как петель нет.

Начнём с некоторой вершины и будем строить путь без повторяющихся рёбер. В условии сказано, что вершин конечное число, а значит, рано или поздно какая-то вершина в нашем пути повторится. Получится цикл. Но ведь в дереве нет циклов.

Получили противоречие. Значит, предположение неверно. Следовательно, в дереве есть вершины степени меньше, чем 2. Но вот вершин степени 0 нет, поскольку граф связен и в нём есть хотя бы одно ребро.

Получается, что найдётся вершина степени 1, то есть концевая вершина.

Свойство доказано.

Свойство 3. В конечном дереве число рёбер на одно меньше числа вершин.

Доказательство.

Если рёбер нет, то дерево состоит из единственной вершины. Значит, в этом дереве вершин на одну больше, чем рёбер.

Теперь пусть в графе n рёбер (n > 0). В таком дереве есть концевая вершина. Давайте удалим её вместе с входящим в неё ребром. Снова получится дерево.

Продолжим удалять концевые вершины вместе с входящими в них рёбрами до тех пор, пока не останется дерево, состоящее из единственной вершины.

Итак, удалены n вершин и все n рёбер. Осталась одна вершина, но рёбер больше нет. Следовательно, в исходном дереве было n + 1 вершин. То есть вершин было на одну больше, чем рёбер.

Свойство доказано.

Выполним несколько заданий.

Задание первое. Сколько концевых вершин в деревьях, изображённых на рисунках?

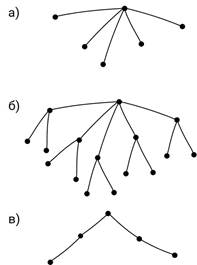
Решение.

Напомним, что концевой вершиной называется вершина графа, из которой выходит ровно одно ребро, то есть вершина степени 1.

В дереве на рисунке а) 5 концевых вершин.

В дереве на рисунке б) 10 концевых вершин.

В дереве на рисунке в) 2 концевых вершины.

Задание второе. В дереве 4 вершины. Сколько концевых вершин в нём может быть? Приведите пример дерева для каждого возможного значения.

Решение.

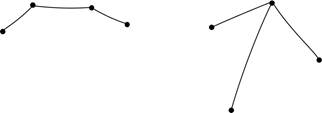
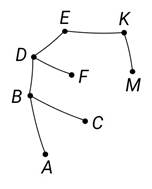
Задание третье. Изобразите дерево, в котором 7 вершин, причём концевыми являются ровно: а) 2 вершины; б) 4 вершины; в) 6 вершин.

Решение.

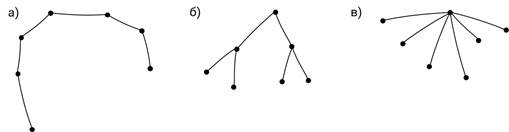
Задание четвёртое. Рассмотрите дерево, изображённое на рисунке. Сколько цепей, соединяющих начальную вершину S с концевыми, имеют: а) длину 2; б) длину 3; в) длину 4?

Решение.

Под длиной цепи понимают количество рёбер в этой цепи.

а) 2 цепи; б) 4 цепи; в) 1 цепь.

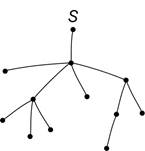
Прежде чем приступить к выполнению следующего задания, отметим, что количество рёбер в максимальной цепи, то есть цепи, связывающей две наиболее удалённые вершины, называют диаметром дерева.

Например, в данном дереве наиболее удалёнными являются вершины А и М. Количество рёбер между ними равно 5. А значит, диаметр этого дерева равен 5.

Задание пятое. Сколько вершин в дереве, в котором: а) 12 рёбер; б) 39 рёбер?

Решение.

Чтобы ответить на этот вопрос, напомним, что в конечном дереве число рёбер на одно меньше числа вершин.

Тогда получается, что в дереве, в котором 12 рёбер, будет 13 вершин. А в дереве, в котором 39 рёбер, будет 40 вершин.

До встречи на следующих занятиях!