Прежде чем приступить к рассмотрению новой темы, напомним, что дерево – это связный граф без циклов. Цепь тоже является деревом, поскольку в цепи нет циклов. И даже граф, состоящий из одной-единственной вершины без рёбер, также можно рассматривать как простейшее дерево.
Перед вами дерево случайного эксперимента, в котором симметричную монету подбрасывают 3 раза.

В этом дереве 8 цепей, ведущих из начальной вершины S в концевые вершины. Каждая цепь изображает 1 из 8 возможных элементарных событий в этом случайном эксперименте.
В данном примере корневая вершина S изображает начальный момент, то есть момент, когда монету ещё ни разу не бросили. Можно сказать, что S – это начало случайного эксперимента.
Деревья бывают бесконечными. У таких деревьев бесконечно много вершин и рёбер.
Посмотрите на дерево случайного эксперимента, в котором грибник пытается отправить СМС из леса, где очень плохая связь. Каждая попытка может оказаться как удачной, так и неудачной. В случае неудачной попытки телефон предпринимает следующую. Многоточие показывает, что дерево простирается вправо до бесконечности, так как попыток может быть бесконечно много.

Многие случайные эксперименты удобно рассматривать, изобразив их с помощью дерева. При этом стрелки на рёбрах можно не рисовать, ведь всегда понятно, какая вершина выбрана в качестве начальной, так как все ребра направлены от неё к концевым вершинам. Начальную вершину дерева случайного эксперимента обычно обозначают буквой S.
Пример. На фабрике керамической посуды производят тарелки. Каждая новая тарелка может иметь дефект, а может оказаться качественной. Все тарелки проходят контроль качества. Система контроля качества выявляет почти все дефектные тарелки, но иногда может случайно не заметить дефект. Редко, но случается, что система контроля по ошибке бракует тарелку без дефекта.
Изобразим этот процесс с помощью дерева.
Обозначим начальную вершину буквой S. От неё проведём вниз ребро к вершине К, которая изображает событие «качественная тарелка» и ребро к вершине Д, которая изображает событие «дефектная тарелка». Затем от вершины К проведём ребро к вершине Б, изображающей событие «тарелка забракована» и ребро к вершине Н, изображающей событие «тарелка на забракована». Также от вершины Д проведём ребра к вершинам Б и Н.

Обратите внимание, что вершины Б и Н нарисованы 2 раза: один раз для случая, когда тарелка качественная, а второй раз для случая, когда тарелка дефектная.
Получившееся дерево обладает интересным свойством: у него из каждой неконцевой вершины (то есть из вершин S, К и Д) исходит ровно 2 ребра. Такие деревья называют двоичными, или бинарными.
Снова посмотрите на дерево случайного эксперимента, в котором симметричную монету подбрасывают 3 раза, и на дерево случайного эксперимента, в котором грибник пытается отправить СМС из леса, где очень плохая связь. Эти деревья тоже можно назвать бинарными.
Какие события в этом опыте являются элементарными?
Это события, которые изображены цепями, идущими от начальной точки S к концевым вершинам. Получается, что в данном эксперименте всего 4 элементарных события.
Не следует думать, что дерево любого случайного эксперимента обязательно бинарное.
Пример. Катя, Лена и Оля в случайном порядке встают в очередь. Изобразим дерево этого случайного эксперимента.
Обозначим начальную вершину дерева буквой S. На первое место в очереди можно поставить Катю, Лену или Олю.
Если Катя встала в очередь первой, то на второе место можно поставить Лену или Олю.
Если Лена встала в очередь первой, то на второе место можно поставить Катю или Олю.
Если же в очередь первой встала Оля, то на второе место можно поставить Катю или Лену.
Теперь определим, кто будет стоять в конце очереди.
Если первой в очередь встала Катя, а за ней Лена, то последней в очереди будет Оля.
Если после Кати в очередь встала Оля, то последней в очереди будет Лена.
Если первой в очередь встала Лена, а за ней Катя, то последней в очереди будет Оля.
Если после Лены в очередь встала Оля, то последней в очереди будет Катя.
Если первой в очередь встала Оля, а за ней Катя, то последней в очереди будет Лена.
Если же после Оли в очередь встала Лена, то последней в очереди будет Катя.

Получилось дерево, у которого из вершины S выходит 3 ребра. Из трёх вершин выходит по 2 ребра. А из 6 вершин выходит только по 1 ребру. Следовательно, это дерево не бинарное.
В данном случайном эксперименте 6 элементарных событий. В дереве все эти элементарные события изображены цепями, ведущими от начальной вершины S к концевым вершинам дерева. Каждая из цепей определяет порядок, в котором Катя, Лена и Оля выстроились в очередь.

В дереве случайного эксперимента элементарные события изображаются цепями, идущими от начальной вершины к концевым. Поэтому количество концевых вершин в дереве случайного эксперимента равно числу элементарных событий.
Выполним несколько заданий.
Задание первое. На рисунке изображено дерево некоторого случайного эксперимента с началом в точке S. Сколько элементарных событий в этом эксперименте?

Решение.
Чтобы ответить на этот вопрос, напомним, что количество концевых вершин в дереве случайного эксперимента равно числу элементарных событий.
В дереве 10 концевых вершин, а значит, элементарных событий в рассматриваемом случайном эксперименте тоже 10.
Задание второе. На рисунке изображено дерево некоторого случайного эксперимента с началом в точке S. Сколько элементарных событий в этом эксперименте благоприятствуют событию А, событию В?

В дереве случайного эксперимента элементарные события изображаются цепями, идущими от начальной вершины к концевым. Количество концевых вершин в дереве случайного эксперимента равно числу элементарных событий.
Тогда чтобы выяснить, сколько элементарных событий в эксперименте благоприятствует событию А, надо сосчитать концевые вершины цепей, проходящих через вершину А.
Получается, что событию А благоприятствуют 7 элементарных событий.
Чтобы выяснить, сколько элементарных событий благоприятствуют события В, надо сосчитать концевые вершины цепей, проходящих через вершину В.
Получается, что событию В благоприятствуют 5 элементарных событий.
Задание третье. На рисунке изображено дерево случайного эксперимента, в котором симметричную монету бросают 3 раза. Отметьте в этом дереве цепочки, изображающие элементарные события, которые благоприятствуют данным событиям.


Первое событие «во второй раз выпала решка». Этому событию благоприятствуют 4 элементарных события.
Второе событие «орёл выпал ровно два раза». Этому событию благоприятствуют 3 элементарных события.
Третье событие «решек выпало больше, чем орлов». Этому событию благоприятствуют 4 элементарных события.
До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход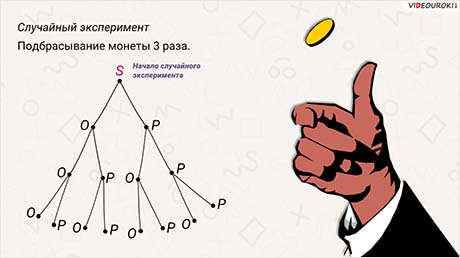




 1486
1486


