Давайте представим себе такую историю.
– Саша, чем ты занимаешься? – поинтересовался у друга Паша.
– Папа научил меня делать самолётик оригами! – восхищался Саша. – Посмотри, как круто летает такой самолётик!

– Да… его полёт завораживает! – наблюдал за самолётиком Паша. – Только вот я бы уточнил, что искусство создания бумажных самолётиков называется аэрогами или бумажная авиация. Это одна из техник оригами, при которой необходимо не только сложить красивую фигурку, похожую на оригинал, но и предусмотреть её лётные характеристики. Самолёты из бумаги были известны более 2000 лет назад. Однако тогда это были не самолётики, а птички.

Датой создания бумажного самолётика считается 1909 год, но более популярной датой является 1930 год. Тогда основатель известной компании по аэродинамике Lockheed Corporation Джек Нортроп заинтересовался, как из бумаги сделать самолёт.
– А зачем этому человеку нужны были бумажные самолётики? – поинтересовался Паша.
– Изобретатель хотел протестировать на бумажных самолётах свои новые идеи, – продолжил Паша. – Использование бумажной подделки в воздухе помогало правильно подбирать форму для будущих летательных аппаратов.
– Как же это интересно! – с восторгом сказал Саша.
– И это ещё не всё! – продолжил Паша. – В наши дни бумажная авиация, или аэрогами, получила мировую известность. Каждый человек знает, как сложить элементарный самолётик и запустить его. Но на сегодняшний день это уже не просто забава, а серьёзное увлечение, по которому проводят соревнования по всему миру.

– Вот бы мне побывать на таких соревнованиях, – сказал Саша.
– Обязательно побываешь! – подбодрил друга Паша. – Главное верить в свою мечту! Ну и, конечно же, тебе ещё будет полезным познакомиться с условиями создания и схемами бумажных самолётиков. Одними из главных условий создания самолётика являются использование бумаги прямоугольной или квадратной формы и чёткое соблюдение симметрии.
– Ого! – задумался Саша. – Вот про прямоугольные и квадратные формы я всё знаю, а про симметрию совсем ничего, – расстроился он.
– А давай спросим у Электроши, – предложил Паша. – Он точно всё знает!
– Ребята, прежде чем я вам расскажу о прямоугольниках и симметрии, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь поговорим о прямоугольниках, – предложил Электроша. – И сразу начнём с вопроса: как вы понимаете, что такое прямоугольник?
– Прямоугольник – это четырёхугольник, у которого все углы прямые, – ответил Паша.
– Молодец! – похвалил Пашу Электроша. – Посмотрите: на листе изображён прямоугольник ABCD. Вы уже знакомы с элементами многоугольников. Назовите элементы нашего прямоугольника.
– Прямоугольник ABCD имеет 4 вершины: А, B, C и D, 4 одноимённых угла и 4 стороны: AB, BC, CD и DA – ответил Саша.
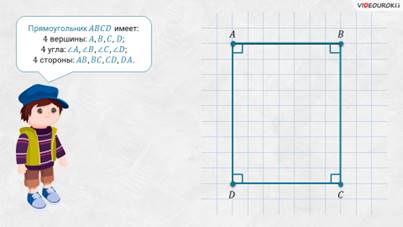
– Всё верно! – подтвердил Электроша. – Посмотрите: стороны AB и BC имеют общую вершину B. Такие стороны называют соседними сторонами прямоугольника ABCD. Также соседними сторонами будут стороны BC и CD с общей вершиной C, CD и DA с общей вершиной D, DA и AB с общей вершиной А.
Соседние стороны прямоугольника являются его измерениями, и их называют длиной и шириной.
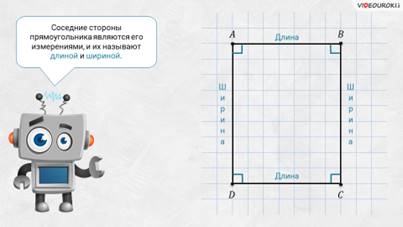
– А что вы можете сказать о сторонах, например, AB и CD нашего прямоугольника ABCD? – спросил у ребят Электроша.
– Стороны AB и CD не имеют общих вершин, – ответили мальчишки.
– Молодцы! – похвалил ребят Электроша. – Такие стороны называют противолежащими сторонами прямоугольника ABCD. Также противолежащими будут стороны BC и AD. Запомните! Противолежащие стороны прямоугольника равны.

– А теперь посмотрите: на листке изображён прямоугольник ABCD, его противолежащие стороны равны. Если длину прямоугольника обозначить буквой а, а ширину – буквой b, то его периметр можно вычислить по формуле: P = 2a + 2b.
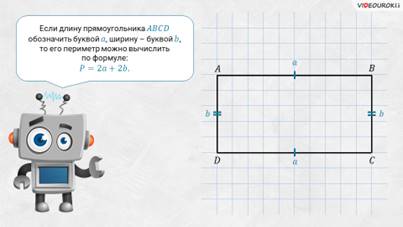
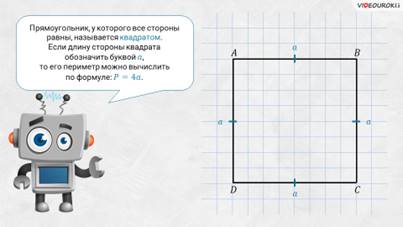
– Среди прямоугольников есть особые, – продолжил Электроша, – у которых все стороны имеют одну и ту же длину. Вы, конечно, помните, что такие прямоугольники называют квадратами. Если длину стороны квадрата обозначить буквой а, то его периметр можно вычислить по формуле: P = 4a.
– А теперь давайте проведём небольшой эксперимент. Возьмите лист бумаги прямоугольной формы и сложите его пополам так, чтобы противолежащие стороны совпали. Затем разверните этот лист. Что вы можете сказать о двух частях, получившихся в результате сгиба листа? – спросил у ребят Электроша.
– Видно, что две части нашего прямоугольного листа, лежащие по разные стороны от линии сгиба, совпадают.
– Молодцы! – похвалил ребят Электроша. – Прямую, которую мы получили в результате сгибания листа, называют осью симметрии.

Запомните! Ось симметрии – это прямая (или воображаемая линия), которая делит геометрическую фигуру на две зеркально одинаковые фигуры. Фигуру, которая имеет ось симметрии, называют симметричной относительно прямой.

– Скажите, сколько осей симметрии имеет прямоугольник? – спросил Электроша.
– Так как у прямоугольника 2 пары противолежащих сторон, то через их середины можно провести 2 оси симметрии, – сказал Паша.
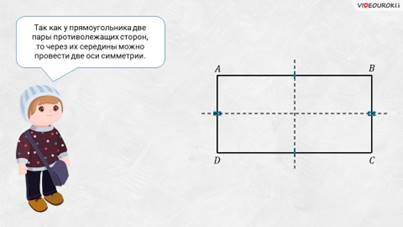
– Правильно! А, может, вы ещё сможете привести примеры симметричных фигур в геометрии?
– Например, квадрат, – начал Саша. – У квадрата тоже 2 пары противолежащих сторон, значит, через их середины можно провести 2 оси симметрии.
– Саша, ты чуть-чуть не досчитался! – сказал Электроша. – Вы уже знакомы с таким понятием, как диагональ. Напомню, что диагональ – это отрезок, соединяющий любые две несоседние вершины.
Если лист квадратной формы сложить пополам по диагоналям, то заметим, что и эти пары частей совпадут относительно линий сгиба.
– Значит, у квадрата 4 оси симметрии? – уточнил Саша.
– Верно! – ответил Электроша – Квадрат имеет 4 оси симметрии: 2 оси симметрии проходят через середины противолежащих сторон и 2 – через диагонали квадрата.
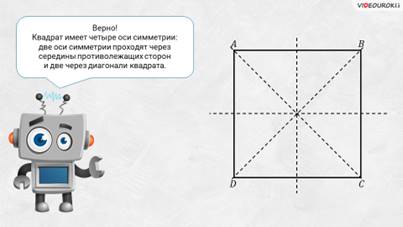
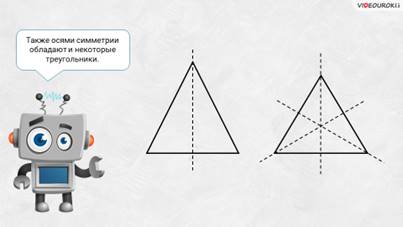
Также осями симметрии обладают и некоторые треугольники. Так, например, в равнобедренном треугольнике можно провести 1 ось симметрии, а в равностороннем – 3.
– С симметрией вы очень часто встречаетесь и в жизни. Люди с давних времён используют симметрию в рисунках, орнаментах, предметах быта, архитектуре, искусстве.

Даже многие буквы нашего алфавита обладают симметрией.

Однако больше всего восхищает симметрия в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, окраске и расположении различных органов животных, в форме кристаллических тел.
В порхающей бабочке и сказочной зимней снежинке.
Объекты, которые обладают осью симметрии, всегда легко воспринимаются и приятны для глаза. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». Симметрия означает соразмерность, наличие определённого порядка в расположении частей.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
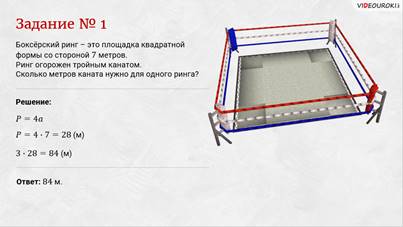
Задание первое: боксёрский ринг – это площадка квадратной формы со стороной 7 м. Ринг огорожен тройным канатом. Сколько метров каната нужно для одного ринга?
Решение: чтобы узнать, сколько понадобится метров каната для ринга, нужно знать периметр ринга. Мы знаем, что ринг имеет форму квадрата со стороной 7 м. Применяя формулу для вычисления периметра квадрата, получаем, что наш ринг имеет периметр 28 м. Так как ринг огорожен тройным канатом, то для одного ринга понадобится 84 метра каната.
Следующее задание: сколько осей симметрии имеет шестиугольник с равными сторонами?
Решение: так как, по условию, шестиугольник имеет равные стороны, а их 6, значит, можно провести 3 оси симметрии через середины противолежащих сторон. Также можно провести ещё 3 оси симметрии через диагонали шестиугольника. Тогда всего получим 6 осей симметрии.

Ось симметрии – это прямая (или воображаемая линия), которая делит геометрическую фигуру на две зеркально одинаковые фигуры.
Фигуру, которая имеет ось симметрии, называют симметричной относительно прямой.
У прямоугольника 2 оси симметрии, у квадрата – 4, у равнобедренного треугольника – 1, а у равностороннего – 3.

 Получите свидетельство
Получите свидетельство Вход
Вход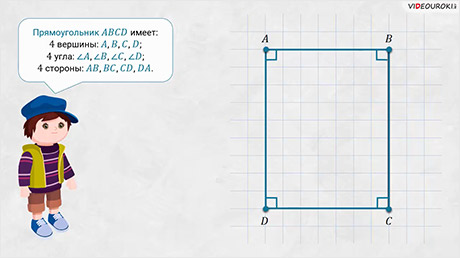



 0
0 12026
12026

