Умножение. Переместительное свойство умножения

Представим себе такую историю…

– И сколько же мне нужно купить конфет? – бормотал Саша.

– Что случилось? – поинтересовался Паша у друга.

– У нас в классе есть традиция. На свой день рождения мы приносим угощения для одноклассников. И мама дала мне задание купить конфеты.

– Ну и что тут сложного? – удивился Паша. – Идёшь в магазин и покупаешь конфеты.

– Да у нас в классе 16 учеников. А я хочу купить каждому по 3 конфеты. Тогда сколько конфет мне нужно купить?

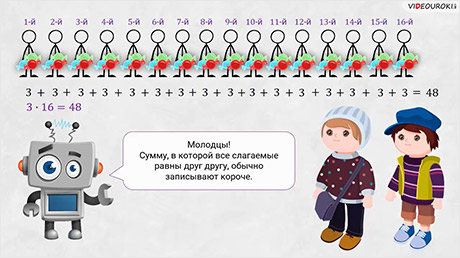
– Ну давай посчитаем вместе, – предложил Паша. – Итак, первому ученику – 3 конфеты, второму – 3, третьему – 3, четвёртому – 3, пятому – 3, шестому – 3, седьмому – 3, восьмому – 3, девятому – 3, десятому – 3, одиннадцатому – 3, двенадцатому – 3, тринадцатому – 3, четырнадцатому – 3, пятнадцатому – 3 и шестнадцатому – 3. Теперь сложим все конфеты и получим, что тебе нужно купить 48 конфет.

– Спасибо, Паша! – обрадовался Саша. – Но это так долго и нудно считать. А если бы у меня в классе было, например, 30 учеников, мы бы, наверное, целый день считали конфеты. Интересно, а существует ли какой-нибудь другой, более быстрый способ?

– А давай спросим у Электроши, – предложил Паша, – он точно будет знать такой способ.

 – Ребята, прежде чем я вам расскажу, как быстро решать подобные задачки, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь вернёмся к вашему вопросу, – предложил Электроша. – Чтобы посчитать, сколько конфет нужно купить Саше в школу, вы составили вот такую длинную запись.

Согласитесь, она не очень удобна, да и пока посчитаешь, можно 300 раз ошибиться. Но что особенного можно заметить в этой записи? – спросил у ребят Электроша.

– Эта запись представляет собой сумму чисел, все слагаемые которой одинаковые, то есть каждое слагаемое равно 3, – заметили мальчишки.

– Молодцы! – похвалил ребят Электроша. – Так вот, сумму, в которой все слагаемые равны друг другу, обычно записывают короче. Вместо вашей длиннющей записи пишут просто .

Запомните! Действие нахождения суммы одинаковых слагаемых называется умножением.

В нашем равенстве натуральные числа 3 и 16 называют множителями, число 48 и саму запись   – произведением.

Если в нашем равенстве числа 3, 16 и 48 заменить на натуральные числа а, b и c соответственно, то числа а и b называют множителями, а число c и саму запись – произведением.

Произведением числа а на натуральное число b, не равное одному, называют сумму, состоящую из b слагаемых, каждое из которых равно а.

В буквенном виде записывают так: .

– Электроша, а что будет, если b = 1? – решил уточнить Паша.

– Тогда придётся рассматривать сумму, которая состоит всего лишь из одного слагаемого, – начал Электроша.

– А разве в математике такое бывает? – перебил Паша.

– В математике сумму из одного слагаемого не принято находить, – сказал Электроша, – поэтому договорились, что .

– А если бы b = 0? – спросил Саша. – Тогда нужно было бы число а умножить на 0? То есть взять это число слагаемым 0 раз? Но ведь 0 – это нисколько! Сколько же тогда получится?

– Если b = 0, – начал Электроша, – то договорились считать, что . Точно так же получится и если .

– А если, наоборот, 1 и 0 нужно умножить на некоторое натуральное число а? – решили уточнить ребята.

– Давайте рассмотрим произведения и , где а – натуральное число, отличное от единицы, – предложил Электроша.

– Смотрите,   будет равно сумме единиц, которая состоит из а слагаемых. Чему будет равна такая сумма?

– Такая сумма будет равна а.

– Молодцы! – похвалил ребят Электроша.

– А значит,   будет равно сумме нулей, состоящей из а слагаемых и равно 0, – предположили ребята.

– Всё верно! – сказал Электроша. – Можем сделать следующие выводы. Запомните! Если один из двух множителей равен единице, то произведение равно другому множителю.

Если один из множителей равен нулю, то произведение равно нулю.

Произведение двух чисел, отличных от нуля, нулём быть не может.

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

– А теперь давайте проведём небольшой эксперимент, – предложил Электроша. – Начертите на листке в клетку прямоугольник со сторонами 5 см и 3 см. Затем разделите этот прямоугольник на квадраты со стороной 1 см. Скажите, как подсчитать количество получившихся квадратов?

– Так как прямоугольник разделён на 3 ряда и каждый ряд состоит из 5 квадратов, – начал рассуждать Саша, – то можно 5 умножить на 3. Получим, что прямоугольник состоит из 15 квадратов.

– Но ведь можно смотреть и с другой стороны, – перебил друга Паша. – Прямоугольник разделён на 5 столбцов. Каждый столбец состоит из 3 квадратов. Значит, количество квадратов можно посчитать как 3 умножить на 5. Тоже получим, что прямоугольник состоит из 15 квадратов.

– Вы оба правильно рассуждаете, – сказал Электроша. – Посчитать количество квадратов в нашем прямоугольнике можно как первым, так и вторым способом, и оба дадут верный результат. Так мы с вами пришли к одному из свойств умножения, которое называется переместительное свойство умножения.

Запомните! От перестановки множителей произведение не меняется.

Это свойство в буквенном виде записывают так:  , где а и b – любые натуральные числа.

– Электроша, вот мы с тобой сейчас умножали небольшие числа. Тут всё понятно, – начал Паша. – А если бы нам нужно было найти произведение, например, 5432 и 305. Как его посчитать?

– Хороший вопрос! – ответил Электроша. – Умножение многозначных натуральных чисел удобнее всего выполнять в столбик. Вы уже умеете умножать в столбик многозначное число на двузначное. Аналогично выполняют умножение любых двух многозначных чисел. Сейчас я вам покажу, как это сделать.

Итак, умножим 5432 на 305. Помним, что для того, чтобы умножить два многозначных числа столбиком, нужно записать их одно под другим таким образом, чтобы цифры соответствующих разрядов оказались на одном уровне, то есть единицы записываем под единицами, десятки – под десятками, сотни – под сотнями и так далее. Будет удобнее считать, если большее число будет записано сверху.

Под нижним числом проведём черту, а слева от записанных чисел поставим знак умножения – «крестик». Затем мы с вами будем перемножать каждую цифру первого числа поочерёдно на цифры второго числа. Начинаем с младшего разряда (самого правого).

2 умножаем на 5. Получаем 10. Под разрядом единиц записываем 0, 1 запоминаем. 3 умножаем на 5. Получаем 15. Да ещё 1, от умножения соседних цифр. Значит, получаем 16. 6 пишем под разрядом десятков, 1 запоминаем. Теперь 4 умножаем на 5. Получаем 20, и ещё 1, которую запоминали. В итоге получаем 21. 1 записываем под сотнями, 2 запоминаем. 5 умножаем на 5. Получаем 25, да ещё 2, что запоминали. Получаем 27. Так мы с вами нашли первое неполное произведение.

Теперь будем искать второе. Нам нужно каждый разряд числа 5432 умножить на 0. А мы уже знаем, что если один из множителей равен нулю, то произведение равно нулю. Получим второе неполное произведение и запишем его под ответом первого неполного произведения, сдвинув на один разряд влево.

Затем перемножим каждую цифру числа 5432 на цифру разряда сотен числа 305. Получаем 16 296. Запишем ответ под ответом второго неполного произведения, сдвинув на один разряд влево.

И осталось сложить все неполные произведения. В итоге получаем 1 656 760.

– Электроша, спасибо! – обрадовались ребята. – Теперь нам понятно, как умножают числа столбиком. Это очень просто и удобно!

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: запишите сумму в виде произведения и вычислите её.

Решение: первая сумма состоит из девяти слагаемых, каждое из которых равно 7. Значит, можем заменить её на произведение 7 и 9. Получим 63.

Следующая сумма состоит из трёх слагаемых, каждое из которых равно 15. Можем заменить сумму на произведение 15 и 3. Получим 45.

И последняя сумма состоит из восьми слагаемых, каждое из которых равно m. Значит, можем заменить сумму на произведение m и 8.

Следующее задание: первое число 405, второе число в 6 раз больше первого и в 5 раз меньше третьего числа. На сколько второе число меньше третьего числа?

Решение: в первом действии вычислим, чему равно второе число. Нам известно, что оно больше первого в 6 раз. Значит, второе число равно 2430.

Во втором действии вычислим, чему равно третье число. Нам известно, что второе число в 5 раз меньше третьего. Значит, третье число равно 12 150.

И осталось ответить на вопрос задачи. Для этого найдём разность третьего и второго чисел. Она равна 9720.

Запишем ответ: второе число меньше третьего на 9720.