Угол. Обозначение углов

Представим себе такую историю.

– Саша, а ты знаешь, что листья на ветке растения всегда располагаются в строгом порядке? – спросил Паша.

– Что значит в строгом порядке? – удивился Саша. – Как числа в натуральном ряду что ли?

– Нет, Саша, листья на ветке растения отстоят друг от друга на определённый угол по или против часовой стрелки – продолжил Паша. – Величина этого угла разная для разных растений.

– Ого! – удивился Саша. – И ведь правда, а я даже и не замечал такого раньше! Но ведь угол – это геометрическое понятие. Зачем растениям углы?

– Такое расположение позволяет листьям растений наиболее эффективно получать влагу и солнечный свет.

– Паша, а ты знаешь, как в математике строят углы? – решил спросить Саша.

– Да, – ответил Паша, – если мы на листе бумаги из одной точки проведём два луча, то получим фигуру, которая называется углом.

– А углы в математике тоже имеют свои названия? – спросил Саша.

– Да, но об этом лучше спросить у Электроши – сказал Паша.

– Ребята, прежде чем я вам расскажу об углах и их обозначениях, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Ну а теперь поговорим об углах, – продолжил Электроша. – Давайте проведём на листе бумаги два луча ВА и ВС с общим началом в точке В.

Запомните! Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

– Значит, угол – это два луча с общим началом? – спросил Саша.

– Всё верно! – подтвердил Электроша.

Лучи называют сторонами угла, а их общее начало – вершиной угла.

Так, например, в угле, который мы с вами построили, лучи ВА и ВС – это стороны угла, а точка В – его вершина.

– Визуально углы делят на «внешний» и «внутренний». Мы же чаще будем работать именно с внутренними углами.

– А как обозначают углы? – спросил Паша.

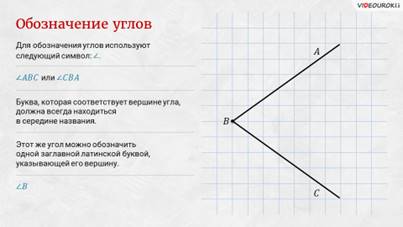
– Для обозначения углов используют следующий символ: . Тогда наш угол можно обозначить так: ∠АВС или ∠СВА. Обратите внимание: называть угол можно с любого края, но не с вершины. Буква, которая соответствует вершине угла, должна всегда находиться в середине названия.

Также этот же угол можно обозначить и короче, одной заглавной латинской буквой, указывающей его вершину. Тогда наш угол можно обозначить так: угол В.

– Посмотрите, я построил три различных угла – продолжил Электроша. – Может, вы сможете их назвать? – спросил он у ребят.

– Первый угол можно обозначить, как ∠PQR – начал Саша, – второй ∠EFT, а третий – ∠KOZ.

– Ещё эти углы можно обозначить так, – продолжил Паша, – ∠Q, ∠F и ∠O.

– Молодцы! – похвалил ребят Электроша. – А теперь посмотрите на следующие углы. Попробуйте сосчитать и назвать все углы на рисунке.

– Угол AOB, – начал Паша, – угол BOC и угол AOC.

– Всё верно! – сказал Электроша. – На нашем рисунке изображены три угла.

– А как же угол О? – спросил Саша.

– Ни один из трёх углов на рисунке нельзя обозначить только одной буквой. У них одна и та же вершина – точка О, но сами углы разные.

– Два угла могут иметь одну общую сторону, – продолжил Электроша. – На нашем рисунке углы AOB и BOC имеют общую сторону ОB. Также в этом случае говорят, что луч ОB проходит между сторонами угла АОC и делит его на два угла: АОB и BОC.

– А теперь давайте проведём небольшой эксперимент. Возьмём лист бумаги, отметим на нём точки M, О, N таким образом, как показано на рисунке. Перегнём лист так, чтобы его две соседние стороны совместились. Затем по линии сгиба проведём луч, например, ОP. Обратите внимание, мы получили два угла: угол MОP и угол NОP, которые совпадают.

Запомните! Два угла называют равными, если они совпадают при наложении.

– То есть углы MОP и NОP равны? – решили спросить ребята.

– Да! – ответил Электроша. – Угол MОP равен углу NОP, а записывают это так: . На рисунке равные углы, как правило, отмечают равным количеством дужек.

– Луч ОP имеет своё название. Такой луч называют биссектрисой угла.

Запомните! Биссектриса делит угол на два равных угла.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: отметьте в тетради точку О и проведите через неё две прямые. На прямых отметьте точки А, B, C и D по разные стороны от точки О. Сколько всего углов у вас получилось? Назовите их.

Решение: на рисунке получилось шесть углов: угол АОB, угол BОC, угол CОD, угол DОА, угол АОC и угол BОD.

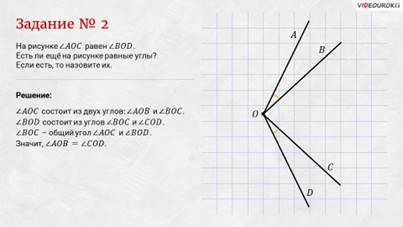
Следующее задание: на рисунке угол АОC равен углу BОD. Есть ли ещё на рисунке равные углы? Если есть, то назовите их.

Решение: угол АОC состоит из двух углов: угла АОB и угла BОC. Аналогично и угол BОD состоит из углов BОC и CОD. Видим, что угол BОC общий угол углов АОC и BОD. Значит, углы АОB и CОD равны тоже.

– Ребята, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.

Итак, масса 4 персиков и 3 яблок вместе 425 г. А 3 персика и 4 яблока (вместе) имеют общую массу 345 г. Все персики имеют одинаковую массу. Яблоки тоже весят одинаково. Какова общая масса одного персика и одного яблока (вместе)?

Решение: так как по условию задачи 4 персика и 3 яблока вместе весят 425 г, а также 3 персика и 4 яблока вместе весят 345 г, то можем узнать, сколько будут весить 7 персиков и 7 яблок вместе, то есть к 425 прибавим 345, получим 770 г. А теперь можем найти вес одного персика и одного яблока вместе: 770 разделим на 7 и получим 110 г.

Ответ: 110 грамм общая масса одного персика и одного яблока.