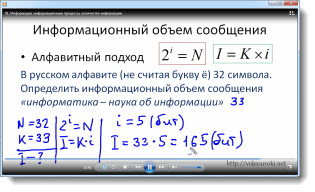
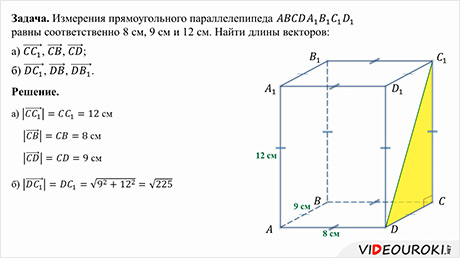
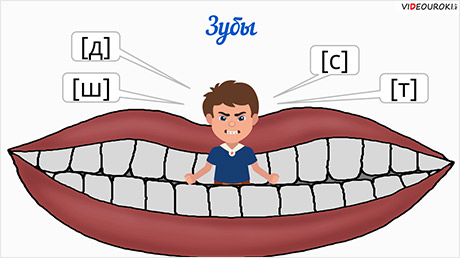
Давайте представим себе такую историю.
– Ну и как же мне здесь разобраться? – бормотал Саша.
– Саша, что случилось? – спросил Паша.
– Мама, прежде чем уйти на работу, сказала, что купила один очень важный предмет, который мне пригодится на уроках математики.
– Здорово! – обрадовался за друга Паша. – И что это за предмет такой важный?
– Вот в этом и проблемка – загрустил Саша. – Мама спрятала этот предмет, но, чтобы я его нашёл, она подготовила инструкцию, где написано, что мне нужно сделать.
– Так давай я тебе помогу! – предложил Паша. – Показывай свою инструкцию!
– Смотри! – обрадовался Саша.

– В первом пункте написано, что я должен сделать 10 шагов прямо.
– Ну и что тут сложного? – удивился Паша.
– Ничего! – ответил Саша. – Шаги то я сделал, а вот в следующих пунктах сказано, что я должен повернуть вправо на величину, равную прямому углу, а затем сделать ещё 5 шагов. Что значит повернуть вправо на величину, равную прямому углу? Что это за величина-то такая и что за прямой угол?
– Да… проблемка! – задумался Паша. – Давай спросим у Электроши. Он точно сможет нам помочь!
– Ребята, прежде чем я вам расскажу об измерении углов, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Ну а теперь поговорим об измерении углов, – предложил Электроша. – Но для начала давайте вспомним, что вообще называют углом.
– Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки – сказал Саша.

– Молодец! – похвалил Сашу Электроша. – Вы уже знаете, как измеряют отрезки. Скажите, что значит измерить отрезок?
– Измерить отрезок – означает подсчитать, сколько единичных отрезков в нём помещается – сказал Паша. – Для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и другие).

– Правильно! – подтвердил Электроша. – Тогда, как вы думаете, что значит измерить угол?
– Ну, наверное, – начал Паша, – измерить угол – означает подсчитать, сколько единичных углов в нём помещается.
– Верно! – сказал Электроша. – Однако для измерения углов у нас пока ещё нет такого единичного угла. Но мы можем сами его создать. И сейчас я вам покажу, как это сделать.
– Давайте нарисуем круг и разделим его на 360 равных частей. Угол, образованный двумя соседними лучами, выбирают за единицу измерения. И такой уголок принято называть градусом. Кстати, градус происходит от латинского слова и переводится как «шаг», «ступенька».

– То есть 1 градус – это и есть наш единичный угол, с помощью которого мы сможем определить величину нужного нам угла? – решили уточнить мальчишки.
– Правильно! – сказал Электроша. Запомните! Градус – это общепринятая единица, которой пользуются для измерения углов. Для обозначения градусов в тексте используют вот такой знак: о.

Так как мы с вами делили круг на 360 равных частей, то угол, равный плоскости круга, составляет 360 градусов, и называется такой угол полным углом.

– Электроша, а если полный угол разделить пополам, мы получим половинный угол? – поинтересовался Паша.
– Если плоскость круга разделить на 2 равные части, то плоскость одного полукруга составит угол в 180 градусов.

Запомните! Угол, равный полуплоскости круга, составляет 180 градусов и называется развёрнутым углом. Обратите внимание, стороны развёрнутого угла образуют прямую.

– А если бы мы разделили круг на 4 части? – спросил Саша.
– Если плоскость круга разделить на 4 равные части, то плоскость одной части составит угол в 90 градусов.

Запомните! Угол, равный четвёртой части круга, составляет девяноста
градусов и называется прямым углом. Прямой угол обозначают вот
таким значком:  .
.

Существуют и другие виды углов.
Так, например, угол, градусная мера которого меньше 90 градусов, называют острым.
Угол, градусная мера которого больше 90 градусов, но меньше 180 градусов, называют тупым.

– Электроша, спасибо! Теперь я понял, что значит повернуть вправо на величину, равную прямому углу. Сейчас я быстренько найду предмет, который спрятала мама.
– Смотрите, какую необычную линейку купила мне мама! – воскликнул Саша. – Разве такая линейка пригодится на уроках математики?

– Саша, конечно, пригодится! – успокоил мальчика Электроша. – Такую линейку используют для измерения углов, а также для построения угла нужной величины. А называется эта линейка «транспортир».
– Вообще, этот инструмент может иметь разный внешний вид, но у любого транспортира есть шкала, которая расположена на полуокружности.

Давайте поближе рассмотрим Сашин транспортир.

Посмотрите, внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части – полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов. Каждое деление шкалы транспортира равно 1 градусу. Центр шкалы отмечен штрихом или отверстием.
– Электроша, а как измерять углы транспортиром? – уточнили ребята.
– Это совсем несложно, – сказал Электроша. – Давайте рассмотрим алгоритм измерения углов на примере.
Итак, найдём величину угла АОВ. Для начала
совместим вершину угла с центром транспортира. Затем расположим транспортир
так, чтобы одна из сторон угла прошла по линейке. У нас это сторона ОВ. А
теперь найдём штрих на шкале, через который проходит вторая сторона угла. Этот
штрих и укажет градусную меру (величину) нашего угла. Посмотрите, в нашем
случае градусная мера угла АОВ равна 60 градусам. Записывают это так:  .
.

– Электроша, ты говорил, что с помощью транспортира можно строить углы, – решил уточнить Саша. – Научишь нас?
– Конечно! – обрадовался Электроша. – Давайте рассмотрим алгоритм построения углов на конкретном примере.
– Итак, давайте построим угол АВС, равный 120 градусам. Для начала отметим произвольную точку и обозначим её буквой В. Затем начертим луч с началом в точке В и на нём отметим точку А. Получим луч ВА. Теперь приложим к этому лучу транспортир так, чтобы его центр совпал с точкой В, а сам луч ВА прошёл через начало отсчёта на шкале. Затем на этой же шкале найдём штрих, который соответствует 120 градусам. За штрихом отметим точку и обозначим её буквой С. Осталось провести луч ВС. Вот так мы с вами построили угол АВС, равный 120 градусам.

– Как видите, всё очень легко! Нужно просто один раз попробовать и всё обязательно получится!
– А теперь скажите, какие углы мы называем равными? – спросил у ребят Электроша.
– Два угла называют равными, если они совпадают при наложении, – ответили мальчишки.

– Молодцы! – похвалил ребят Электроша. – Так как равные углы полностью совмещаются при наложении, то можем сделать вывод, что равные углы имеют равные градусные меры. А значит, из двух неравных углов большим будем считать тот, градусная мера которого больше, и, соответственно, меньшим тот, градусная мера которого меньше.
– Посмотрите, я нарисовал 3 разных угла, – продолжил Электроша. – Что вы можете сказать об их величинах?
– Даже не измеряя транспортиром, видно, что угол MNP больше угла QST, – начал Паша. – Ещё можно сказать, что угол EFG меньше угла MNP.
– А если измерить эти углы, – продолжил Саша, то увидим, что угол QST равен углу EFG.

– Ещё вам следует знать свойство величины угла.
Запомните! Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC. Записывают это свойство так:  .
.

– Вот, например, градусная мера угла ABD равна 30 градусам, а градусная мера угла DBC равна 20 градусам. Тогда чему будет равна градусная мера угла ABC?
– По свойству величины угла, – начал Паша, – мы должны сложить величины углов ABD и DBC. Тогда величина угла ABC равна 50 градусам.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.
Итак, угол ABC разделён лучом BD на два угла ABD и DBC так, что градусная мера угла ABD равна 29 градусам, а градусная мера угла DBC равна 61 градусу. Постройте угол ABC и определите его вид.
Решение: для начала нам нужно выяснить градусную меру угла ABC. Применяя свойство величины угла, получаем, что угол ABC равен 90 градусов. Теперь построим этот угол. И осталось определить его вид. Мы знаем, что угол, который составляет 90 градусов, называется прямым углом. Значит, наш угол ABC – прямой.


 Получите свидетельство
Получите свидетельство Вход
Вход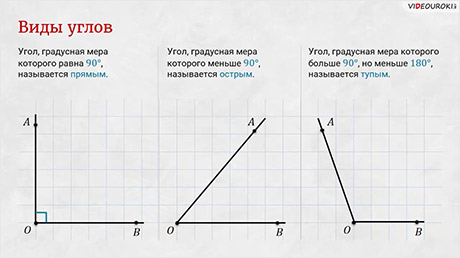



 0
0 4868
4868