Давайте с вами посмотрим на прямоугольную проекцию главного вида некоторой детали. Попробуйте найти эту деталь среди представленных наглядных изображений.

Они все подходят? Да, вы правы — все представленные детали. А какой вывод из этого следует? Правильно. Одна проекция, даже главный вид, не всегда однозначно определяет форму и конструкцию изображаемого предмета. Различные по форме предметы могут образовывать одинаковые проекции.
Для того чтобы получить представление о форме объёмного предмета, проецирование выполняют на две взаимно перпендикулярные плоскости проекций: горизонтальную Н и фронтальную V. Плоскости проекций V и Н пересекаются по оси «Икс» (Х), которую ещё называют осью проекций.

Давайте с вами вспомним, что при проецировании объекта на горизонтальную плоскость проекций получают его горизонтальную проекцию (её ещё называют видом сверху). А при проецировании на фронтальную плоскость проекций получают фронтальное изображение объекта. Чаще всего фронтальное изображение является главным видом объекта, который также называют видом спереди.
Рассмотрим модель двугранного угла: горизонтальная плоскость проекций Н расположена под углом 90° к фронтальной плоскости проекций V. Плоскости проекций V и Н пересекаются по оси Х.
Проецируемая деталь расположена в двугранном углу параллельно горизонтальной и фронтальной плоскостям, на которых получают проекции — фронтальную и горизонтальную.

Обратите внимание: каждая проекция получена посредством проецирующих лучей, проходящих через вершины детали и направленных перпендикулярно каждой плоскости проекций (например, через вершину А проходят два проецирующих луча: один — это A-а' перпендикулярно плоскости V, другой — А-а перпендикулярно плоскости Н.
Чтобы получить чертёж детали, горизонтальную плоскость Н поворачивают вокруг оси X до совмещения с фронтальной плоскостью V. Совмещение двух плоскостей проекций позволяет получить чертёж с изображениями двух видов проецируемого предмета, расположенными друг под другом и соединёнными линиями проекционной связи, которые являются проекциями проецирующих лучей.

Помните! При построении чертежа горизонтальную проекцию предмета Н всегда располагают под фронтальной V.
Прямоугольное проецирование ещё называют ортогональным. Основоположником ортогонального проецирования считается французский учёный Гаспар Монж.
Метод Монжа — это метод прямоугольного проецирования на две взаимно перпендикулярные плоскости проекций. Линия пересечения двух плоскостей проекций называется осью проекций. Получаемые при этом ортогональные проекции (вид спереди и сверху), помещённые в одну плоскость, образуют комплексный чертёж, или эпюр Монжа.
Гаспар Монж положил начало развитию науки «Начертательная геометрия».

Конечно, основы начертательной геометрии возникли ещё в глубокой древности. Так, греческий геометр Евклид и римский архитектор Витрувий внесли большой вклад в развитие методов построения изображений пространственных форм на плоскости.
Бурное развитие архитектуры, живописи и скульптуры в эпоху Возрождения создало условия для развития методов построения изображений пространственных форм на плоскости. В это время вводится целый ряд основных понятий: центральное проецирование, картинная плоскость, дистанция, главная точка, линия горизонта, дистанционные точки и так далее.

Одним из первых, кто применял перспективу в своих работах, был итальянский архитектор и учёный Филиппо Брунеллески. В трактате по перспективе Леонардо да Винчи приводятся примеры применения перспективных изображений, сведения о воздушной и линейной перспективе и теории светотени. Большой вклад в теорию перспективы внесли Альбрехт Дюрер, Гвидобальдо дель Монте, Жерар Дезарг.

Но только в 1798 году французский инженер и учёный Гаспар Монж сформулировал главные элементы теории построения графических изображений. Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остаётся основным методом составления технических чертежей.
Давайте посмотрим, как происходит построение двухпроекционного чертежа на примере простейшего геометрического объекта — точки.
Итак, вначале из точки А на плоскости V и H опускают перпендикуляры и получают проекции точки А: а — горизонтальная проекция и а′ — фронтальная проекция.
Затем мысленно удаляют точку А и поворачивают горизонтальную плоскость Н вокруг оси Х на угол 90° вниз до совмещения с фронтальной плоскостью V.

Посмотрите, проекции а и а′ расположились на одной прямой а′а″. Эта линия а′а″ и есть линия проекционной связи.
Помните! Фронтальная и горизонтальная проекции точки всегда находятся на перпендикуляре к оси проекций Х.
Если комплексный чертёж выполнен с осью X, его называют осным чертежом. Часто ось X не проводят на чертеже, а только подразумевают, что она присутствует. В этом случае чертёж называют безосным. Построение безосного и осного чертежей аналогично. Это касается:
1) соблюдения проекционной связи видов детали — вид сверху всегда располагается чётко под главным видом;
2) нанесения размеров — размеры длины детали и её элементов наносят всегда параллельно оси «Икс» (X) как можно ближе к тому элементу, размер которого указывается. Размеры высоты детали наносят только на главном виде. А размеры её ширины — только на горизонтальной проекции, то есть на виде сверху.
На чертеже любое изображение предмета всегда двумерное: фронтальная проекция передаёт его длину и высоту, а горизонтальная — длину и ширину.
Запомните! На главном виде всегда наносят размеры длины и высоты детали, а на виде сверху — длины и ширины. Причём вначале наносят размеры по длине детали: элементов, координирующие, габаритные. Затем — в той же последовательности — по высоте, потом — по ширине.

В пространстве геометрические тела могут располагаться относительно плоскостей проекций по-разному — перпендикулярно к горизонтальной или фронтальной плоскости проекций, параллельно им. Но при любом их положении всегда получают два изображения — вид спереди и вид сверху каждого геометрического тела. Проекциями геометрических тел всегда являются плоские геометрические фигуры.

Ещё раз повторим! Горизонтальные проекции точек обозначаются строчными (малыми) буквами русского или латинского алфавита: на горизонтальной плоскости — малой буквой, а на фронтальной — той же малой буквой, но со штрихом.

 Получите свидетельство
Получите свидетельство Вход
Вход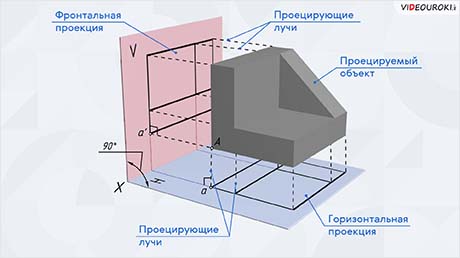




 991
991

