Золотое сечение

Математическое исследование «Золотое сечение»

Цели: изучить основные понятия по теме «Золотое сечение»; повторить понятие «отношение», «пропорция», «основное свойство пропорции» и др; изучить «идеальные» пропорции тела.

Задачи

1. Ознакомиться с понятием Золотое сечение.

2. Показать математические свойства золотой пропорции;

3. Научиться делить целое в отношении золотой пропорции.

4. Проследить этапы возникновения «золотого сечения» в науке.

5. Рассмотреть применение золотой пропорции в жизни и ее практическую значимость.

Оборудование: сантиметровая лента, линейка, раздаточный материал (таблица для измеренных данных, распечатанный наглядный материал)

Ход занятия

1. Организационный момент (тема, цели и задачи урока)

2. Введение.

Золотое сечение. Краткая история и факты.

Золотое сечение – гармоническая пропорция.

В математике пропорцией (лат. proportio) называют равенство двух отношений:

a : b = c : d.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему:

a : b = b : c или c : b = b : a.

Узнаем краткие факты.

СМ. видео -фрагмент, если нет тсо-читайте текст.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа.

Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке или относят появление этого термина к XVI веку, самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика» , в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам, хотя некоторые авторы утверждают обратное. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги, Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.  Марио Ливио считает, что он получил популярность в устной традиции около 1830 года. В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.

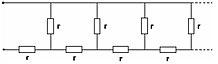
Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке, имеет общее сопротивление (между двумя левыми концами) φ·r.

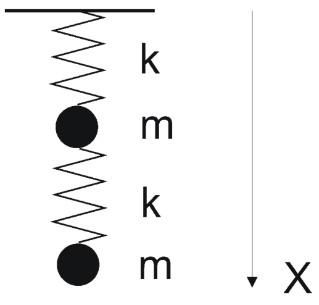
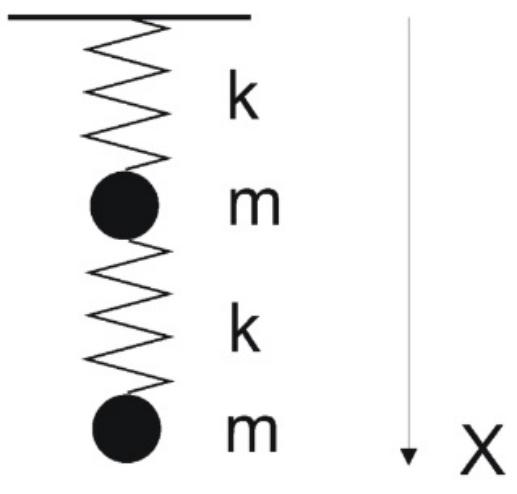
Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

Золотое сечение и гармония в искусстве

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

• Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.

• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д., а также многие другие

1. Выполнение заданий.

Переходим к практической части нашего занятия

Задание 1

Найдите закономерность и продолжите ряд 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...это числа Фибоначчи

Задание 2

Найдите отношения 5 к 3, 8 к 5, 13 к 8. Ответ округлите до десятых. Можно ли сказать, что эти отношения приблизительно равны?

1. Физкультминутка

Нам радостно, нам весело!

Смеемся мы с утра.

Но вот пришло мгновенье,

Серьезным быть пора.

Глазки прикрыли, ручки сложили,

Головки опустили, ротик закрыли.

И затихли на минутку,

Чтоб не слышать даже шутку,

Чтоб не видеть никого, а

А себя лишь одного!

1. Выполнение заданий.

Задание 3

Исследование:

a) Измерьте расстояние от пола до пояса в см.

б) Измерьте свой рост в см.

в) Измерьте расстояние от подбородка до верхней точки губ.

г) Измерьте длину лица (измерение проводить по середине лица) от подбородка до волос на лбу.

д) Измерьте расстояние между зрачками.

е) Измерьте расстояние между бровями.

Занесите данные в таблицу.

Найдите отношения (разделите):

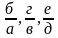
Получилось ли у вас золотое сечение? Какие выводы можно сделать?

1. Домашнее задание: проверить условия Золотой пропорции на своих родственниках. Данные занесите в таблицу.

2. Давайте подведем итоги.

Рефлексия

В графу «+» – «плюс» записывается все, что понравилось на уроке, информация и формы работы, которые вызвали положительные эмоции, либо, по мнению учащегося, могут быть ему полезны для достижения каких-то целей.

В графу «-» – «минус» записывается все, что не понравилось на уроке, показалось скучным, осталось непонятным.

В графу «֎» – «интересно» обучающиеся вписывают все любопытные факты, о которых узнали на уроке, и что бы еще хотелось узнать по данной проблеме, вопросы к учителю.

Домашнее задание

Домашнее задание

Домашнее задание