Конспект интегрированного урока по математике и ИЗО "Пропорциональные отрезки и золотое сечение"

Цель:

1. Ввести понятие пропорциональных отрезков и понятие золотого сечения.

2. Показать применение золотого сечения в изобразительном искусстве.

3. Развивать познавательную активность, мышление, расширять кругозор.

Оборудование: мультимедийный проектор, чертёжные принадлежности, листы белой бумаги формата А4.

Этапы урока.

1. Оргмомент. Вступительное слово учителя (1мин)

2. Актуализация знаний обучающихся (5мин)

3. Изучение нового материала (10 мин)

4. Доклады обучающихся (14мин)

5. Практическая работа (12мин)

6. Итоги урока. Рефлексия (3мин)

Ход урока.

1. Оргмомент. Вступительное слово учителя (1мин)

Учитель :Сегодня мы познакомимся с понятиями пропорциональных отрезков и “золотого сечения”, научимся находить “золотое сечение” отрезка АВ алгебраически, с помощью решения квадратного уравнения, а также посмотрим, как это можно сделать геометрически. При этом мы узнаем много интересных фактов из области культуры и искусства.

2. Актуализация знаний обучающихся (5мин)

Учитель:

- Что называют отношением двух чисел? Что показывает это отношение?

- Отношение АВ к СD равно 2 :7. О чём это говорит? Найдите отношение СD к АВ.

- Что называют пропорцией? Верны ли пропорции 15:18 = 25:30; 18:3=5:30 ?

- В пропорции a:b=c:d назовите средние и крайние члены. Сформулируйте основное свойство пропорции.

3. Изучение нового материала (10 мин)

Учитель:

- Ввести понятие отношения отрезков.

Определение: Отношением отрезков АВ и СD называется отношение их длин, т. е. АВ:СD

- Ввести понятие пропорциональных отрезков.

Определение: Отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁, если AB/А₁В₁= CD/С₁D_1.

Например, если АВ=12см, СD=18см, А₁В₁=2см и С₁D₁=3см, то AB/А₁В₁= CD/С₁D₁, то есть отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D_1.

- Ввести понятие золотого сечения

Пусть дан отрезок АВ, отметим на этом отрезке точку С так, чтобы СВ:АС=АС:АВ. Такое деление отрезка называют золотым сечением. При этом меньшая часть отрезка относится к большей так, как большая часть относится ко всему отрезку.

Начертим отрезки и проверим выполняется ли в их делении золотое сечение. 

Сравним 2/3 и 3/5; 3/5 и 5/8.

Если мы 2 : 3, то получим приближено 0, 6

3 : 5 = 0, 6

3/5 = 0,6

5/8 прибл. = 0,6.

Таким образом, в изображенных отрезках меньшая часть относится к большей приближенно также, как большая часть относится ко всему отрезку.

4. Доклады обучающихся.

Применение золотого сечения в изобразительном искусстве. (14мин)

Учитель: А сейчас мы углубимся в историю. Оказывается, при изображении пространственных фигур немаловажную роль играет соотношение различных частей одной и той же фигуры. Давайте послушаем доклады на эту тему.

1 обучающийся: При изображении пространственных фигур важное место занимает вопрос о нахождении наилучшего соотношения неравных частей, составляющих вместе единое целое. Его решение связывают с именем Пифагора, который установил, что наиболее совершенным делением целого на две неравные части является такое деление, при котором меньшая часть так относится к большей, как большая часть относится ко всему целому.

В Древней Греции такое деление называлось гармоническим отношением, а в эпоху Возрождения его называли золотым сечением. Термин «золотое сечение» ввёл великий художник, учёный и изобретатель Леонардо да Винчи (1452-1519). В 1509 году монах Лука Пачоли, друг Леонардо, написал целую книгу о золотом сечении, которую он назвал «Божественная пропорция». Леонардо да Винчи выполнил иллюстрации к этой книге. В ней воздействие божественной пропорции на человека называлось «чудесным, неизъяснимым, возвышенным и непостижимым».

Учитель: Давайте более подробно ознакомимся с этим понятием «золотое сечение».

1 обучающийся: Сначала выясним, каким числом выражается золотое сечение. Для этого выберем произвольный отрезок и примем его длину за единицу. Разобьем этот отрезок на две неравные части. 

Весь материал - в документе.

Математика и ИЗО

Интегрированный урок

Выполнила: Лукьянчикова О.М.

учитель математики

МБОУ СОШ№27

г.Курска

Тема: Пропорциональные отрезки и золотое сечение

(геометрия 8 класс)

Цель:

1. Ввести понятие пропорциональных отрезков и понятие золотого сечения

2. Показать применение золотого сечения в изобразительном искусстве

3. Развивать познавательную активность, мышление, расширять кругозор.

Оборудование: мультимедийный проектор, чертёжные принадлежности, листы белой бумаги формата А4.

Этапы урока

1. Оргмомент. Вступительное слово учителя (1мин)

2. Актуализация знаний обучающихся (5мин)

3. Изучение нового материала (10 мин)

4. Доклады обучающихся (14мин)

5. Практическая работа (12мин)

6. Итоги урока. Рефлексия (3мин)

Ход урока

1.Оргмомент. Вступительное слово учителя (1мин)

Учитель :Сегодня мы познакомимся с понятиями пропорциональных отрезков и “золотого сечения”, научимся находить “золотое сечение” отрезка АВ алгебраически, с помощью решения квадратного уравнения, а также посмотрим, как это можно сделать геометрически. При этом мы узнаем много интересных фактов из области культуры и искусства.

2. Актуализация знаний обучающихся (5мин)

Учитель:

-Что называют отношением двух чисел? Что показывает это отношение?

-Отношение АВ к СD равно 2 :7. О чём это говорит? Найдите отношение СD к АВ.

-Что называют пропорцией? Верны ли пропорции 15:18 = 25:30; 18:3=5:30 ?

-В пропорции a:b=c:d назовите средние и крайние члены. Сформулируйте основное свойство пропорции.

3. Изучение нового материала (10 мин)

Учитель:

-Ввести понятие отношения отрезков.

Определение: Отношением отрезков АВ и СD называется отношение их длин, т.е. АВ:СD

-Ввести понятие пропорциональных отрезков.

Определение: Отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁, если

.

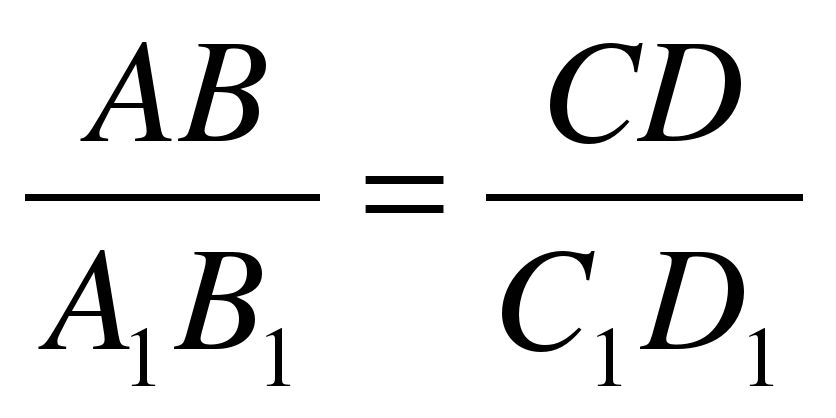Например, если АВ=12см, СD=18см, А₁В₁=2см и С₁D₁=3см, то 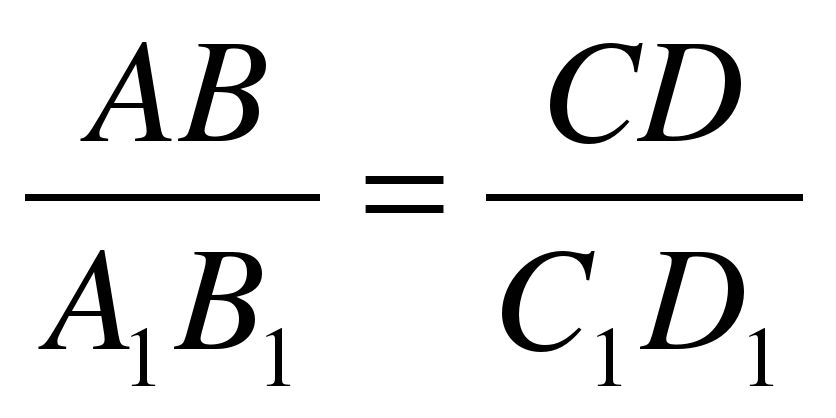, то есть отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁ .

-Ввести понятие золотого сечения

Пусть дан отрезок АВ, отметим на этом отрезке точку С так, чтобы СВ:АС=АС:АВ. Такое деление отрезка называют золотым сечением. При этом меньшая часть отрезка относится к большей так, как большая часть относится ко всему отрезку.

Начертим отрезки и проверим выполняется ли в их делении золотое сечение.

5 см

2 см 3 см

8 см

3 см 5 см

Сравним ; .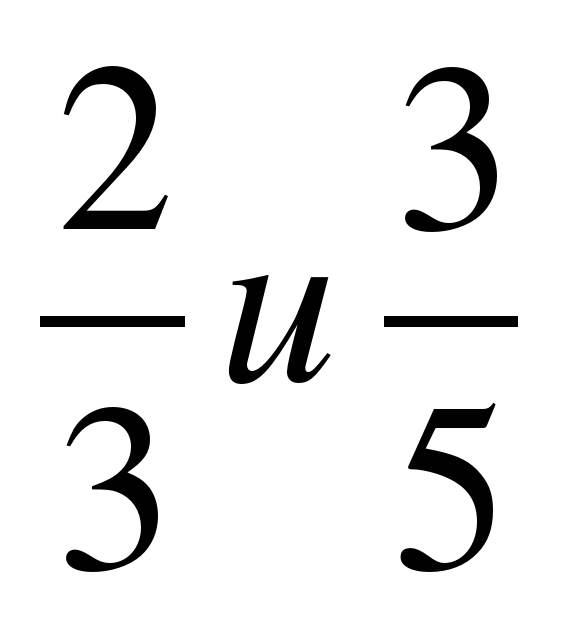

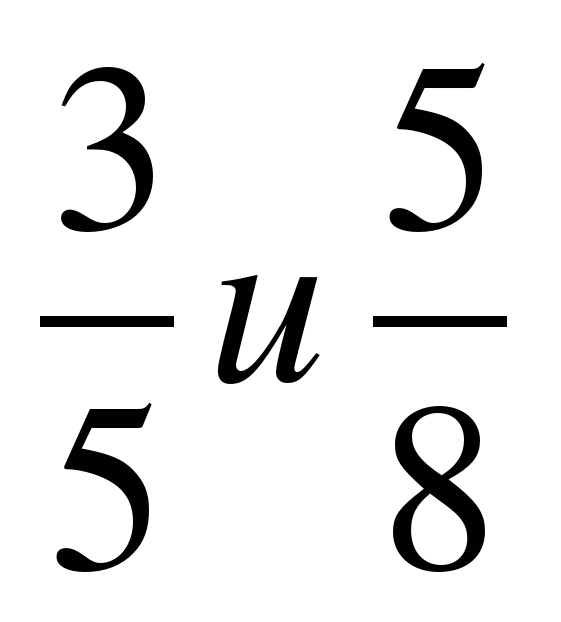Если мы 2 : 3, то получим приближено 0,6

3 : 5 = 0,6

.

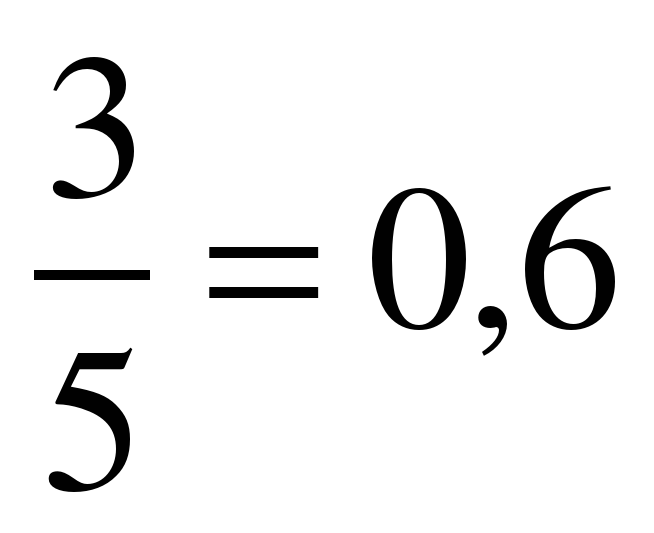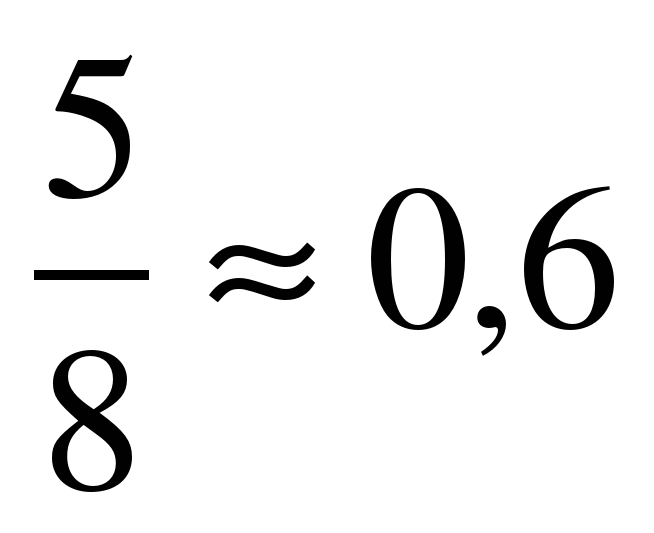
Таким образом, в изображенных отрезках меньшая часть относится к большей приближенно также, как большая часть относится ко всему отрезку.

4. Доклады обучающихся.

Применение золотого сечения в изобразительном искусстве. (14мин)

Учитель: А сейчас мы углубимся в историю. Оказывается, при изображении пространственных фигур немаловажную роль играет соотношение различных частей одной и той же фигуры. Давайте послушаем доклады на эту тему.

1 обучающийся: При изображении пространственных фигур важное место занимает вопрос о нахождении наилучшего соотношения неравных частей, составляющих вместе единое целое. Его решение связывают с именем Пифагора, который установил, что наиболее совершенным делением целого на две неравные части является такое деление, при котором меньшая часть так относится к большей, как большая часть относится ко всему целому. В Древней Греции такое деление называлось гармоническим отношением, а в эпоху Возрождения его называли золотым сечением. Термин «золотое сечение» ввёл великий художник, учёный и изобретатель Леонардо да Винчи (1452-1519). В 1509 году монах Лука Пачоли, друг Леонардо, написал целую книгу о золотом сечении, которую он назвал «Божественная пропорция». Леонардо да Винчи выполнил иллюстрации к этой книге. В ней воздействие божественной пропорции на человека называлось «чудесным, неизъяснимым, возвышенным и непостижимым».

Учитель: Давайте более подробно ознакомимся с этим понятием « золотое сечение».

1 обучающийся: Сначала выясним, каким числом выражается золотое сечение. Для этого выберем произвольный отрезок и примем его длину за единицу. Разобьем этот отрезок на две неравные части. Большую часть обозначим через х, тогда меньшая часть равна 1-х. По определению золотого сечения выполняется равенство:

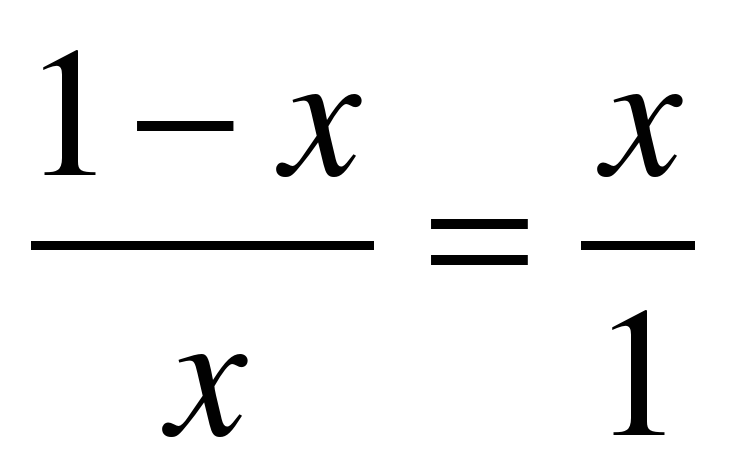, при этом .

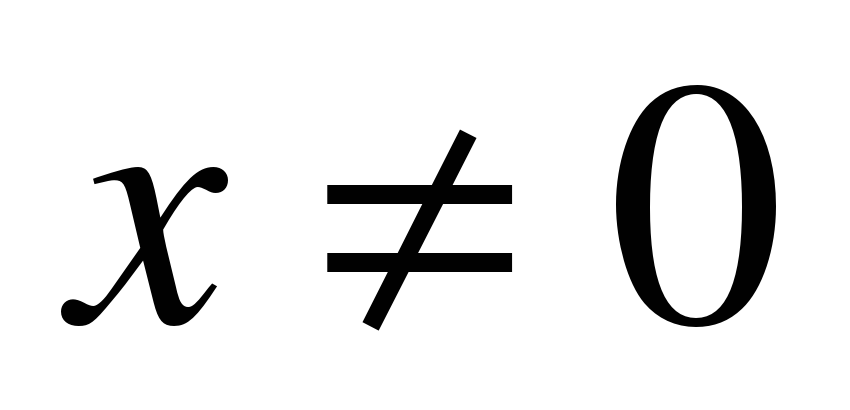Мы получим уравнение относительно х, которое легко свести к квадратному:

.

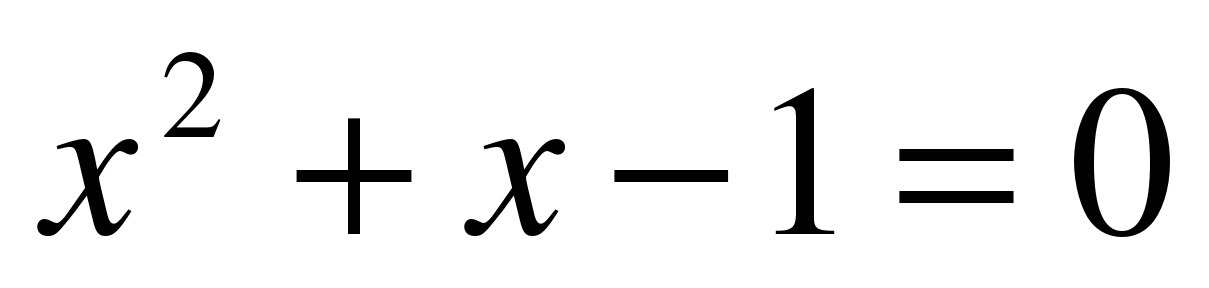Положительный корень этого уравнения равен:

.

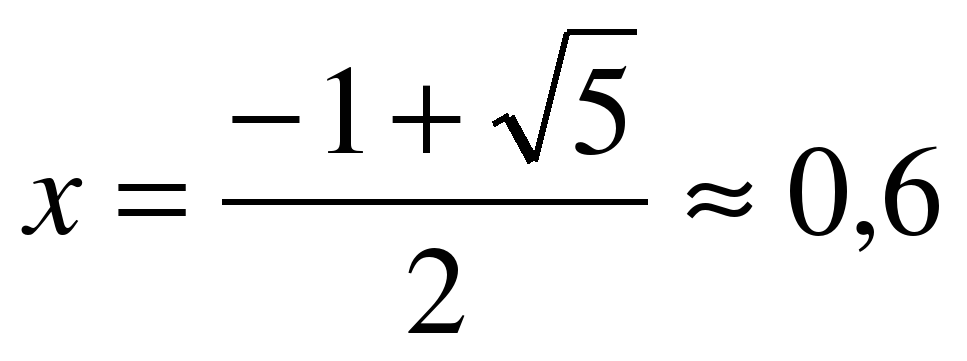Итак, если длина исходного отрезка равна 1 , тот его большая часть при золотом сечении равна примерно 0,6.

Полученное число обозначается буквой. Это первая буква в имени великого скульптора Фидия, который часто использовал золотое сечение в своих произведениях. Самым знаменитым из них была статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.

Учитель: А теперь давайте посмотрим, как золотое сечение использовалось в живописи, скульптуре, архитектуре и т.д.

3 обучающийся: Так как пропорции золотого сечения создают впечатление гармонии и красоты, с древних времён скульпторы, архитекторы, художники, использовали и используют золотое сечение в своих произведениях. Большинство статуй ( в частности статуя Венеры, представленная здесь) состоят из частей, которые делятся в золотом сечении. Причём делится не только вся статуя, но и отдельные её части. Одно из красивейших произведений древнегреческой архитектуры Парфенон в Афинах (V век до нашей эры) содержит в себе золотые пропорции. Так отношение высоты здания к его длине равно . Если произвести деление высоты Парфенона по золотому сечению, то получим те или иные выступы здания.

Учитель: И ещё несколько интересных фактов продолжают развивать тему золотого сечения.

4 обучающийся: Прямоугольник, стороны которого находятся в золотом отношении, иногда называют золотым прямоугольником. Золотые прямоугольники обладают многими интересными свойствами. Если, например, от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник, меньших размеров. Если этот процесс продолжить, то получим так называемые вращающиеся квадраты, и весь прямоугольник, оказывается составленным из этих квадратов. Если соединить противоположные вершины квадратов плавной кривой. То получим кривую, называемую «золотой спиралью». Эту кривую можно заметить в созданиях природы. Например, раковины моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из наиболее распространённых пауков, эпейра, сплетает свою паутину по золотой спирали. Природа повторяет свои находки, как в малом, так и в большом. Например, семечки подсолнуха располагаются по золотой спирали точно так же, как закручиваются многие галактик, в частности и галактика Солнечной системы.

5. Практическая работа (12мин)

Учитель: А теперь давайте познакомимся, как выполняется “Золотое сечение” геометрическим способом, с помощью циркуля и линейки. Делать построения будем на листах белой бумаги формата А4.

Задание 1 : Построить золотой прямоугольник.

1. Начертим квадрат и разделим его на два равных прямоугольника.

2. В одном из прямоугольников проведем диагональ АВ.

3. Циркулем проведем окружность радиуса АВ с центром в точке А.

4. Продолжим основание квадрата до пересечения с дугой в точке Р и проведем под прямым углом вторую сторону искомого прямоугольника.

Измерьте линейкой длины сторон построенного прямоугольника MNKP и вычислите отношения большей стороны к меньшей. (Отношение сторон должно быть примерно равно 1,6).

Но как же разделить отрезок в золотом отношении?

Задание 2: Разделить отрезок в золотом отношении.

С помощью непосредственных измерений сделать это не возможно, поскольку число –иррациональное. Древние мастера использовали циркуль и линейку, причем были найдены различные способы построения. Рассмотрим один из них, самый простой.

Пусть дан отрезок АВ , и надо осуществить его “золотое сечение”. Проведем перпендикуляр к отрезку АВ (будем считать, что АВ=1) и отложим на нем отрезок ВД = 2АВ. Тогда =АД. Из точки Д проведем окружность радиусом ДК, где ДК=АВ.

Тогда . Теперь проведем окружность с центром в точке А радиусом   Она пересечет отрезок АВ в точке С золотого сечения, поскольку АС= .

Итак, найдена, казалось бы, совершенно ординарная точка на обычном отрезке. А между тем ею обеспечивается присутствие красоты, соразмерности всех частей.

1. Итоги урока. Рефлексия (3мин)

Учитель: Что нового вы узнали на уроке? Какие отрезки называются пропорциональными? Что такое золотое сечение? Где оно применяется?

Рефлексия.

Что получилось?

Что не получилось?

Что было самое трудное?

Понравились ли задания?

В завершении урока домашнее задание:

Найти «золотое сечение» у себя в доме. Сделать схематический рисунок, расчеты и оформить на альбомном листе. (Сдать своему учителю математики).