Практическая работа
Решение задач по теме: «Законы термодинамики»
Задача. 1. Молекулы азота занимают объем V1 =2 м3 и находится под давлением p1=1 атм. Газ нагревают, причем нагрев ведут сначала при постоянном объеме до давления p2=5 атм, а затем при постоянном давлении до объема V2=4 м3. Масса азота 3 кг. Газ идеальный. Определить изменение внутренней энергии газа, совершенную им работу, количество тепла, переданное газу.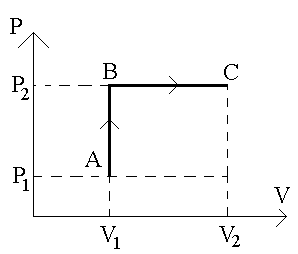
Решение. Задачи такого типа решать проще, если все переходы газа из одного состояния в другое представлены графически. На рисунке оба процесса перехода изображены в системе координат PV. Прямая AB – изохора, идет нагревание газа от T1 до T2 c соответствующим увеличением давления от p1 до p2 при постоянном объеме V1. В этом процессе происходит увеличение внутренней энергии газа целиком за счет тепла (см. таблицу). Прямая BC – изобара. Ей соответствует повышение температуры, а, следовательно, и изменение внутренней энергии. Кроме того, газ, расширяясь, совершает работу.
Полное изменение энергии складывается из изменения энергии U1 на участке AB и изменения энергии U2 на участке BC
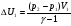 ,
,  .
.
Общее изменение внутреннее энергии есть сумма U1+U2:
 .
.
Работа, совершаемая газом, графически определяется площадью под кривой ABC в системе координат PV, и складывается из работ на участках AB и BC. В нашем случае, работа на участке AB не производится, следовательно, вся работа над газом будет определяться работой на участке изобарического процесса BC
 .
.
Количество поглощенного тепла определяется по первому началу термодинамики
 .
.
Подставив числовые данные в формулы, определим соответственно
A= 1,01·106Дж; U=5·106Дж; Q=6,01·106Дж.
Задача 2. Установите соотношения между молярными теплоемкостями CP и СV для идеального газа.
Решение. Пусть один моль идеального газа находится в цилиндре с поршнем. Закрепив поршень, повысим температуру газа на dT. Поскольку объем газа остается постоянным, то количество тепла, необходимое для такого нагревания, равно (Q)V=CVdT. Так как при этом не производится работа, то это тепло равно приращению внутренней энергии газа СVdT=dU. Проведем теперь с тем же газом другой опыт. Пусть начальное состояние будет тем же самым, что и в предыдущем опыте, но поршень не закреплен, а может свободно перемещаться под постоянным внешним давлением p. По определению теплоемкости CP для повышения температуры газа на величину dT требуется тепло (Q)Р=CРdT. При этом газом будет совершена работа А=pdV. Так как давление постоянно, то для моля идеального газа из уравнения Менделеева – Клапейрона:
|
| (1.12) |
следует, что A=d(pV)=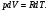 А так как внутренняя энергия газа зависит только от температуры, то она изменится на столько же, на сколько и в предыдущем опыте. Таким образом:
А так как внутренняя энергия газа зависит только от температуры, то она изменится на столько же, на сколько и в предыдущем опыте. Таким образом:  . Подставив вместо dU=RdT, получаем
. Подставив вместо dU=RdT, получаем
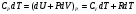 .
.
Сократив правую и левую часть уравнения на конечную величину dT, получим уравнение Роберта Майера
|
| (1.13) |
Для одного моля газа с i степенями свободы внутренняя энергия из (1.4) U=iRT/2, тогда CV= iR/2.

 Получите свидетельство
Получите свидетельство Вход
Вход


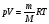
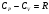 .
.








 Законы термодинамики (29.59 KB)
Законы термодинамики (29.59 KB)
 0
0 523
523 0
0 Нравится
0
Нравится
0





