Дано:
АВС – прямоугольный треугольник, ∠С - прямой, Е ∈ АВ, К ∈ АС, АК = 4 см, КС = 8 см, ЕК= 1*2/3 см, ∠K - прямой. АС = в, ВС = а, АВ = с.
Найти:
1) АВ, ВС, ∠A ;∠B.
2) площадь S △ABC;
3) периметр Р △ABC;
4) биссектрису ВМ;

5) медиану СТ;
6) высоту СХ;
7) длину окружности вписанной в △AEK;
8) площадь круга, описанного около △AKE.
Решение:
△AEK ~ △ABC (∠С = ∠K, ∠K - общий), значит, AK/AC = EK/BC = 4/12; 5/3 : BC = 1:3;
BC = 5.
По теореме Пифагора АС2 + ВС2 = АВ2;
АВ2= 144 + 25=169;
АВ =13 см.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



 В
В 

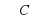 - прямой . Е Е
- прямой . Е Е АВ, К
АВ, К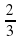 см,
см,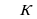 - прямой . АС=в, ВС=а, АВ=с
- прямой . АС=в, ВС=а, АВ=с 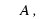
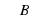 ;
;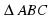 ;
;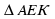 ;
;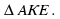
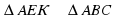 (
(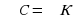 , ,
, ,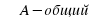 ), значит,
), значит, 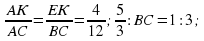
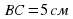 .
.








 Задачи по математике "Прямоугольный треугольник" (22.21 КB)
Задачи по математике "Прямоугольный треугольник" (22.21 КB)
 0
0 406
406 28
28 Нравится
0
Нравится
0






