Метрические соотношения в окружности. Разбор типовых задач.
Задачи по геометрии традиционно считаются «страшными» и «нелюбимыми» для значительного количества учащихся. Это объясняется и сложностью самого предмета геометрии, и большим объёмом изучаемого материала, и ограниченностью по времени при его изложении на уроках. Вместе с тем, именно планиметрия очень хорошо развивает мышление учащихся.
В рамках статьи мы рассмотрим задачи на окружность по теме«Метрические соотношения в окружности». К теме предлагаются:
- теоретическая справка;
- примеры решения задач (разбираются основные геометрические конструкции и подходы);
- задачи для самостоятельного решения (с ответами).
Метрические соотношения в окружности
| 1 |
СА = СВ | Отрезки касательных к окружности, проведенные из одной точки, равны. |
| 2 |
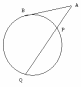
| Если через точку А проведены касательная АВ и секущая, которая пересекает окружность в точках Р и Q, то |
| 3 |
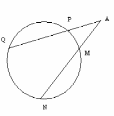
| Если через точку А, лежащую вне окружности проведены две секущие, одна из которых пересекает окружность в точках M, N, другая - в точках P, Q, то |
| 4 |
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Примеры решения задач.
Пример 1.
В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 2 см, 4 см, 6 см. Определить вид треугольника.
Решение.
П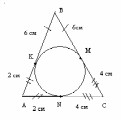 усть окружность вписана в треугольник АВС и касается его сторон в точках K, M и N. По свойству отрезков касательных AK=KN=2 см, СM=CN=4 см, BK=BM =6см. Тогда АВ=8 см, АС= 6 см, ВС=10 см. Т.к. 10
усть окружность вписана в треугольник АВС и касается его сторон в точках K, M и N. По свойству отрезков касательных AK=KN=2 см, СM=CN=4 см, BK=BM =6см. Тогда АВ=8 см, АС= 6 см, ВС=10 см. Т.к. 10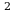 = 8
= 8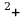 6
6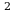 , то
, то 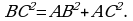 Следовательно, треугольник АВС прямоугольный с прямым углом А.
Следовательно, треугольник АВС прямоугольный с прямым углом А.
Ответ: прямоугольный.
Пример 2.
Катеты прямоугольного треугольника 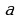 и
и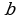 , гипотенуза
, гипотенуза 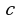 . Вычислить радиус
. Вычислить радиус 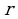 вписанной в треугольник окружности.
вписанной в треугольник окружности.
Р ешение.
ешение.
Пусть 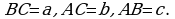 Из центра О вписанной в треугольник АВС окружности проведем радиусы ОF, OE, OD в точки ее касания со сторонами АВ, АС, ВС соответственно. Тогда
Из центра О вписанной в треугольник АВС окружности проведем радиусы ОF, OE, OD в точки ее касания со сторонами АВ, АС, ВС соответственно. Тогда 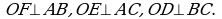
Посвойству отрезков касательных 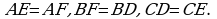 EODC – квадрат, OE = OD = CD = CE = r. Отсюда
EODC – квадрат, OE = OD = CD = CE = r. Отсюда 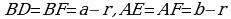 .Т.к.
.Т.к. 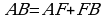 , то получаем
, то получаем 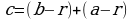 , а искомый радиус
, а искомый радиус 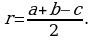
Ответ: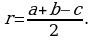
Пример 3.
В треугольник со сторонами 6 см, 10 см и 12 см вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найти периметр отсеченного треугольника.
треугольник со сторонами 6 см, 10 см и 12 см вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найти периметр отсеченного треугольника.
Решение.
Пусть ВС=6 см, АС= 10 см, АВ=12 см. Заметим, что С – тупой угол, т.к. 12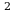 6
6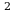 + 10
+ 10 . Проведем касательную к окружности, пересекающую две большие стороны треугольника в точках Xи Y, и обозначим точки касания М, N, P и К. Учитывая равенство пар отрезков касательных, проведенных к окружности из точек X и Y, заметим, что
. Проведем касательную к окружности, пересекающую две большие стороны треугольника в точках Xи Y, и обозначим точки касания М, N, P и К. Учитывая равенство пар отрезков касательных, проведенных к окружности из точек X и Y, заметим, что 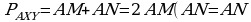 и
и
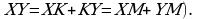 Но
Но 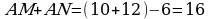 (см), потому, что
(см), потому, что 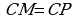 и
и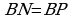 , а
, а  см.
см.
Ответ: 16 см.
Пример 4.
С торона ВС треугольника АВС равна 2 см. Окружность проходит через точки А и В, причем касается стороны ВС в точке В и пересекает сторону АС в точке М. Чему равна длина стороны АС, если известно, что АМ = СМ+ВС?
торона ВС треугольника АВС равна 2 см. Окружность проходит через точки А и В, причем касается стороны ВС в точке В и пересекает сторону АС в точке М. Чему равна длина стороны АС, если известно, что АМ = СМ+ВС?
Решение.
Обозначим через х длину отрезка СМ, тогда АМ = 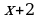 , АС = 2х + 2. По теореме о касательной и секущей
, АС = 2х + 2. По теореме о касательной и секущей 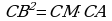 , т.е.
, т.е. 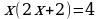 . Из этого уравнения находим: х=1. Значит, АС = 4 см.
. Из этого уравнения находим: х=1. Значит, АС = 4 см.
Ответ:4 см.
Пример 5.
С торона АВ квадрата АВСD равна 1 и является хордой некоторой окружности, причем все остальные стороны квадрата лежат вне этой окружности. Длина касательной СК, проведенной из вершины С к этой же окружности, равна 2. Чему равен диаметр этой окружности?
торона АВ квадрата АВСD равна 1 и является хордой некоторой окружности, причем все остальные стороны квадрата лежат вне этой окружности. Длина касательной СК, проведенной из вершины С к этой же окружности, равна 2. Чему равен диаметр этой окружности?
Решение.
Продолжив сторону квадрата СВ до пересечения с окружностью , получим треугольник АВL. Так как угол АВL прямой, то АL- диаметр.
По теореме о касательной и секущей 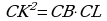 . Отсюда ВL = 3.
. Отсюда ВL = 3.
По теореме Пифагора 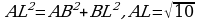 .
.
Ответ: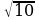 .
.
Пример 6.
Окружность радиусаRпроходит через вершину А равнобедренного треугольника АВС, касается основания ВС в точке В и пересекает сторону АС в точке D. Найдите длину боковой стороны, если DC = 3 АD.
Решение.
О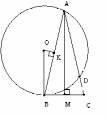 кружность касается прямой ВС в точке В. Следовательно, центр окружности – точка О – лежит на перпендикуляре, восстановленном к ВС в точке В. С другой стороны, центр окружности лежит на серединном перпендикуляре отрезка АВ, т.е. АК=КВ. Обозначим через b длину стороны АВ, а через
кружность касается прямой ВС в точке В. Следовательно, центр окружности – точка О – лежит на перпендикуляре, восстановленном к ВС в точке В. С другой стороны, центр окружности лежит на серединном перпендикуляре отрезка АВ, т.е. АК=КВ. Обозначим через b длину стороны АВ, а через 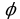 угол ВОК. Из
угол ВОК. Из 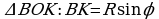 , тогда
, тогда 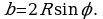 (1) Так как
(1) Так как 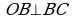 и
и 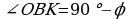 , то
, то 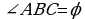 . Если М – середина ВС, то
. Если М – середина ВС, то 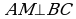 и
и 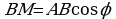 , значит
, значит 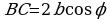 . (2)По условию
. (2)По условию 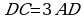 , поэтому
, поэтому 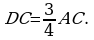 По теореме о касательной и секущей
По теореме о касательной и секущей 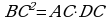 , т.е.
, т.е.  Отсюда, учитывая (2), получим
Отсюда, учитывая (2), получим 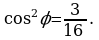 Теперь из (1) находим
Теперь из (1) находим 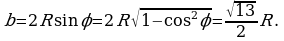
Ответ: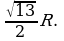
Пример 7.
Окружность, проходящая через вершину А треугольника АВС, касается стороны ВС в точке М и пересекает стороны АС и АВ в точках L иK, отличных от вершины А. Найдите отношение АС : АВ, если известно, что длина отрезка LC в два раза больше длины отрезка КВ, а отношение СМ : ВМ = 3 : 2.
Решение.
И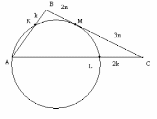 з условия следует, что из точек В и С к окружности проведены касательная (М – точка касания) и секущие СА и ВА; что ВК = k, CL = 2k, BM = 2n, MC = 3n, где n0, m0.
з условия следует, что из точек В и С к окружности проведены касательная (М – точка касания) и секущие СА и ВА; что ВК = k, CL = 2k, BM = 2n, MC = 3n, где n0, m0.
По теореме о касательной и секущей имеем
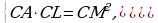
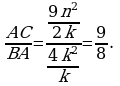
Ответ: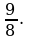
Пример 8.
И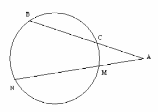 з точки вне круга проведены две секущие. Внутренний отрезок первой равен 47, а внешний 9, внутренний отрезок второй секущей на 72 больше внешнего ее отрезка. Определите длину второй секущей.
з точки вне круга проведены две секущие. Внутренний отрезок первой равен 47, а внешний 9, внутренний отрезок второй секущей на 72 больше внешнего ее отрезка. Определите длину второй секущей.
Решение.
Пусть из точки А проведены секущие, пересекающие окружность соответственно в точках В и С, M и N. Тогда ВС = 47, АС = 9. Обозначим длину отрезка АМ через х, тогда МN = x + 72. Используя то, что 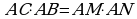 получим уравнение
получим уравнение 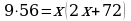 . Из которого х=6. Тогда АN = 84.
. Из которого х=6. Тогда АN = 84.
Ответ:84.
Пример 9.
На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М и боковую сторону ВС в точке N. Найдите длины отрезков МN и NС, если АС = а и АВ = b.
Решение.
Т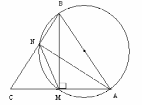 ак как АВ – диаметр окружности, то
ак как АВ – диаметр окружности, то 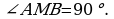
Тогда ВМ – высота равнобедренного треугольника АВС. Отсюда АМ=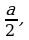
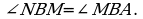 Следовательно,
Следовательно, 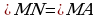 и
и 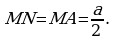
Имеем 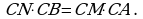 Отсюда
Отсюда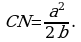
Ответ: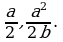
Пример 10.
Окружность, пересекающая боковые стороны АС и СВ равнобедренного треугольника АСВ соответственно в точках Р и Q, является описанной около треугольника АВQ. Отрезки АQ и ВР пересекаются в точке D так, что АQ: AD = 4:3. Найдите площадь треугольника DQВ, если площадь треугольника РQС равна 3.
Решение.
Так как СА и СВ секущие и АС = ВС как боковые стороны равнобедренного треугольника АСВ, то из соотношения 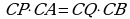 следует, что СР = СQ, и значит, АРQВ –равнобедренная трапеция.
следует, что СР = СQ, и значит, АРQВ –равнобедренная трапеция.
Т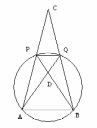 реугольники РDQ и ВDА подобны по двум углам и так как по условию АQ: AD = 4:3, то РQ:АВ = 1:3.
реугольники РDQ и ВDА подобны по двум углам и так как по условию АQ: AD = 4:3, то РQ:АВ = 1:3.
Из подобия треугольников СРQ и САВ следует, что  Если обозначить S
Если обозначить S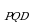 через x,
через x,
то 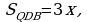
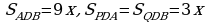 ,
,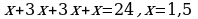 ,
, 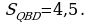
Ответ: 4,5.
Пример 11.
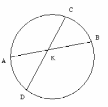
Расстояние от точки Р до центра окружности радиуса 11 равно 7. Через точку Р проведена хорда, равная 18. Найдите отрезки, на которые делится хорда точкой Р.
Решение.
П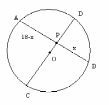 усть О – центр окружности, АВ – данная хорда. Проведем диаметр СD, содержащий точку Р (Р лежит между О и D). Обозначим через х длину отрезка РВ, тогда АР = 18 – х, DР = ОD – ОР = 11- 7 = 4, РС = ОР + ОС = 7+11 = 18.
усть О – центр окружности, АВ – данная хорда. Проведем диаметр СD, содержащий точку Р (Р лежит между О и D). Обозначим через х длину отрезка РВ, тогда АР = 18 – х, DР = ОD – ОР = 11- 7 = 4, РС = ОР + ОС = 7+11 = 18.
По теореме о пересекающихся хордах 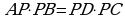
 , или
, или 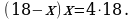 Из этого уравнения получаем, что х=12 или х=6.
Из этого уравнения получаем, что х=12 или х=6.
Значит, хорда АВ делится точкой Р на отрезки 12 и 6.
Ответ:12 и 6.
Пример 12.
С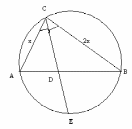 торона АВ треугольника АВС равна 3, ВС = 2АС, Е – точка пересечения продолжения биссектрисы СD данного треугольника с описанной около него окружностью, DE= 1. Найдите сторону АС.
торона АВ треугольника АВС равна 3, ВС = 2АС, Е – точка пересечения продолжения биссектрисы СD данного треугольника с описанной около него окружностью, DE= 1. Найдите сторону АС.
Решение.
По свойству биссектрисы треугольника АВС имеем  и, поскольку
и, поскольку 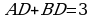 , то
, то 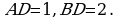
По теореме о пересекающихся хордах  . Отсюда
. Отсюда 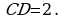
По свойству биссектрисы, обозначив 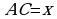 , получаем
, получаем 
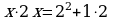 ,
, 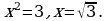
Ответ: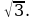
Пример 13.
Найдите синус угла между двумя хордами, если точка их пересечения удалена от центра окружности на 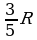 и делит одну из хорд в отношении 4:9.
и делит одну из хорд в отношении 4:9.
Решение.
Пусть АВ и СD данные хорды, Р – точка их пересечения. Тогда ОР =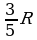 и СР : РD = 4:9.
и СР : РD = 4:9.
Так как ОА = ОВ = R, то ∆АОВ равнобедренный с основанием АВ и 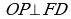 , АР = РВ.
, АР = РВ.
П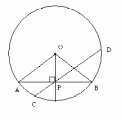 о теореме Пифагора
о теореме Пифагора 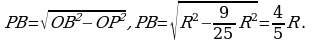
По теореме о произведении отрезков пересекающихся хорд 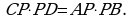
Если СР = 4х, а РD = 9х, то получим уравнение 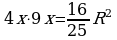 , откуда
, откуда 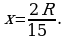
Следовательно, 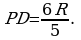
Из треугольника ОРD по теореме косинусов 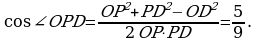 Так как
Так как 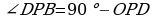 , то
, то 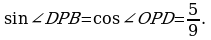
Ответ: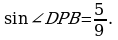
Задачи для самостоятельного решения.
1. В треугольник АВС вписана окружность, которая касается стороны АВ в точке С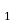 , стороны ВС в точке А
, стороны ВС в точке А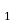 , стороны СА в точке В
, стороны СА в точке В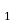 . Найдите периметр треугольника, если АС
. Найдите периметр треугольника, если АС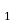 =3, ВА
=3, ВА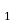 =5, СВ
=5, СВ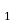 =2.
=2.
2. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 см и 12 см. Найдите катеты треугольника.
3.В равнобедренный треугольник с основанием 12 см вписана окружность, и к ней проведены три касательных так, что они отсекают от данного треугольника три малых треугольника. Сумма периметров малых треугольников равна 48 см. Найдите боковую сторону данного треугольника.
4. Радиус окружности равен r. Из точки М проведена секущая МВ, проходящая через центр окружности, и касательная МА, причем МВ = 2 МА. Найти на каком расстоянии от центра окружности находится точка М.
5. В прямоугольном треугольнике АВС с катетами АВ = 4 и ВС = 4 через середины сторон АВ и АС проведена окружность, касающаяся стороны ВС. Найдите длину отрезка гипотенузы АС, который лежит внутри этой окружности.
6.Окружность, проходящая через вершину Р треугольника PQR, касается стороны QR в точке F и пересекает стороны PQ и PR соответственно в точках М и N, отличных от вершины Р. Найдите отношение QF : FR, если известно, что длина стороны PQ в 1,5 раза больше длины стороны PR, а отношение QM : RN = 1: 6.
7. Из точки А, взятой вне круга, проведены две секущие АВС и АDЕ (АВ и АD –внешние отрезки секущих) и хорды ВD и ЕС. Докажите, что ∆АВD ~ ∆АСЕ.
8.Из точки А проведены два луча, пересекающие данную окружность: один - в точках В и С, другой – в точках D и Е. Известно, что АВ = 7, ВС = 7, АD = 10. Найдите DЕ.
9.Из точки В к окружности с центром О проведена касательная. Прямая, проходящая через точку касания М, пересекает окружность также в точке N , и отрезок ОВ – в точке А вне окружности. Найти радиус окружности, если ОВ = 8, МN = 1, а угол МАО равен удвоенному углу МВО.
10.Точка М внутри окружности делит хорду этой окружности на отрезки, равные а и b. Через точку М проведена хорда АВ, делящаяся точкой М пополам. Найдите АВ.
11.Найти радиус круга, в сегмент которого, соответствующий хорде длиной 6 см, вписан квадрат со стороной 2 см.
12.Середина полуокружности соединена с концами диаметра и через середины соединяющих отрезков проведена хорда. Каждый из боковых отрезков хорды равен с. Найдите радиус окружности.
Ответы и указания.
1. 20 см
2. 8 см и 15 см
3. 18 см
4.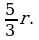
5.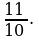
6.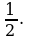
8. 0,5
9. 2
10. 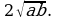
11. 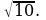
12. с(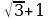 ).
).

 Получите свидетельство
Получите свидетельство Вход
Вход


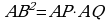 .
.
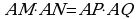
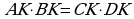









 Задачи на окружность. 9 класс. (366.53 KB)
Задачи на окружность. 9 класс. (366.53 KB)
 0
0 3902
3902 190
190 Нравится
0
Нравится
0





