План-конспект занятия №1.
Тема занятия: «Задачи на движение в одном направлении».
Цель занятия:
формирование учебно-познавательной компетенции:
обобщить теоретический материал по теме «Задачи на движение в одном направлении», рассмотреть решения типичных задач;
формирование математической компетенции:
использовать приобретенные знания и умения в практической деятельности и повседневной жизни;
формирование оценочной компетенции:
развивать умение оценивать свой уровень знаний и стремление его повышать.
1 этап занятия (3 минуты) – организационный момент.
Учитель сообщает тему занятия, его цель, структуру, необходимость проведения занятия. На экране появляются слайды №1,2.
2 этап занятия (6 минут) - повторение основных теоретических знаний.
При повторении используется презентация, которая сопровождается речью учителя. Каждый новый объект слайда выводится по щелчку.
Учитель: При решении большинства задач очень удобно использовать представление данных задачи и дальнейших рассуждений в виде таблицы. (На экране слайд №3.1). Для экономии времени в задачах на движение используются обозначения скорости (V), времени (t) и расстояния(S). Как найти одну из этих величин, зная две другие? (На экране слайд №3.2). Как перевести минуты в часы? (На экране слайд №3.3). Как перевести км/ч в м/мин и наоборот? (На экране слайд №3.4). Выучить все формулы невозможно, поэтому нужно понимать, почему именно таким образом происходит перевод одних единиц в другие. Например, если за 1 час автомобиль проезжает Vкм, метров – в 1000 раз больше, а за 1минуту – в 60 раз меньше.
Учащиеся записывают формулы в тетрадь.
3 этап занятия (40 минут) – решение типичных задач.
Учитель: Рассмотрим одну из задач на движение в одном направлении.(На экране слайд №4). Давайте прочитаем задачу… А теперь составим табличку, соответствующую условию задачи. (На экране слайд №5.1). Обозначим скорость Ι автомобиля через х, тогда скорость ΙΙ автомобиля 24 и х+16. Небольшая подсказка: если это не сильно усложняет решение задачи, желательно через х обозначать именно ту величину, которую придется записывать в ответ, чтобы второпях не ошибиться. (На экране слайды №5.2, 5.3). Заполним строчки таблицы, соответствующие расстоянию и времени. (На экране слайды5.4, 5.5). Получили дробно-рациональное уравнение. Важно помнить, что его знаменатель должен быть не равен нулю! (На экране слайд №5.6). После преобразований получаем квадратное уравнение (на экране слайды №5.7, 5.8), которое решаем с помощью формул. Чтобы не тратить «мозговые клеточки» на громоздкие вычисления, используем распределительное свойство умножения относительно сложения и свойство квадратного корня. (На экране слайд №5.9, 5.10). По смыслу задачи корень уравнения не может быть отрицательным. Значит, решая тесты, в целях экономии времени можно не высчитывать отрицательный корень. Заметив, что корень удовлетворяет условию 2∙24∙(х+16)≠0, записываем его в ответ. Ответ: 32.
Задача 2, приведенная на слайде №6, отличается от предыдущей только тем, что указаны ограничения скорости первого автомобиля. Поэтому, если навыки решения задач у учащихся развиты слабо, то можно полностью решить эту задачу. В сильном же классе достаточно пояснить учащимся, что ограничение скорости дано в задаче потому, что в квадратном уравнении получается 2 положительных корня. (Ответ: 52.)
Учитель: Рассмотрим задачу 3 (на экране слайд №7). Что означает фраза «за час автомобилист проезжает на 40 км больше, чем велосипедист»? Правильно, речь идет о скорости. Опять составим таблицу, соответствующую условию задачи, которая поможет нам составить уравнение для решения задачи.
Учитель вызывает к доске учащегося, который на доске заполняет таблицу:
автомобилист велосипедист
V(км/ч) х + 40 х
t (ч) 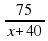 + 6 =
+ 6 = 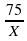
S (км) 75 75 Ответ: 10.
Если учащиеся успешно справляются с решением дробно-рациональных уравнений, то, в целях экономии времени, достаточно составить уравнение, не решая его.
Учитель: Следующая задача 4 (на экране слайд №8).
Учащиеся читают задачу и один из них опять на доске составляет таблицу и уравнение для решения задачи:
туда обратно
V(км/ч) х - 3 х
t (ч)  =
=  + 3
+ 3
S (км) 70 70 Ответ: 10.
Учитель: Рассмотрим задачу 5 (на экране слайд №9). При составлении уравнения обратите внимание на то, что скорость Ι велосипедиста больше, значит, время его меньше. Чтобы приравнять две величины, необходимо к меньшему прибавить разницу во времени! Первым пришел к финишу тот велосипедист, скорость которого больше, то есть Ι, значит его скорость и обозначаем через х (корень уравнения сразу идет в ответ, не нужно дополнительных действий).
С помощью учащегося получаем таблицу и уравнение:
Ι ΙΙ
V(км/ч) х х - 1
t (ч) 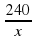 + 1 =
+ 1 = 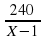
S (км) 240 240 Ответ: 16.
Учитель: Обратите внимание на задачу 6 (на экране слайд №10). Чем она отличается от предыдущей? Найти скорость велосипедиста, пришедшего к финишу вторым! Значит, его скорость обозначаем через х, и его время будет больше! Задача решается аналогично.
(Необходимость решения вновь зависит от состава учащихся). Ответ: 8.
Учитель: Не всегда для решения задачи достаточно одного уравнения. Задачу 7 (на экране слайд №11) мы попробуем решить с помощью системы уравнений. Так как скорость автомобиля не известна, то обозначим ее через х, а расстояние от А до С – через у, 30 мин =  Получим следующие таблицы (так как задача сложнее предыдущих, их заполняет учитель):
Получим следующие таблицы (так как задача сложнее предыдущих, их заполняет учитель):
автомобиль мотоциклист автомобиль мотоциклист
V(км/ч) х 90 х 90
t (ч) 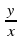 -
-  =
= 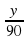
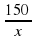 =
= 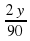 +
+ 
S (км) у у 150 2у
Получим систему уравнений: Решим ее, умножив первое уравнение системы на -2 и сложив со вторым:
Решим ее, умножив первое уравнение системы на -2 и сложив со вторым: 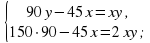

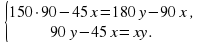
Из первого уравнения х = 4у – 300. Подставив значение х во второе уравнение и преобразовав, получим квадратное уравнение 4у² - 210у – 13500 = 0. Используя вторую формулу для нахождении дискриминанта, получим
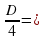 105² + 4∙13500 = 15² ∙ 7² + 4 ∙ 15 ∙ 15 ∙ 60 = 15² ∙ (49 + 240) = 15² ∙ 17²;
105² + 4∙13500 = 15² ∙ 7² + 4 ∙ 15 ∙ 15 ∙ 60 = 15² ∙ (49 + 240) = 15² ∙ 17²;
 . Так как у 0, то у = 90. Ответ: 90.
. Так как у 0, то у = 90. Ответ: 90.
Обратите внимание на то, что и в этой задаче мы использовали разложение на множители для упрощения вычислений.
Задачу 7 нет необходимости решать со слабыми учащимися, так как непростые вычисления не прибавят им уверенности в своих силах.
Учитель: Рассмотрим задачу 8 (на экране слайд №12). Прежде, чем приступать к решению задачи, обратим внимание на единицы измерения и переведем км/ч в м/мин: 1,5 км/ч = 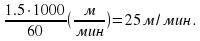 Если решать задачу, используя таблицу то получим:
Если решать задачу, используя таблицу то получим:
Ι ΙΙ
V(км/ч) х + 25 х
t (ч) t t
S (км) (x + 25)t - xt = 300 Отсюда t = 12 мин.
Для уверенности в том, что задача решена верно, всегда не помешает второй способ решения. Если вдуматься в условие задачи, то становится понятным, что 25 м/мин – это скорость удаления пешеходов друг от друга. Так как расстояние между ними должно стать 300м, то t = 300 : 25 = 12. Этот способ более прост.
Учитель: С учетом только что решенной задачи, следующая задача 9 не должна показаться сложной (на экране слайд №13). Так как мотоциклисты находятся в точках окружности, принадлежащих одному диаметру, то расстояние между ними 14 : 2 = 7 (км). Скорость сближения 21 км/ч. Тогда время сближения 7 : 21 = 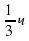 = 20 мин. Ответ: 20.
= 20 мин. Ответ: 20.
Учитель: Задачу 10 тоже можно решить двумя способами (на экране слайд №14). Обозначив через х время, которое был в пути второй турист, и используя таблицу, составим уравнение для решения задачи.
Ι ΙΙ
V(км/ч) 16 16 16 56
t (ч) 1,5 1,5 1 х х
S (км) 16 ∙ 1,5 + 16 + 16х = 56х
40х = 40, х = 1. Значит, второй турист был в пути 1 ч и проехал 56 км. Ответ: 56.
С более сильными учащимися можно решить и задачу 11 (на экране слайд №15). Учитель показывает решение задачи сам либо вызывает сильного учащегося к доске.
Учитель: В следующей задаче 11 в движении участвуют три велосипедиста. 2ч 20мин = 2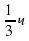 =
=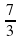 ч. В условии обозначены два момента: третий велосипедист догоняет второго и третий догоняет первого. Значит, обозначив через х скорость ΙΙΙ и через t время с момента выезда ΙΙ велосипедиста, через которое ΙΙΙ догонит ΙΙ, составим таблицы:
ч. В условии обозначены два момента: третий велосипедист догоняет второго и третий догоняет первого. Значит, обозначив через х скорость ΙΙΙ и через t время с момента выезда ΙΙ велосипедиста, через которое ΙΙΙ догонит ΙΙ, составим таблицы:
ΙΙ ΙΙΙ Ι ΙΙΙ
V(км/ч) 10 х 15 x
t (ч)  t t-1 1 + t +
t t-1 1 + t + 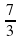 t – 1 +
t – 1 + 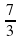
S (км) 10t = x(t-1) 15 ∙ (t +  ) = x(t +
) = x(t +  )
)
Получим систему уравнений: Вычтем из первого уравнения второе и выразим из первого уравнения х. Получим:
Подставив х во второе уравнение и преобразовав, получим квадратное уравнение 3t² + 13t – 30 = 0, положительный корень которого t =  . Тогда х = 25. Ответ: 25.
. Тогда х = 25. Ответ: 25.
Учитель: Прочитав следующую задачу (на экране слайд №16), с чего начнем решение? Да, с перевода м/мин в км/ч. 750м/мин =  (км/ч) = 45км/ч. Теперь табличка и уравнение:
(км/ч) = 45км/ч. Теперь табличка и уравнение:
товарный скорый
V(км/ч) х х + 45
t (ч)  =
=  + 2
+ 2
S (км) 180 180 Ответ: 45.
Учитель: Следующие две задачи - на движение по кругу. Рассмотрим первую из них (на экране слайд №17). Обозначив скорость второго автомобиля через х и, учитывая, что 40мин =  ч, получим таблицу и уравнение:
ч, получим таблицу и уравнение:
Ι ΙΙ
V(км/ч) 80 х
t (ч) 

S (км) 80 ∙  -
-  x = 14 Ответ: 59.
x = 14 Ответ: 59.
Учитель: Если прочитать внимательно задачу 14 (на экране слайд №18), то мы видим, что до первой встречи мотоциклист был в пути 10 мин =  , а велосипедист – 40 мин =
, а велосипедист – 40 мин =  ч. Значит, одно и то же расстояние велосипедист проезжает в 4 раза дольше. Поэтому, если скорость мотоциклиста обозначить через х, то скорость велосипедиста будет
ч. Значит, одно и то же расстояние велосипедист проезжает в 4 раза дольше. Поэтому, если скорость мотоциклиста обозначить через х, то скорость велосипедиста будет  Составим таблицу и уравнение для решения задачи (к доске выходит один из учащихся):
Составим таблицу и уравнение для решения задачи (к доске выходит один из учащихся):
велосипедист мотоциклист
V(км/ч)  х х
х х
t (ч) 

S (км)  ∙
∙  х + 30 =
х + 30 =  х х = 80 Ответ: 80.
х х = 80 Ответ: 80.
4 этап занятия (25 минут) – самостоятельная работа.
Учащиеся выполняют самостоятельную работу по вариантам. Всего 6 вариантов. Учитель раздает карточки с заданием.
5 этап занятия (3 минуты) – проверка учащимися ответов в задачах ( на экране слайд №19 с ответами)
6 этап занятия (3 минуты) – подведение итогов.
Учитель собирает работы учащихся, оценивает устную работу учащихся на занятии. Учащиеся, проверив правильность своих ответов в задачах, могут оценить свой уровень знаний и прикладывать усилия для его повышения.
Вариант 1 (с/р №1).
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути — со скоростью 96 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 57 км/ч. Ответ дайте в км/ч. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 240 км. На следующий день он отправился обратно в А со скоростью на 1 км/ч больше прежней. По дороге он сделал остановку на 1 час. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 425 метрам? Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. |
| Вариант 2 (с/р №1). Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути - со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч. Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 154 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 150 метрам? Из одной точки круговой трассы, длина которой равна 33 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 96 км/ч, и через 45 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля.
Вариант 3 (с/р №1) . |
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 17 км/ч, а вторую половину пути - со скоростью 102 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 60 км/ч. Ответ дайте в км/ч. Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 70 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 3,5 часа позже автомобилиста. Ответ дайте в км/ч. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 77 км. На следующий день он отправился обратно в А со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 3 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 100 метрам? Из одной точки круговой трассы, длина которой равна 6 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 18 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Вариант 4 (с/р №1). |
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 9 км/ч, а вторую половину пути — со скоростью 84 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч. Ответ дайте в км/ч. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 60 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в км/ч. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 140 км. На следующий день он отправился обратно в А со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 4 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 400 метрам? Из одной точки круговой трассы, длина которой равна 34 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 107 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. |
Вариант 5 (с/р №1).
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути — со скоростью 80 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она меньше 50 км/ч. Ответ дайте в км/ч. Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 50 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 3 часа 20 минут позже автомобилиста. Ответ дайте в км/ч. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в А со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 2,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 500 метрам? Из одной точки круговой трассы, длина которой равна 6 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 120 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. Вариант 6 (с/р №1) . |
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 14 км/ч, а вторую половину пути — со скоростью 84 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 55 км/ч. Ответ дайте в км/ч. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 30 минут позже автомобилиста. Ответ дайте в км/ч. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 88 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 3 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 150 метрам? Из одной точки круговой трассы, длина которой равна 20 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 103 км/ч, и через 25 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. |

 Получите свидетельство
Получите свидетельство Вход
Вход


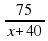 + 6 =
+ 6 = 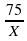
 =
=  + 3
+ 3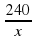 + 1 =
+ 1 = 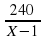
 Получим следующие таблицы (так как задача сложнее предыдущих, их заполняет учитель):
Получим следующие таблицы (так как задача сложнее предыдущих, их заполняет учитель):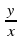 -
-  =
= 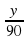
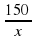 =
= 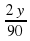 +
+  Решим ее, умножив первое уравнение системы на -2 и сложив со вторым:
Решим ее, умножив первое уравнение системы на -2 и сложив со вторым: 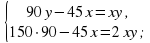

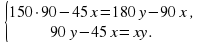
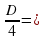 105² + 4∙13500 = 15² ∙ 7² + 4 ∙ 15 ∙ 15 ∙ 60 = 15² ∙ (49 + 240) = 15² ∙ 17²;
105² + 4∙13500 = 15² ∙ 7² + 4 ∙ 15 ∙ 15 ∙ 60 = 15² ∙ (49 + 240) = 15² ∙ 17²; . Так как у 0, то у = 90. Ответ: 90.
. Так как у 0, то у = 90. Ответ: 90.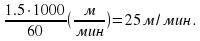 Если решать задачу, используя таблицу то получим:
Если решать задачу, используя таблицу то получим: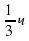 = 20 мин. Ответ: 20.
= 20 мин. Ответ: 20.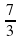 ч. В условии обозначены два момента: третий велосипедист догоняет второго и третий догоняет первого. Значит, обозначив через х скорость ΙΙΙ и через t время с момента выезда ΙΙ велосипедиста, через которое ΙΙΙ догонит ΙΙ, составим таблицы:
ч. В условии обозначены два момента: третий велосипедист догоняет второго и третий догоняет первого. Значит, обозначив через х скорость ΙΙΙ и через t время с момента выезда ΙΙ велосипедиста, через которое ΙΙΙ догонит ΙΙ, составим таблицы: t t-1 1 + t +
t t-1 1 + t + 








 Задачи на движение в одном направлении (33.43 КB)
Задачи на движение в одном направлении (33.43 КB)
 0
0 669
669 42
42 Нравится
0
Нравится
0


