Взаимное расположение прямой и плоскости

Взаимное расположение прямой и плоскости

Рассмотрим плоскость  и прямую , заданную точкой  и направляющим вектором .

Существует три варианта взаимного расположения прямой и плоскости:

1) прямая пересекает плоскость в некоторой точке ;

2) прямая параллельна плоскости: ;

3) прямая лежит в плоскости: . Да, так вот нагло взяла, и лежит.

Как выяснить взаимное расположение прямой и плоскости?

Изучим аналитические условия, которые позволят нам ответить на данный вопрос. Выполним схематический чертёж, на котором прямая пересекает плоскость: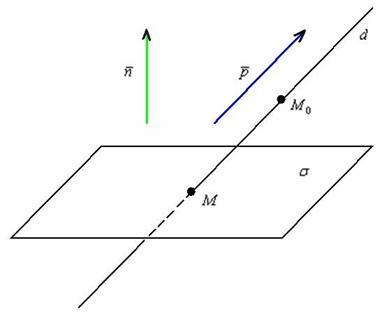

Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор  не ортогонален вектору нормали  плоскости. 

Из утверждения следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: .

В координатах условие запишется следующим образом:

Если же данные векторы ортогональны, то есть если их скалярное произведение равно нулю: , то прямая либо параллельна плоскости, либо лежит в ней: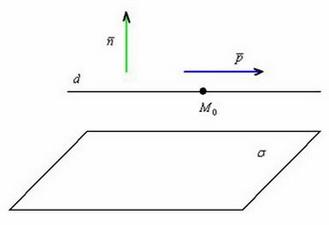

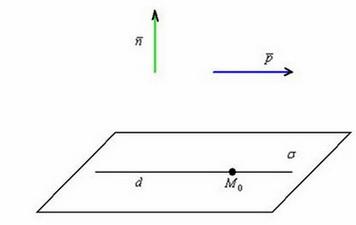
Разграничим данные случаи.

Если прямая параллельна плоскости, то точка  (а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: .

Таким образом, условие параллельности прямой и плоскости записывается следующей системой:

Если прямая лежит в плоскости, то точка  (а, значит, и ЛЮБАЯ точка данной прямой) удовлетворяет уравнению плоскости: .

Аналитические условия данного случая запишутся похожей системой:

Разборки с взаимным расположением прямой и плоскости достаточно примитивны – всего в два шага. Кроме того, на практике можно обойтись даже без всяких систем

Пример 1

Выяснить взаимное расположение прямой, заданной точкой  и направляющим вектором , и плоскости .

Решение: Вытащим вектор нормали плоскости: .

Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: , значит, прямая либо параллельна плоскости, либо лежит в ней.

Подставим координаты точки  в уравнение плоскости:

Получено верное равенство, следовательно, точка  лежит в данной плоскости. Разумеется, и любая точка прямой тоже будет принадлежать плоскости.

Ответ: прямая лежит в плоскости

Пример 2

Выяснить взаимное расположение плоскости  и прямой .

Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.

После небольшой разминки мускулатуры начинаем накидывать блины на штангу:

Основные задачи на прямую и плоскость

Рассмотрим прямую , которая пересекает плоскость . Требуется найти точку, в которой прямая пересекает плоскость: .

Пример 3

Дана прямая  и плоскость . Требуется:

а) доказать, что прямая пересекает плоскость;

б) найти точку пересечения прямой и плоскости;

в) через прямую  провести плоскость  («омега»), перпендикулярную плоскости ;

г) найти проекцию прямой  на плоскость ;

д) найти угол между прямой  и плоскостью .

Решение:

а) Из уравнений прямой находим принадлежащую ей точку и направляющий вектор:

Вектор нормали плоскости, как всегда, сдаётся без боя:

Вычислим скалярное произведение:
, значит, прямая пересекает плоскость, что и требовалось доказать.

Как найти точку пересечения прямой и плоскости?

б) Найдём точку пересечения плоскости и прямой: . Не «Чёрный квадрат» Малевича, но тоже шедевр:

Сначала перепишем уравнения прямой в параметрической форме:

Точка  принадлежит данной прямой, поэтому её координаты  при некотором значении параметра  удовлетворяют параметрическим уравнениям:
, или одной строчкой: .

С другой стороны, точка  принадлежит и плоскости , следовательно, координаты точки должны удовлетворять уравнению плоскости , то есть должно выполняться равенство:

 – ну, или попросту параметрические координаты точки нужно подставить в уравнение плоскости.

Раскрываем скобки, приводим подобные слагаемые и находим «тэ нулевое»:

 – полученное значение параметра подставляем в параметрические выражения координат нашей точки:

Интересно, что в данном пункте всё обошлось даже без векторов.

Чистка хвоста очевидна: координаты точки  должны «подходить» и в уравнения прямой и в уравнение плоскости. Проверку несложно выполнить устно.

в) Найдём уравнение плоскости , которая перпендикулярна плоскости  и проходит через прямую . Выполним схематический чертёж:

Уравнение плоскости  можно составить по любой точке, которая принадлежит прямой , направляющему вектору  прямой  и вектору нормали  плоскости .

В качестве точки, принадлежащей прямой «дэ», не возбраняется, конечно, взять найденную в предыдущем пункте точку пересечения , но в произвольной практической задаче она чаще всего не известна. Поэтому обычно используют самую «лёгкую добычу». В данном случае, очевидно, точку:
.

Уравнение плоскости «омега» составим по точке  и двум неколлинеарным векторам :

Таким образом: 

Проверка опять же довольно простая. Устно находим скалярное произведение нормальных векторов  двух плоскостей. Оно равно нулю, значит, плоскости перпендикулярны. На втором шаге необходимо убедиться, что прямая «дэ» действительно лежит в найденной плоскости «омега». Можно использовать типовой алгоритм, рассмотренный в самом начале урока. Но тут есть другая возможность – устно подставляем координаты двух известных точек  в полученное уравнение плоскости . Обе точки «подходят», и это гарантирует, что и вся прямая  лежит в плоскости .

Как найти уравнения проекции прямой на плоскость?

г) Что такое проекция прямой на плоскость?  

На чертеже наша «тень»  проведена малиновым цветом, а её проекция, прямая  – коричневым цветом. Легко заметить, что проекция задаётся пересечением плоскостей: , и на самом деле ответ уже готов:

Другое дело, что часто требуется представить уравнения прямой в канонической форме. Точка , принадлежащая проекции, уже известна, осталось найти её направляющий вектор:

Таким образом, канонические уравнения проекции:

Обратите внимание, что на практике для решения данной задачи, в общем-то, не надо находить именно точку пересечения  (лишняя работа). Нас устроит любая точка, принадлежащая проекции. Красавица подбирается из системы  

Есть и другой способ нахождения проекции, связанный с построением перпендикуляра к плоскости «сигма», но, я тут прикинул, он вряд ли короче. Однако на всякий случай озвучу алгоритм, вдруг понадобится кому:

– находим точку пересечения прямой и плоскости:  (вот в этом способе уже обязательно находим);
– из произвольной точки  (не совпадающей с точкой ) опускаем перпендикуляр  на плоскость  (см. следующие параграфы);
– основание перпендикуляра  находим как пересечение прямой  и плоскости ;
– составляем канонические уравнения проекции  по двум точкам: .

Как найти угол между прямой и плоскостью?

д) Логическое продолжение темы.

Если прямая  не перпендикулярна плоскости , то углом  между прямой и плоскостью называется острый угол между прямой  и её проекцией на плоскость . Если прямая перпендикулярна плоскости, то угол между ними равен 90 градусов.

Продолжим эксплуатацию геометрического инвентаря:                          

Справедлива следующая формула синуса угла между прямой и плоскостью:

Таким образом, для нахождения данной  угла достаточно знать лишь нормальный вектор плоскости и направляющий вектор прямой.

Скалярное произведение векторов уже найдено в пункте «а»: . Обратите внимание, что в формуле скалярное произведение находится под знаком модуля, который «съедает» возможный «минус».

Вычислим длины векторов:

По формуле: 

На иррациональность в знаменателе забиваем, поскольку нам нужен сам угол:

Ответ:
а) , значит, прямая пересекает плоскость;
б) ;
в) ;
г) ;
д) 

Переходим к рассмотрению частного случая – когда:

Прямая перпендикулярна плоскости

Пример 4

Дана плоскость  и точка . Требуется:

а) составить канонические уравнения прямой , проходящей через точку , перпендикулярно данной плоскости;

б) найти точку  пересечения перпендикулярной прямой и плоскости;

в) найти точку , симметричную точке  относительно плоскости .

Выполним схематический чертёж и коротко разберём алгоритм решения:

а) Как составить уравнения перпендикулярной прямой «дэ», думаю, объяснять не нужно. Подсказка есть прямо на чертеже.

б) Точка пересечения  перпендикулярной прямой и плоскости находится обычным способом (см. п. «б» предыдущего примера). К слову, точка  является проекцией прямой  на плоскость «сигма».

в) Рассмотрим отрезок . Если точка  симметрична точке  относительно плоскости, то, очевидно . По формулам деления отрезка пополам, нетрудно найти координаты нужной точки .

как составить уравнение плоскости, которая проходит через данную точку перпендикулярно данной прямой? Берём направляющий вектор прямой – он же является вектором нормали плоскости.

можно ли составить уравнение плоскости, проходящей через прямую и точку, не принадлежащую прямой? Да, конечно, причём плоскость будет определена однозначно

Все задачи на пересечение прямой и плоскости, пожалуй, исчерпаны, теперь рассмотрим что-нибудь на прямую, параллельную плоскости.

Пример 5

Даны скрещивающиеся прямые . Через прямую  провести плоскость, параллельную прямой .

Решение: Задача простая, но всё равно выполним схематический чертёж:

По условию требуется найти уравнение плоскости , которая проходит через прямую  параллельно второй прямой.

Уравнение плоскости составим по точке и двум неколлинеарным векторам.

Поскольку прямая  должна лежать в плоскости , то нам подойдёт произвольная точка , принадлежащая первой прямой, и её направляющий вектор:

С другой стороны, плоскость  должна быть параллельна прямой , а, значит, и её направляющему вектору .

Так как прямые скрещиваются, то их направляющие векторы  будут не коллинеарны.

Уравнение плоскости  составим по точке  и двум неколлинеарным векторам :

Ответ: 

Используя материалы начала урока, можно выполнить проверку – убедиться, что первая прямая действительно лежит в полученной плоскости, а вторая прямая – параллельна ей.

Аналогично можно составить уравнение плоскости , которая проходит через прямую  параллельно прямой . Решение будет точно таким же, изменится только точка – необходимо взять какую-нибудь точку, принадлежащую второй прямой. Очевидно, что данные плоскости будут параллельны: .