Получите свидетельство
Вход
- рассмотреть различные случаи взаимного расположения прямой и окружности;
- совершенствовать у учащихся навыки решения задач.
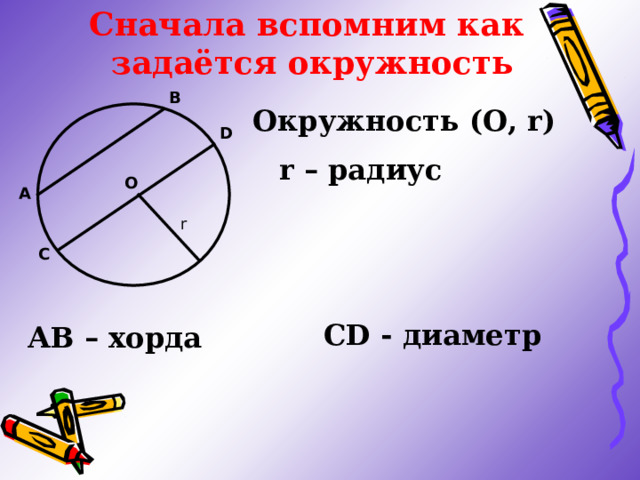
Сначала вспомним как
задаётся окружность
B
Окружность (О, r )
D
r – радиус
О
A
r
С
CD - диаметр
АВ – хорда
а
Даны окружность радиуса r и прямая а, не проходящая через центр О окружности. Расстояние от точки О до прямой а равно d .
О
r
Как вы думаете, сколько общих точек
могут иметь прямая и окружность?
1) d
A
B
H
p
d
По теореме Пифагора
O
Следовательно, точки А и В лежат на окружности и, значит, являются общими точками прямой р и данной окружности.
ВЫВОД
Если расстояние от центра окружности до прямой меньше радиуса окружности (d , то прямая и окружность имеют две общие точки.
Прямая называется секущей по отношению к окружности
2) d = r
H
М
p
ОН= r , точка Н лежит на окружности и, значит, является общей точкой прямой и окружности
d = r
O
ВЫВОД
Если расстояние от центра окружности до прямой равно радиусу окружности (d = r) , то прямая и окружность имеют одну общую точку
r М H p ОН r , поэтому для любой точки М прямой р ОМ ≥ОН r . Следовательно точка М не лежит на окружности. dr O r ВЫВОД Если расстояние от центра окружности до прямой больше радиуса окружности (dr) , то прямая и окружность не имеют общих точек " width="640"
3 ) dr
М
H
p
ОН r , поэтому для любой точки М прямой р ОМ ≥ОН r . Следовательно точка М не лежит на окружности.
dr
O
r
ВЫВОД
Если расстояние от центра окружности до прямой больше радиуса окружности (dr) , то прямая и окружность не имеют общих точек
r две общие точки одна общая точка не имеют общих точек " width="640"
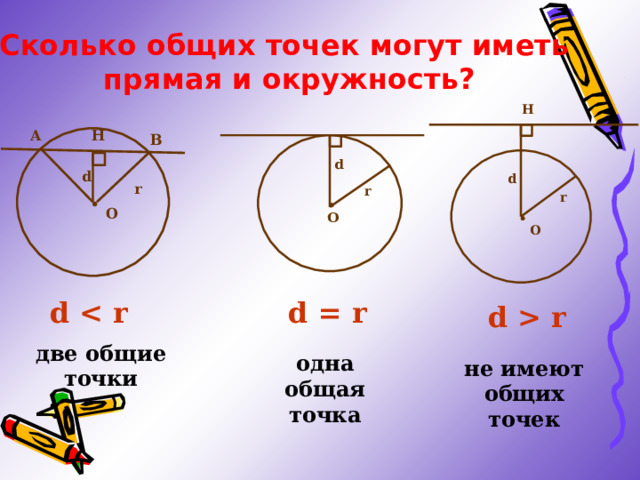
Сколько общих точек могут иметь
прямая и окружность?
d
d = r
d r
две общие точки
одна общая точка
не имеют общих точек
Взаимное расположение прямой и плоскости (165 KB)
0
317
5
Нравится
0
