Выпускная квалификационная работа магистра

84

Министерство образования и науки Российской Федерации

СТЕРЛИТАМАКСКИЙ ФИЛИАЛ

федеральноГО государственноГО бюджетноГО

образовательноГО учреждениЯ высшего образования

«Башкирский государственный университет»

Факультет педагогики и психологии

КАФЕДРА ТЕОРИИ И МЕТОДИКИ НАЧАЛЬНОГО ОБРАЗОВАНИЯ

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА магистра

Мангитбаева Людмила Владимировна

Формирование логического мышления
у младших школьников
в процессе обучения математике

e-	Выполнила:
	студентка III курса заочной формы обучения
	Направление подготовки: 44.04.01 Педагогическое образование
	Направленность: Начальное образование

e-OXz6@iGOA6

e-OXz6@iGOA6

Допущено к защите в ГЭК и проверено на объём заимствования:	e-OXz6@iGOA6
e-OXz6@iGOA6 Заведующий кафедрой к.п.н., доцент	e-OXz6@iGOA6 Руководитель д. пед. наук, профессор
_____________/ Л.Б.Абдуллина	______________/ Р.В. Канбекова
«____»____________2017 г.

e-OXz6@iGOA6

e-OXz6@iGOA6

Стерлитамак – 2017

Содержание

ВВЕДЕНИЕ	3
ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОБЛЕМЫ ЛОГИКО-МАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ МЛАДШИХ ШКОЛЬНИКОВ	10
1.1. Характеристика логического мышления младших школьников	10
1.2. Система работы по формированию логического мышления у младших школьников	24
ГЛАВА 2. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ФОРМИРОВАНИЯ ЛОГИЧЕСКИХ УМЕНИЙ У МЛАДШИХ ШКОЛЬНИКОВ	39
2.1. Организация и методики исследования	39
2.2. Результаты экспериментального исследования	63
ЗАКЛЮЧЕНИЕ СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ ПРИЛОЖЕНИЕ	72 75 80

ВВЕДЕНИЕ

Актуальность исследования определяется, во-первых, стратегией современного образования ориентированного на формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое и алгоритмическое мышление, создание условий для ее самореализации, о чем говорится в Законе РФ «Об образовании».

Во-вторых, задачами школьного математического образования, которое способствует овладению конкретными знаниями, необходимыми для ориентации в современном мире, развитию воображения и интуиции, формированию мировоззрения, формированию нравственных черт, воспитанию способности к эстетическому восприятию мира, обогащению запаса историко-научных знаний, а также формированию логического мышления.

В последние годы много говорится о необходимости нового типа образовательного результата, который ориентирован на решение реальных жизненных задач. Под этим понимается личность, которая обладает набором ключевых компетенций или общеучебных умений, а также сформированным интеллектуальным аппаратом, куда и включено формирование логического мышления. В структуре мышления выделяются следующие логические операции: сравнение, анализ, синтез, абстракция и обобщение. К процессам мышления относятся: суждение, умозаключение, определение понятий, индукция и дедукция и другие. Суждение – это высказывание, содержащее какую-либо мысль. Умозаключение представляет собой серию логически связанных высказываний, из которых выводится новое знание.

В новых федеральных государственных образовательных стандартах начального общего образования второго поколения прописано, что главной целью образовательного процесса является формирование универсальных учебных действий, таких как личностные, регулятивные, познавательные, коммуникативные. В соответствии со стандартами второго поколения, познавательные универсальные действия включают: общеучебные, логические, а также постановку и решение проблемы.

В настоящее время вопрос о необходимости специальной работы учителя начальных классов над формированием логического и алгоритмического мышления у младших школьников приобретает особенное внимание по следующим причинам: во-первых, появились новые учебники для начальных классов, требующие от учащегося активной мыслительной деятельности для усвоения содержания; во-вторых, уже с начального звена школы активно внедряются факультативные курсы, для изучения которых нужно усилить логическую подготовленность учащихся начальных классов.

Существует противоречие между необходимостью формирования логического мышления у младших школьников и недостаточностью систематизированного дидактического материала, который был бы прямо направлен на его формирование в течение всего времени обучения в начальной школе. Разрешению проблемы формирования логического мышления, в течение всего времени обучения и посвящена данная выпускная квалификационная работа. Таким образом, актуальность формирования логического мышления у младших школьников на уроках математики и недостаточная реализации её на практике обусловили выбор темы исследования.

Проблемой развития логического мышления младших школьников занимались и занимаются известные ученые педагоги. М.Н. Шардаков, опубликовав в 1963 г. книгу «Мышление школьника», положил начало теоретического изучения педагогических аспектов в развитии и формировании мышления школьника. Ученые-педагоги А.В. Белошистая, Н.Б. Истомина продолжили исследование и доказали, что при обеспечении систематического педагогического воздействия на формирование логического и алгоритмического мышления, определенные интеллектуальные операции могут быть сформированы у ребенка в младшем школьном возрасте.

При этом исследования психологов В.В. Давыдова, Д. Б. Эльконина позволяют сделать вывод о том, что результативность процесса формирования и развития логического мышления в начальных классах зависит от способа организации специальной развивающей работы.

Анализ современных учебников по математике для начальной школы (учебники Н.Б. Истоминой, М.И. Моро, Л.Г. Петерсон и др.) показал, что они содержат задания, направленные на формирование логического и алгоритмического мышления у младших школьников, однако они зачастую не носят системного характера, в большинстве случаев используются в виде необязательного материала. Наиболее четко представлено внимание, логическому и алгоритмическому материалу в математике для первого класса и в математике для второго класса, в курсе Н.Б. Истоминой, однако в учебнике математики для третьего класса внимание автора значительно ослабевает.

Существует противоречие между необходимостью формирования логического и алгоритмического мышления у младших школьников и недостаточностью систематизированного дидактического материала, который был бы прямо направлен на его формирование в течение всего времени обучения в начальной школе. Разрешению проблемы формирования логического мышления у младших школьников, в течение всего времени обучения и посвящена данная выпускная квалификационная работа. Таким образом, актуальность формирования логического мышления у младших школьников на уроках математики и отсутствие реализации на практике обусловили выбор темы исследования.

Объект исследования: процесс обучения математике в начальной школе.

Предмет исследования: формирование логического мышления младших школьников в процессе обучения математике.

Цель исследования: теоретически обосновать и экспериментально проверить приемы формирования логического мышления младших школьников при обучении математике.

Гипотеза исследования: если на уроках математики реализованы следующие условия:

– систематически используются специальные задачи и задания, направленные на развитие логического мышления;

– решаются «трудные задачи» с необычным условием, в которых предоставляется возможность порассуждать;

– выполняется логическое и осознанное исследование реального мира, то уровень развития логического мышления младших школьников повысится.

Цель, объект, предмет и гипотеза исследования обусловили необходимость решения следующих задач:

– уточнить понятие «логическое мышление младших школьников» на основе изучения и анализа педагогической и методической литературы;

– описать систему работы над формированием логического мышления младших школьников на уроках математики;

– экспериментально проверить систему работы над формированием логического мышления на уроках математики.

– сформулировать рекомендации по формированию логического мышления младших школьников для учителей начальных классов.

Методологическую основу исследования составили: философские идеи теории и практики о человеке как субъекте общественных отношений; философское положение о социальной природе психологической деятельности человека, активности и ведущей роли личности в процессе ее развития и формирования; личностно-деятельностный подход в организации образовательного процесса в начальной школе; современные технологии обучения с применением информационно-коммуникативных технологий.

Для решения поставленных задач использовались теоретические и экспериментальные методы исследования.

Теоретические: анализ психолого-педагогической литературы, нормативных документов (Закон 273-ФЗ «Об образовании в Российской Федерации» 29.12.2012 г.), федеральные государственные образовательные стандарты высшего и начального общего образования (далее – ФГОС ВО и ФГОС НОО), сравнительный анализ учебных программ, учебников, учебных пособий.

Экспериментальные: наблюдение за учебно-познавательной деятельностью учащихся; наблюдение за деятельностью учителя; анкетирование; тестирование; беседа; постановка и проведение опытно-педагогического эксперимента.

Экспериментальное исследование проводилась в третьих классах на базе казённого государственного учреждения «Общеобразовательная средняя школа №10 г. Актау Республики Казахстан» в течение первого полугодия 2015-2016 года. Всего было задействовано 48 учащихся (3 «Г» и 3 «Ж» учебных классов), 2 учителя. В экспериментальном классе (3 «Г»), учителем является автор выпускной квалификационной работы. В контрольном (3 «Ж») классе, учителем является Азизова Арзу Шаваловна. Школа, где проводился эксперимент, является школой смешанного типа, т.е. обучение ведется на двух языках (русском и казахском). С 2016 года школа перешла на 12-летнее образование.

Теоретическая значимость исследования заключается в том, что его результаты дополняют имеющиеся теоретические положения о формировании логического мышления младших школьников в учебном процессе. Материалы исследования вносят определенный вклад в теорию обучения и могут служить основой для дальнейшей разработки данной проблемы.

Практическая значимость исследования состоит в том, что реализация теоретических выводов и положений работы по формированию логического мышления младших школьников позволяет совершенствовать процесс обучения математике в начальной школе. Учёт полученных результатов позволяет повысить качество обучения младших школьников на уроках математики на основе знаний учителя, о целенаправленном процессе формирования логического мышления младших школьников, а также дает возможность использования разработанных дидактических материалов в практической деятельности.

Основные положения, выдвигаемые на защиту:

1. Понятие «логическое мышление младших школьников» в образовательном процессе рассматривается нами как динамическое направленное по линии математических знаний, приобретаемое им в результате учебного взаимодействия с учителем и регулирующее его учебную деятельность, качество личности, представленное совокупностью компонентов: словесно-логическое, абстрактное (понятийное) мышление.

2. Формирование логического мышления в процессе обучения математике обеспечивается созданием следующей системы работы:

– систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на формирование логического мышления;

– решение трудных задач с «необычным» условием, в которых предоставляется младшим школьникам возможность порассуждать;

– логическое и осознанное исследование явлений реального мира.

3. Система уроков, отраженная в тематическом плане, (см. Приложение №1) представляет собой совокупность, объединенную общей целью, содержанием, организационными формами, образующими некоторую целостность.

4. Выявленные уровни сформированности логического мышления младших школьников и разработанный инструментарий диагностики (критерии) позволяют отслеживать динамику уровней и результативности формирования логического мышления у младших школьников.

Апробация и внедрение результатов исследования осуществлялась на научных студенческих конференциях СФ БашГУ (2015,2016), в опубликованных статьях «Формирование логического и алгоритмического мышления у младших школьников» в сборнике «Начальное и дошкольное образование: опыт, проблемы, перспективы: Сб. материалов IV Всероссийской научно-практической конференции, 2015 г.»; Рекомендации по реализации здоровьесберегающей функции педагога на уроках математики // Обучение в начальной школе: Республиканской метод. журн. №6 (78). 2016 г., «Развитие мышления младших школьников» в сборнике науч. трудов по материалам Всероссийской заочной научной конференции, 2016 г., представленных в списке использованной литературы.

Структура работы. Выпускная квалификационная работа состоит из введения, двух глав, заключения, списка использованных источников и литературы и приложений.

ГЛАВА 1.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ проблемы
ЛОГИКО-МАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ
МЛАДШИХ ШКОЛЬНИКОВ

1.1. Характеристика логического мышления младших школьников

Логические и психологические исследования последних лет [Пиаже, 2008, с. 34] вскрыли связь некоторых «механизмов» детского мышления с общематематическими и общелогическими понятиями.

Понятия «отношение», «структура», «законы композиции» и др., имеющие сложные математические определения, не могут быть связаны с формированием математических представлений у маленьких детей. Проще говоря, весь подлинный и отвлеченный смысл этих понятий и их место в аксиоматическом построении математики как науки есть объект усвоения уже хорошо развитой и «натренированной» в математике головы. Однако некоторые свойства вещей, являются понятными для ребенка уже сравнительно рано: на это имеются конкретные психологические данные, изложенные в трудах ученых: известные ученые педагоги и психологи отмечают, что с момента рождения до 7-10 лет у ребенка возникают и формируются сложнейшие системы общих представлений об окружающем мире и закладывается фундамент содержательно-предметного мышления. Причем на сравнительно узком эмпирическом материале дети выделяют общие схемы ориентации в пространственно-временных и причинно-следственных зависимостях вещей. Эти схемы служат своеобразным основанием той «системы координат», внутри которой ребенок начинает все глубже овладевать разными свойствами многообразного мира. Конечно, эти общие схемы мало осознаны и в малой степени могут быть выражены самим ребенком в форме отвлеченного суждения. Говоря образно, они являются интуитивной формой организации поведения ребенка (хотя, все более и более отображаются и в суждениях). Ж. Пиаже считает, что психологическое исследование развития арифметических и геометрических операций в сознании ребенка (особенно тех логических операций, которые осуществляют в них предварительные условия) позволяет точно соотнести операторные структуры мышления со структурами алгебраическими, структурами порядка и топологическими· координация двух систем действия составляет новую схему, присоединяемую к предыдущим; [Пиаже, 2008,с.43].

Исследования Ж. Пиаже показывают, прежде всего, что в период дошкольного и школьного детства у ребенка формируются такие структуры мышления, которые позволяют ему оценивать фундаментальные характеристики классов, объектов и их отношений. В период от 7 до 11 лет система отношений, основанная на принципе взаимности, приводит к образованию в сознании ребенка структуры порядка.

Рассмотрим основные положения, сформулированные Ж. Пиаже, применительно к вопросам построения учебной программы. Причем уже на стадии конкретных операций (с 7-8 лет) интеллект ребенка приобретает свойство обратимости, что исключительно важно для понимания теоретического содержания учебных предметов, в частности математики.

С одной стороны, в последние годы вопрос о необходимости специальной работы учителя начальных классов над формированием логического мышления ребенка приобретает особенную остроту по следующим причинам: во-первых, появились новые учебники для начальных классов, требующие от ученика активной мыслительной деятельности для усвоения их содержания; во-вторых, как в начальном, так и в среднем звене школы активно внедряются факультативные курсы логики, для изучения которых необходимо усилить логическую подготовку учеников младших классов. Об усилении логической подготовки говорится в методической литературе, и в объяснительных записках к учебным программам. Однако, как это делать, учитель не всегда знает. В настоящее время развитие логического мышления в значительной мере идет стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевает начальными приемами логического мышления (анализ, сравнение, синтез, абстрагирование и др.). Известный отечественный педагог В.А. Сухомлинский, в свое время значительное место уделял вопросу обучения младших школьников решению логических задач. Суть его размышлений сводится к изучению и анализу процесса решения детьми логических задач, при этом он опытным путем выявлял особенности мышления детей. Василий Александрович Сухомлинский наблюдал за ходом мышления детей на уроках, и писал, «что, прежде всего надо научить детей охватывать мысленным взором ряд предметов, явлений, событий, осмысливать связи между ними. Изучая мышление тугодумов, я все больше убеждался, что неумение осмыслить, например, задачу – следствие неумения абстрагироваться, отвлекаться от конкретного. Надо научить ребят мыслить абстрактными понятиями» [Сухомлинский, 2011 с. 124].

Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ восхождения от абстрактного к конкретному. Как показывает опыт, в младшем школьном возрасте одним из эффективных способов развития мышления является решение школьниками нестандартных логических задач. Кроме того, решение нестандартных логических задач способно привить интерес ребенка к изучению «классической» математики.

Задачи развития логического мышления младших школьников в процессе обучения математике требуют от будущего педагога логической грамотности – ему необходимы знания об особенностях математических понятий, утверждений, доказательств; он должен обладать соответствующими логическими умениями. Высокий уровень логической подготовки педагога является залогом правильной организации деятельности, которую он осуществляет при ознакомлении младших школьников с новыми понятиями, их свойствами, а также в процессе освоения программного материала.

Содержание изучаемых в начальной школе дисциплин, планируемые результаты направлены прежде всего на интеллектуальное развитие младших школьников: овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям.

Программа логико-математической подготовки младших школьников предусматривает знакомство с понятиями: каждый; какой-нибудь; один из; любой; все; не все; все, кроме; с классификацией множества предметов по заданному признаку, с определением оснований классификации. Младшие школьники знакомятся с понятием высказывания, примерами истинных и ложных высказываний, рассматривают числовые равенства и неравенства как примеры высказываний. Составляют из двух простых высказываний сложные высказывания с помощью логических связок и определяют их истинность. Учащиеся анализируют структуру составного высказывания, выделяя в нем простые высказывания, из которых оно образовано, приводят простейшие доказательства истинности или ложности данных утверждений, умеют приводить примеры, подтверждающие или опровергающие данное суждение; решают несложные комбинаторные задачи, связанные не только с необходимостью перебора возможных вариантов, но и необходимостью выполнять логические рассуждения и делать логические выводы.

Приоритетной целью современной педагогической концепции начального образования является реализация системно-деятельностного подхода, что означает владение математическими понятиями и умениями применять их в процессе обучения математике. Современный уровень обучения математике в начальной школе требует умения учащихся выполнять логические действия (операции). Так как познание – ментальный процесс, который описывается путем применения установленных логикой закономерностей, то рассмотрение проблемы внедрения системно-деятельностного подхода сквозь призму логических закономерностей составляет одну из важнейших сторон дидактики начальной школы.

Формирование научных понятий у младших школьников опирается на умения совершать логические операции и логические рассуждения.

Логическая составляющая начального математического образования связана с развитием мышления учащихся, привитием ему умений строить умозаключения, непротиворечиво давать определения понятиям, выполнять логические операции сравнения, сопоставления, доказательства.

Идея развития мышления учащихся не нова в педагогической литературе. Ещё в XVII веке английский педагог Джон Локк заметил: «Читать и писать, обучать наукам – всё это я признаю необходимым, но не главным делом… Обучать мальчика нужно, но это должно быть на втором плане, только как вспомогательное средство для развития более важных качеств» [Локк, 1988, с. 171].

В.В. Рубцов конкретизировал эти «более важные качества»: «В то же время очевидно, что место знаний, отождествляемых сегодня с информацией, умений и навыков, должны занять методы мышления, способы порождения и употребления знаний, техники понимания и рефлексии, приемы и способы коммуникации и действия. Мышление, понимание, рефлексия, коммуникация образуют деятельностный материал, из которого строятся единицы культуры и уникальности личности младшего школьника. Поэтому обозначенное нами изменение содержания практики образования является одновременно новой историко-культурной парадигмой в образовании, позволяющей образующейся личности самоопределяться в истории и культуре» [Рубцов, 2002, с. 9-10].

В данном исследовании рассматривается проблема изучения когнитивно-информационной составляющей логического содержания математической подготовки педагогов и учащихся начальной школы.

Основными принципами построения технологии обучения, направленного на формирование логических умений педагогов для начальной школы, являются: когнитивный, ориентированный на перенос знаний из математической в методическую сферу и наоборот; логический, позволяющий вскрывать сущность изучаемого материала в его связях и отношениях с другими реалиями окружающего мира; информативный, конструирующий деятельность младших школьников, связанную с решением логических задач.

Для формирования базовых позиций логического мышления у младших школьников учителю необходимо освоить: логические методы определения существенного в изучаемом объекте; алгоритм сравнения изучаемого объекта или явления; правило выполнения естественной классификации; правило достаточной доказательности рассуждений.

Для формирования логического мышления младших школьников учитель должен уметь анализировать виды доказательств с точки зрения формальной логики: «по существу», «генетические», математические и эмпирические доказательства. Доказательства «по существу» делятся на четыре главные группы (полной индукции, разделительные, опровергающие, обуславливающие), и все они применяются в математике. Генетические доказательства (доказательства по источнику происхождения) применяются в тех случаях, когда при решении вопроса об истинности утверждения нет другого пути. Этот вид доказательства способствует формированию критического мышления младших школьников.

Учитель начальных классов должен иметь представление об основах математической логики, являющейся современным этапом в развитии формальной логики, поскольку без освоения логики невозможно доказать теорему, вывести формулу, решить задачу. Теоретические сведения, которые должен усвоить учитель для формирования логического мышления младших школьников, подкрепляются примерами из начального курсов математики.

Для реализации теоретических положений, усвоенных будущими педагогами в процессе обучения в вузе в практической деятельности начальной школы необходимо выполнить анализ содержания программ по математике для начальной школы с позиции формирования логического и алгоритмического мышления. Формирование логического мышления младших школьников осуществляется при разработке схем решения задач, решении нестандартных задач, обосновании математических фактов, выполнении доказательств высказанных суждений.

Мышление совершается и развивается в единстве его содержании и форм. Благодаря многократному разу повторений, в процессе выполнений упражнений, в процессе приобретения и усвоения знаний в повседневной жизни, некоторых общих закономерностей анализа, синтеза и сравнений; абстракций, обобщения и конкретизации; индукции, дедукции и аналогии; нахождения связей и отношений; формирования понятий, их классификации и систематизации. Однако «это не значит, – пишет С.Л. Рубинштейн, – что форма независима от содержания, от объектов мысли: это значит только, что она результат далеко идущего обобщения и потому независима от частных особенностей объектов мысли» [Рубинштейн, 2003, с. 157].

Логика – наука о законах и формах правильного мышления. Под мышлением в философии понимают высшую форму познавательной деятельности, представляющую процесс отражения объективной действительности в сознании человека.

Мышлению предшествует чувственное познание действительности в формах ощущения, восприятия, представления, изучения фактов, наблюдения над явлениями и т.д.

Мышление – это высший продукт особым образом организованной материи – мозга, активный процесс отражения объективного мира в понятиях, суждениях, умозаключениях, индукции и дедукции, анализе и синтезе, в создании гипотез и теорий и т.п. Мышление существует лишь в неразрывной связи с трудовой и речевой деятельностью, свойственной лишь человеческому обществу. Результаты мышления фиксируются в языке в виде мысли.

Способность мышления к обобщенному отражению действительности выражается в способности человека образовывать общие понятия.

Способность мышления к опосредованному отражению действительности выражается в способности человека к акту умозаключения логического вывода, доказательства. Системы понятий образуют научные теории. Образование научных понятий связано с формулированием соответствующих законов.

Мышление характеризуется своими законами и формами.

Формирование логического мышления младшего школьника основано на умениях:

– анализировать и находить в изучаемом материале самое главное, существенное,

– сравнивать и обобщать предметы, явления, процессы так, чтобы понять их суть,

– убедительно доказывать и отстаивать свою точку зрения.

Если логическое мышление – это решение задач, которое с начала и до конца осуществляется на основе понятий, суждений и умозаключениях, то логичное мышление – это эффективное логическое мышление, обязательно предполагающее корректное соблюдение законов и правил логики. В процессе обучения логическое мышление обучающихся становится логичным Мышление изучают многие науки: психология, философия, кибернетика. Но в первую очередь изучением законов правильного мышления занимается математическая логика.

Проблемы развития основ логического мышления решаются при работе над заданиями творческого и поискового характера. В учебниках «Математика» 1-4 классов серия заданий творческого и поискового характера. К примеру, задачи с требованием продолжить (дополнить) ряд чисел, числовых выражений, равенств, значений величин, геометрических фигур – это фактически использование аналогии при их решении. Есть задания, требующие провести классификацию объектов чисел, равенств, значений величин, геометрических фигур по заданному признаку.

Исходя из того, что такие мыслительные операции, как анализ, синтез, сравнение, обобщение, классификация и аналогия являются продуктивной деятельностью младших школьников, связанной с активной работой мышления, необходимо подчеркнуть включение этих операций в процесс усвоения математического содержания, как одной из важнейших условий развивающего обучения, оказывающего позитивное влияние, как на творческую деятельность субъекта, так и на развитие его психических функций.

В ФГОС НОО приведен перечень учебно-логических умений, которыми необходимо овладеть младшему школьнику: анализ и синтез; сравнение; обобщение и классификация; определение понятий; доказательство и опровержение; определение и решение проблем.

Умение выделять признаки предметов, устанавливать между ними сходство и различие – основа приема классификации.

Николай Иванович Кондаков, автор известного логического словаря, определяет классификацию как распределение предметов какого-либо рода на классы согласно существенным признакам, присущим предметам данного рода и отличающим их от других родов [Кондаков, 2013, с. 215].

Алевтина Варфоломеевна Тихоненко подчеркивает то, что предлагая учащимся задания на классификацию, следует учитывать следующие условия:

– ни одно из подмножеств разбиение не пусто;

– подмножества попарно не пересекаются;

–объединение всех подмножеств составляет данное множество [Тихоненко, 2008, с. 255].

Задания, связанные с классификацией, формулируются в следующим образом: «Разбейте на 2 группы по такому-то признаку»; «По какому признаку можно разбить на 2-3 класса (группы)»; «Уберите лишнее»; «Что общего?»; «Чем похожи?» и т. д.

В практике работы начальной школы учителя широко используют задания на классификацию следующих видов:

Подготовительные задания, сформулированные в виде: «Уберите», «Назовите лишний», «Нарисуйте предметы такого же цвета, формы, размера», «Дайте название группе предметов», «Что изменилось? ».

Задания, в которых основание классификации указывает учитель («Разбейте множества геометрических фигур на два класса по свойству «иметь хотя бы один прямой угол», «все углы прямые» и другое).

Задания, при выполнении которых основание классификации указывают учащиеся к примеру, (в один класс попадут все числовые выражения, значения которых равны 10, в другой – все остальные).

Интересные задания на классификацию рассматриваемых объектов представлены в программе «Школа России»: «Какие фигуры изображены на рисунке, на какие две группы их можно разделить? »

Достаточно широко используется в начальной школе прием аналогии. По определению Н.И. Кондакова, «аналогия – это сходство предметов, понятий в каких-либо свойствах, признаках или отношениях, причем таких предметов, которые в целом различны» [Кондаков, 2013, с. 29].

Умозаключение по аналогии представляет собой логический вывод, в результате которого достигается знание о признаках одного предмета на основании знании того, что этот предмет имеет сходство с другими предметами. Так учитель говорит: «Сделай по аналогии», «Решите аналогично», «Рассуждайте аналогично».

Например, учащиеся по аналогии рассматривают умножение двузначного числа на однозначное. По аналогии со сложением двузначных чисел рассматривают сложение трехзначных чисел. Для этой цели предварительно решают примеры на сложение (вычитание) двузначных чисел.

В результате их выполнения выявляется, что в рассматриваемых случаях сложения и вычитания числа записываются одно под другим (единицы под единицами, десятки под десятками, сотни под сотнями) и сложение (вычитание) трехзначных чисел, так же как и сложение (вычитание) двузначных нужно начинать с единиц нижнего разряда.

Таким образом, для правильности умозаключения по аналогии необходимо выделить существенные признаки рассматриваемых объектов. Для формирования умения выполнять умозаключения по аналогии необходимо помнить, что аналогия основана на сравнении, поэтому ее успех зависит от того, насколько учащиеся умеют выделять признаки рассматриваемых объектов, устанавливать их сходство и различие. Н.Б. Истомина отмечает, что для использования приема аналогии необходимо:

– иметь два объекта рассмотрения, один из которых известен, другой сравнивается с ним по каким – либо признакам;

– в доступной форме разъяснить суть приема аналогии, приведя конкретный пример;

– для правильных действий по аналогии необходимо в конкретной ситуации сравнить существенные признаки объектов [Истомина, 2015, с. 178].

Общие закономерности логического и алгоритмического мышления, развившиеся вплоть до навыков и умений в работе над одним содержанием и решением задач одного типа переносятся в мыслительную деятельность с другим учебным содержанием и решением новых учебных задач.

По определению Н.И. Кондакова обобщение – это мысленное выделение существенных свойств, принадлежащих некоторому классу предметов; переход от единичного к общему [Кондаков, 2013, с. 344] .

Прием обобщения, используемый в начальной школе при обучении математике, заключается в выделении существенных признаков математических объектов, их свойств и отношений.

По мнению Алевтины Варфоломеевны Тихоненко и Маргариты Маратовны Русиновой, для получения правильного обобщения необходимо:

– предложить систему математических объектов, задания, вопросы, способствующие целенаправленному наблюдению и сравнению;

– рассмотреть достаточное число частных объектов (примеров, задач, фигур, понятий и т. п.), в которых повторяется та закономерность, которые учащиеся должны подметить;

– варьировать виды частных объектов, то есть использовать предметные ситуации, схемы, таблицы, чертежи, модели, предлагая отыскать в каждом виде объектов одну и ту же закономерность;

– помогать учащимся обогащать свои наблюдения, задавая наводящие вопросы, уточняя и корректируя те формулировки, которые они предлагают [Тихоненко, Русинова, 2008, с. 257].

Н.В. Мельник в своей статье «Развитие логического мышления при изучении математики» пишет, что прежде всего из урока в урок нужно развивать у ребенка способность к анализу и синтезу. Острота аналитического ума позволяет разобраться в сложных вопросах. Способность к синтезу помогает одновременно держать в поле зрения сложные ситуации, находить причины между единичными явлениями, овладевать длинной цепью умозаключений, открывать связи между единичными факторами и общими закономерностями. Критическая направленность ума предостерегает от поспешных обобщений и решений. Важно формировать у ребенка продуктивное мышление, т. е. способность к созданию новых идей, умению устанавливать связи между фактами и группами фактов, сопоставлять новый факт с ранее известным. Продуктивность мышления младших школьников проявляется пока ограниченно. Но если ребенок выдвигает идею не новую для взрослых, но новую для коллектива или для самого себя, пусть известное для других, – это уже показатель продуктивности его мышления [Мельник, 2014, с. 63].

Михаил Николаевич Шардаков определяет анализ как процесс целенаправленного выделения частей предметов или явлений действительности в их признаках и свойствах, а также связей и отношений между ними с целью более полного и глубокого их изучения [Шардаков, 2015, с. 100].

Процессы анализа и синтеза, а также закономерности их развития исследовались С.Л. Рубинштейном, М.Н. Шардаковым в процессе изучения учащимися разных учебных предметов.

Аналитическая деятельность может совершаться у учащихся уже в процессе практических действий с предметами, например при использовании первоклассниками палочек при обучении счету. Аналитическое мышление школьников развивается от элементарного анализа предметов и понятий до более сложных и глубоких.

Кондаков Николай Иванович определил синтез как процесс в результате которого части целого соединяются вместе, составляя их сумму [Кондаков, 2013, с. 406].

Ученые, исследующие процесс анализа и синтеза отмечают, что синтез не является механическим соединением частей в целое, он не просто сумма частей целого. Синтез – это качественно новый результат, некое новое знание действительности.

Анализ и синтез являются как основные формы мыслительной деятельности конструирующими элементами всех других форм мышления. Мышление ни в одной из своих форм, также как и логическое и алгоритмическое мышление, не совершается без анализа и синтеза.

Так, аналитическое изучение предметов и явлений обычно совершается путем сравнения, что позволяет вскрыть существенные и несущественные признаки и свойства, связи и отношения определенной группы предметов или явлений. Выделенные путем анализа существенные признаки и связи абстрагируются, а синтез и обобщение их ведет к получению теоретических, обобщенных знаний. Младший школьник, анализируя при решении задач, одновременно абстрагирует операции с числами от конкретных множеств и синтезируя, приходит к отвлеченному обобщенному знанию соответствующих операций только над числами.

По мнению Николая Ивановича Кондакова, сравнение – это установление сходства и различия между предметами и явлениями действительности [Кондаков, 2013, с. 408].

Сходство рассматривается в сопоставлении с тождеством и различием. При тождестве говорят: «То же самое», «Эквивалентно тому-то». При сходстве рассматриваются некоторые общие закономерности, одинаковые свойства, качества или отношении между сравниваемыми объектами.

В процессе учебной деятельности, чтобы наиболее глубоко развить логическое мышление необходимо также сравнивать в форме противопоставления заключающегося в однородном перемежающемся изучении двух объектов и явлений. Учащиеся при помощи сравнения в виде противопоставления хорошо усваивают двустороннюю связь понятий «больше – меньше на столько-то единиц». Например, пять больше трех на два, а два меньше пяти на три. При использовании сравнения в виде противопоставления, школьники осмысленно усваивали понятие разносторонние отношения [Шардаков, 2015, с. 101] .

В объективной действительности между предметами и явлениями имеются связи, характерные для родового и видового понятий, общего и единичного. То, что свойственно определенному роду, присуще и относящимся к нему видам, а то, что присуще данному общему, свойственно и единичным явлениям, составляющим общее. Бесконечно повторное отображение таких связей выражается в мыслительной деятельности в форме дедукции.

Основная функция дедуктивных умозаключений как особой формой логического мышления состоит в том, что наша мысль идет от общего (понятия, закона, правила) к единичным предметам, явлениям, что мы делаем выводы относительно единичных предметов, объясняя их соответствующими известными правилами или законами.

Прежде всего, при помощи дедуктивной мыслительной работы учащиеся усваивают разнообразные конкретные знания на основе ранее изученных общих правил или законов. Дедуктивные умозаключения, совершаясь посредством анализа, синтеза и сравнения, сами составляют конструирующий элемент конкретизации, определения причинно-следственных, а также других связей и отношений, усвоения понятий, классификации и других форм мышления.

Михаил Николаевич Шардаков пишет, что при изучении единичных предметов или явлений на основе индуктивного мышления заранее предполагается, что учащиеся получат знания о каких – либо новых понятиях, правилах.

Индукция в процессе учения служит не только для собирания отдельных фактов, отдельных случаев. Для получения обобщений в виде понятий, законов.

Индукция и дедукция – две стороны единой индуктивно – дедуктивной мыслительной деятельности. На основе аналитико-синтетического изучения отдельных предметов или явлений путем индукции делается обобщение, и усваиваются общие понятия, законы или правила [Шардаков, 2015, с. 100].

На основе изучения и анализа педагогической и методической литературы понятие «логическое мышление младших школьников» в образовательном процессе рассматривается нами как динамическое направленное по линии математических знаний, приобретаемое им в результате учебного взаимодействия с учителем и регулирующее его учебную деятельность, качество личности, представленное совокупностью компонентов: словесно-логическое, абстрактное (понятийное) мышление.

Михаил Николаевич Шардаков пишет то, что развитие логического и алгоритмического мышления у младшего школьника выражается:

– в качественном развитии и изменении практически действенного, образного и понятийного теоретического мышления.

– в изменении форм соотношения образного, практически – действенного и теоретического мышления в зависимости от содержания мышления, уровня развития и обучения.

– в совершенствовании форм мышления: анализа, синтеза, индукции, дедукции, понятия, классификации, систематизации.

– в формировании навыков мыслительной деятельности.

– в развитии осознания процессов своего мышления и организации целенаправленного его течения.

1.2. Система работы по формированию логического мышления
у младших школьников

А.В. Белошистая и В.В. Левитес под логическим мышлением понимают способность и умение ребенка младшего школьного возраста самостоятельно производить простые логические действия (анализ, синтез, сравнение, обобщение, аналогия, классификация и др.), а также составные логические операции (построение рассуждения с использованием различных логических схем – индуктивной или дедуктивной). Целенаправленная работа Анны Витальевны Белошистой и Веры Владимировны Левитес для формирования логического и алгоритмического мышления у младших школьников привели их к некоторым методическим находкам и позволила выстроить систему заданий для индивидуальной работы с детьми по развитию логического мышления. Разработанные ими в ходе эксперимента материалы предназначены детям 6-7 летнего возраста и ориентированы на начало «с нуля», т. е. на ребенка, не имеющего подготовки. Формирование простых логических действий, также приемов мыслительной деятельности является целью системы заданий, которая основывается на использовании логического конструирования преимущественно на образном математическом материале. Введется систематическая работа по этим материалом и уже к концу первого класса учащийся постепенно готовится к восприятию и пониманию сложных логических структур.

Содержательная основа системы заданий А.В. Белошистовой и В.В. Левитес для первого класса связана с выделением, прослеживанием, распределением и изменением различных признаков и характеристик объектов. Этап построения системы развития логического мышления ребенка полностью выстроен заданиями, которые направлены на активизацию и развития наглядно – образного мышления с помощью: моделями фигур, использованием рамки – трафарета и т.д.

Охарактеризуем систему заданий.

1) задания на выделение признаков у одного или нескольких объектов. Их цель – обратить внимание ученика на значимость того или иного признака объект для выполнения заданий. Предлагаются задания на опознание этого признака, на группировку объектов по выбранному признаку (цвет, размер, форма и т. п.). При этом задание оформлено в виде инструктивного письма графической формы, что позволяет работать даже ребенку, который не умеет читать. Пример: «Раскрась картинку по заданию».

2) задания на прямое распределение признаков. Признаки распределения: цвет, форма, размер. Пример: «Помоги фигуркам найти свой дом».

3) задания на распределение с использованием отрицания одного из признаков.

4) задания, связанные с изменением признака. Графически эти задания оформлены в виде «волшебных ворот», проходя через которое предмет изменяет один из указанных признаков. Пример: «Замени форму вагонов по заданию и нарисуй поезд после прохода через волшебные ворота».

5) те же виды заданий, но трансформированные в другую графическую форму – матрицы (прямоугольные таблицы). Этот графический вид более формализованный, чем предыдущий, но он широко используется в различных областях (математика, информатика и др.). Фактически простейшие матрицы – это то же самое распределение признаков, однако иная графическая форма (лишенная элемента движения, а значит, и жизненной реальности, от которой весьма зависим ребенок этого возраста, мыслящий конкретно) менее понятна ученику 6-7 лет и требует постепенной адаптации. Целесообразно сначала предложить ему задание на матрице с использованием уже знакомого «инструктивного письма».

6) задания на поиск недостающей фигуры, также оформленные в виде неполной матрицы (таблицы). Умение справляться с заданиями такого вида традиционно считается показателем высокого уровня умственного развития. Анализ формы представления такого задания показывает, что от традиционной (полной) матрицы оно отличается отсутствием задающих строк и столбцов. Другими словами, если в традиционной таблице требуется по заданным строкам и столбцам («причина»), используя принцип сочетания признаков, заполнить пустые клетки («следствие»), то в таблице на поиск недостающего элемента заполнение пустой клетки («следствие») требует восстановления опущенных задающих строк и столбцов. Например, задание заполнить пустые клетки, соблюдая определенный принцип.

7) представляет те же виды заданий, но трансформированные в новую графическую форму – алгоритмическую схему. Цель таких заданий – научить ребенка читать и понимать схематическую запись алгоритма. Линейные алгоритмы традиционно используются на уроках математики в начальной школе: на устном счете учитель приводит цепочки вычислений. Оформление такой цепочки приближает ее к классической записи алгоритма. Следует отметить, что классическая форма записи алгоритма достаточно формализована и привыкание к ней ребенка является довольно длительным процессом. Однако сама эта форма вызывает у детей интерес и позволяет достаточно быстро вводить в работу как разветвляющийся алгоритм, так и цикличный.

Все семь видов заданий, заложены в основу систему заданий для развития логического и алгоритмического мышления разработанной Анной Витальевной Белошистой и Верой Владимировной Левитес. Они подчеркивают то, чтобы максимально стимулировать индивидуальные способности младшего школьника и обеспечить его дальнейшее развитие, не дается никаких предварительных инструкций типа «раскрасьте в указанный на веточке цвет». Это лишает ребенка возможности самостоятельно догадаться, выявить признак, закономерность и т.п. Необходимо сначала предложить ученику самому определить смысл задания, не читая его текст. Графического оформления задания достаточно, чтобы при определенном умственном усилии ребенок сам мог сообразить, что нужно сделать. Это позволяет активно влиять на развитие сильного самостоятельного типа мышления, логической интуиции и самоконтроля у ребенка. Текст задания предназначен, скорее, учителю, чтобы в случае необходимости оказать ученику дозированную помощь (т.е. ту минимальную помощь, которая позволит ребенку дальше двигаться самостоятельно) Они подчеркивают: « Если практика показывает, что простые логические действия в определенной мере формируется у каждого человека стихийно, то составные логические операции, имеющие более сложный и комплексный характер, у большинства людей сами по себе не формируются, их развитие требует специальной целенаправленной методической работы». [Белошистая, Левитес,2006, с.35]. Дадим теперь характеристику развития логического мышления младших школьников, представленную в наиболее применяемых в современной начальной школе учебниках математики: Работа по учебнику «Моя математика» (авторы Т.Е. Демидова, С.А. Козлова, А.Л. Тонких и др.) способствует развитию общеучебных умений школьников и позволяет достигать высоких результатов в усвоении знаний, умений и навыков. В формировании темы и целей урока участвуют учащиеся, вырабатывают с учителем алгоритм выполнения заданий.

Светлана Александровна Козлова обращает внимание на то, что в настоящее время много говориться о необходимости нового типа образовательного результата, ориентированного на решение реальных жизненных задач. Под этим понимается личность, которая обладает набором ключевых компетенций или общеучебных умений. Про уровень логической культуры у младших школьников нельзя сказать, что он сформирован на отлично. И в чем же причина? Ведь почти все современные учебники математики содержат специальные задания для развития логического мышления [Козлова, 2006, с. 23]. С.А. Козлова видит проблему в следующем, она в своей статье «Развитие логического и алгоритмического мышления у дошкольников и младших школьников», пишет, что элементы математической логики изучаются в любом начальном курсе математики как неотъемлемая часть обучения предмету и рассредоточены по всему курсу математики начальных классов. Видимо, дело в том, что в большинстве существующих пособий и учебников основное внимание уделяется развитию предметных умений: решать текстовые задачи, уравнения, примеры и т.д. А учебный материал представляет набор заданий, где логическая составляющая не вычленена в явном виде. Считается, что при выполнении подавляющего большинства заданий учащиеся строя цепочку рассуждений, используют не дедуктивный способ, а индуктивный. При оценивании результатов, в первую очередь уделяется внимание степени именно сформированности предметных умений. [Козлова,2006,с.23].

С.А. Козлова, как и А.В. Белошистая и В.В. Левитас, пишет, что большинство современных учебников для начальной школы содержит задания направленные на интеллектуальное развитие ребенка. Однако при этом задания не выстроены в систему, а даются, как правило, со «звездочкой» (только для «сильных» учеников) и специальная методическая работа с ними отсутствует, то результативность работы оказывается не столь высокой, как хотелось бы [Там же. С.23]. Светлана Александровна Козлова подчеркивает то, что при работе с этими задачами последовательно и целенаправленно формируются приемы мыслительной деятельности, развивается логическая интуиция и словесно-логическое мышление (с опорой на осознанное использование словесно-логических моделей с употреблением связок «и», «или», «если .., то …», а также кванторов общности и существования – слов «все», «всякий», «каждый», «любой»). С точки зрения развития словесно-логического мышления схематическое изображение алгоритмов является еще одной интересной моделью для детей. Опираясь на эту модель, они могут довольно эффективно строить цепочки логических рассуждений [Козлова, 2006, с. 23].

В первом классе система заданий начинается с заданий на выделение изученных признаков (цвет, размер, форма, вкус и т.д.) у одного или нескольких объектов. Детям систематическими предлагается разбивать заданную совокупность на группы , объединять объекты в соответствии с найденными признаками, находить закономерность в ряду.

Даются задания на классификацию, представленные в виде таблицы. Это более сложная форма задания для ребенка, которая требует довольно высокого уровня сформированности умения работать с отвлеченными моделями [ Белошистая, 2009, с. 26].

Пример: Катя нарисовала домик-таблицу. Какие фигуры здесь есть? Какие фигуры нарисованы на каждом «этаже»? В каждом «подъезде»? [Демидова, 2005, с.4].

Задания на поиск в таблице недостающей фигуры, для выполнения этого задания требуется высокий уровень сформированности приемов логических действий.

В дальнейшем задания на классификацию неразрывно связаны с развитием у детей, составлять логические цепочки. Во втором классе анализируется истинность и ложность высказываний, а в третьем с кванторами общности и существования.

Анализируя содержание существующих программ, учебников, отмечаем, что проблема формирования логического и алгоритмического мышления наиболее полно решается в программах «Гармония» Н.Б. Истоминой, «Начальная школа 2100…» Л.Г. Петерсон. Серьезное внимание уделяется построению алгоритмической и логической линии, получившие свое развитие в процессе изучения арифметических и алгебраических вопросов.

Постепенно учащиеся овладевают умениями выделять алгоритм своих действий. Например, правило сложения можно сформулировать так: чтобы проверить сложение вычитанием, нужно:

– из суммы вычесть одно из слагаемых;

– сравнить полученный результат с другим слагаемым;

– если полученный, результат равен другому слагаемому, сложение выполнено верно;

– в противном случае надо искать ошибку.

В учебнике Л.Г. Петерсон для 1 класса используется приём классификации. Задания формулируются так: «Догадайся, какой предмет лишний».

Учебно-методическая программа «Начальная школа ХХI века» под редакцией профессора Натальи Федоровны Виноградовой разработана на основе Концепции стандарта второго поколения, требований к результатам освоения основной общеобразовательной программы начального общего образования.

Важной составляющей линией логического развития ребенка является его обучение действиям классификации и аналогии по заданным основаниям и правильность выполнения задания.

Младшие школьники знакомятся с математическими высказываниями, логическими связками, составляющими основу логической формы предложения, используемой в логических выводах.

В 1 классе изображаются результаты сравнения в виде граф с цветными стрелками. Решение арифметических текстовых задач на нахождение большего или меньшего данного числа на несколько единиц.

Во 2 классе составляются числовые выражения и логические операции совершаются над ними.

В 3 классе проводится алгебраическая пропедевтика и работа ведется с буквенными выражениями. На последующих уроках вводятся примеры верных и неверных высказываний. Эта работа будет продолжаться и в 4 классе.

Учебники математики по программе «Школа России» (авторы учебников – М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.В. Степанова, Н.Ф.Вапняр) содержат текстовые задания для развития логического мышления младших школьников уже с первого класса. Данные задания подаются в учебнике как дополнительные (они напечатаны в нижней части страницы под синей чертой курсивным шрифтом).

Например, «соединение элементов в единое целое», «вырежи из Приложения нужные фигуры и составь из них домик, рыбку и т.д.», задания, которые направлены на развитие анализа и синтеза. Задания на поиск различных признаков предмета. Интересные задания на классификацию рассматриваемых объектов: «Какие фигуры изображены на рисунке. На какие группы их можно разделить?» и другие [Моро, Бантова, 20014, с. 14].

Учебник математики для первого класса авторов М И. Моро и др. содержит текстовые задания для развития логического мышления младших школьников. Задания подаются в учебнике как дополнительные (они напечатаны в нижней части страницы под синей чертой курсивным шрифтом), учителя часто обращаются к ним.

Первое такое задание встречается уже на с. 10 части 1 учебника. Тема урока «Последовательность событий во времени».

встретил позже, чем но раньше, чем . Кого из них встретил первым? Вторым?

Рис. 1.1. Последовательность событий во времени

Дети впервые обращаются к таким характеристикам порядка следования событий, как раньше и позже. Практика показывает, что дети с трудом осваивают эти характеристики и поэтому долго путаются в употреблении слов раньше и позже. Поскольку в дошкольной педагогике используются другие слова: сначала и потом.

При определении системы и методических подходов к ознакомлению с письменными приемами выполнения арифметических действий за основу принята оправдавшая себя в практике школы алгоритмизация объяснений. Все они даются в виде четко сформулированной последовательности шагов, которые должны быть выполнены. При рассмотрении каждого частного случая сложения, вычитания, умножения, деления четко выделены основные этапы и план рассуждений, подлежащие усвоению каждым учеником [Петрова, 2000, с. 12].

Задания, которые направлены на развитие анализа и синтеза. Например, «соединение элементов в единое целое», « вырежи из Приложения нужные фигуры и составь из них домик, кораблик, рыбку». Задания на поиск различных признаков предмета. Например, «сколько углов, сторон и вершин у пятиугольника?». Задания на узнавание или составление объекта по заданным признакам, например, «какое число идет при счете перед числом 6? Какое число следует за числом 6?», «составь по краткой записи задачу и реши её».

Задания на рассмотрение данного объекта с точки зрения различных понятий. Например, «составь по рисунку разные задачи и реши их», «постановка разных видов заданий к данному математическому объекту: к концу учебного года у Лиды осталось 2 чистых листа в тетради по русскому языку и 5 чистых листов в тетради по математике. Поставь к этому условию сначала такой вопрос, чтобы задача решалась сложением, а потом такой вопрос, чтобы задача решалась вычитанием». Интересны задания на классификацию рассматриваемых объектов: «Какие фигуры изображены на рисунке, на какие две группы их можно разделить?» [Моро, Бантова, 2003, с. 14].

В учебниках М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой, С.В. Степановой, Н.Ф. Вапнияр, есть логические задания с комплексной направленностью. Например, «Вася выше Саши на 8 см, а Коля на 3см. На сколько сантиметров самый высокий мальчик выше самого маленького?», «магические квадраты: расставьте числа 2; 4; 5; 9; 11; 15 так, чтобы по всем линиям в сумме получилось 24». Задания на сравнение: «сравни уравнения в каждом столбике и скажи, в котором из них неизвестное число больше. Проверь вычислением»

х + 37 = 78 90 – х = 47

\х – 28 = 32 45 + х = 63

х + 37 = 80 90 – х = 50

х – 28 = 22 45 – х = 68 [Моро, Бантова, 2014. с. 29].

Как правило, детей учат решать задачи по действиям, с опорой на которые и составляются математические выражения. Уравнивая величины, дети устанавливают разностное отношение между ними, фиксируемое с помощью выражений «больше на», «меньше на», что позволяет приступить к раннему решению текстовых задач, включающих эти отношения. Схема к задаче появляется «синхронно» с чтением текста: текст читает учитель, структурируя его в соответствии с возможностью изображения заданных величин и отношений между ними. Решение записывается с помощью буквенного выражения, равенства или уравнения [Система Д.Б. Эльконина – В.В. Давыдова, 2001, с. 185].

Также присутствуют задания с «ловушками». Например при изучении задач на введение понятия части и целого, выполняя такие задания с «ловушками», где часть может оказаться больше, чем целое составлено без учета частей, дети устанавливают отношения между данными понятиями. Установление связи между сложением и вычитанием величин на основе понятия части и целого позволяет соотнести целое с суммой и уменьшаемым, а части – со слагаемым или вычитаемым и разностью и увидеть, что разные действия:

А + В = С, С – А = В или С – В = А - характеризуют одно и тоже отношение между величинами. Нахождение неизвестного при решении уравнений опирается не на правила, а на отношение между частями и целым, которое представлено в виде графической модели (схемы).

К концу дочислового периода у учащихся складывается содержательное расчлененное представление о величинах, их свойствах, операциях над ними (сложение, вычитание, сравнение), свойствах этих операций, свойствах равенств и неравенств. Формируются умения решать уравнения и задачи в буквенно – знаковой форме, складываются благоприятные предпосылки для формирования у учащихся понятия области допустимых значений переменных, входящих в математическое выражение, уравнение или задачу.

Во втором классе развитие алгоритмического мышления формируется в рамках задачи измерения величины системой мерок с заданным или выбранным отношением, где сначала определяется количество необходимых для измерения мерок (это значит, становится известным, сколько цифр будет в записи числа), а лишь затем производится сама операция измерения (это значит, что определяется цифра каждого разряда), что позволяет впоследствии задать операционный состав способа выполнения любого арифметического действия как последовательного выполнения двух операций: определение количества цифр (разрядов) в искомом результате выполняемого действия и нахождение цифры, соответствующей каждому из этих разрядов.

В третьем классе при изучении действия умножения и деления предусматривается начать с рассмотрения этих действий в общей (абстрактной) форме с помощью моделей (при умножении в качестве средств моделирования должны быть использованы линейные и плоскостные схемы), а также обеспечен переход от графических к символическим (буквенным) моделям (формулам). Овладение умением строить графические модели умножения и деления, осуществлять переход от этих моделей к буквенными формулам и обратно является одной из важнейших задач этого этапа обучения.

Следующей учебной задачей является задача конструирования способа умножения многозначного числа на многозначное, в основе которого лежит умение умножать многозначное число на однозначное.

Как правило, детей учат решать задачи по действиям, с опорой на которые и составляется математическое выражение. Такой способ обучения решения задач есть не что иное, как обучение от частного к общему, в то время как обучение в рамках системы Д.Б. Эльконина – В.В. Давыдова должно строиться с точностью да наоборот: от общего к частному.

Реализация описанного математического содержания возможна лишь при усвоении готовности учителя организовать сотрудничество детей, требует от него особой организации учебной деятельности школьников в форме постановки и решения ими учебных задач посредством специфических учебных действий [Система Д.Б. Эльконина – В.В. Давыдова, 2001, с. 185].

Единство дидактики, методики и практики представляет собой система Леонида Владимировича Занкова. Среди всех академических предметов, первое место по трудности, отводится математике, как самой абстрактной из наук.

Многие учителя, работающие по системе Л.В. Занкова, убеждены в том, что развитие математических умений, обеспечивается в основном развитием математического стиля мышления.

Дидактическая система Л.В. Занкова направлена на общее развитие школьника. Оценивание ведется по четырехуровневой шкале в соответствии с критериями.

Н.В. Мельник, пишет, что прежде всего из урока в урок нужно развивать у ребенка способность к анализу и синтезу. Острота аналитического ума позволяет разобраться в сложных вопросах. Способность к синтезу помогает одновременно держать в поле зрения сложные ситуации, находить причины между единичными явлениями, овладевать длинной цепью умозаключений, открывать связи между единичными факторами и общими закономерностями. Однако, как это делать, учитель не всегда знает. Нередко это приводит к тому, что развитие логического мышления в значительной мере идет стихийно, поэтому большинство учащихся даже старших классов не овладевают начальными приемами логического мышления, а этим приемам необходимо учить младших школьников [Мельник, 2014, с. 63].

А.В. Белошистая и В.В. Левитес в своей статье «Развитие логического и алгоритмического мышления младшего школьника», пишут, что цель таких заданий – это развитие логических приемов умственных действий (сравнение, обобщение, синтез, анализ, классификация и др.). Однако эти задания часто воспринимаются учителем как дополнительные и необязательные (в связи с тем, что даются на страницах учебников эпизодически и, главным образом, в завершении материала урока – на полях или в нижней части страницы после основного материала) и потому адресуется в лучшем случае наиболее развитым ученикам. При этом опыт показывает, что отсутствие системы в работе над развитием логического мышления оказывает самое пагубное влияние на уровень сформированности мыслительных умений младших школьников [Белошистая, Левитес, 2015, с. 15].

Т.В. Ульяницкая, рассматривает следующие аспекты методики формирования логического мышления младших школьников (по Н.Ф. Талызиной) и возможности начального курса математики для осуществления данной задачи.

Первое, чему необходимо научить школьника, по мнению автора методики, – это умение выделять в предметах свойства. При этом следует специально формировать у детей умение видеть в предмете множество свойств, для чего «полезно показать им прием сопоставления данного предмета с другими предметами, обладающими другими свойствами» [Талызина, 2006, с. 61].

Для организации деятельности учащихся, направленной на выделение признаков того или иного объекта, можно сначала предложить такие задания:

1) учитель демонстрирует детям предмет и просит рассказать о нём.

2) учитель показывает пары предметов или изображений и предлагает установить сходство или различие между ними.

Следующем шагом является формирование понятия об общих и отличительных признаках предметов, а затем формирование у детей умения отличать в предметах существенные с точки зрения определенного понятия и несущественные свойства. Несущественные свойства – это те, отсутствие которых не влияет на существование объекта, а свойство считают существенным, если оно присуще данному объекту и он не может без него существовать. Здесь важно также показать, что любое существенное свойство является общим для данного класса предметов, но далеко не всякое общее их свойство является существенным.

Рассмотренные выше логические приемы называются приемами сравнения предметов и изменения свойств. Прием сравнения предметов дает возможность выделять в них множество свойств, а прием изменения свойств позволяет отличать существенные свойства от несущественных.

Сравнение предполагает умение выполнять следующие действия:

– выделение признаков у объектов;

– установление общих признаков;

– выделение основания для сравнения;

– сопоставление объектов по данному основанию [Талызина, 2006, с. 63].

По мнению Н.Ф. Талызиной, уже в начальной школе можно приступить к работе над определениями. Однако до этого учащиеся должны усвоить отношения между родовыми и видовыми понятиями. При этом следует обратить внимание на то, что видовое понятие обязательно обладает свойствами родового, а родовое является следующей ступенью обобщения.

Определение – это логическая операция, раскрывающая содержание понятия. Способы определения понятий различны. Определения бывают явные и неявные. Явные определения имеют форму равенства, совпадений двух понятий, одно из которых называется определяемым, а другое определяющим.

Л.П. Стойлова подчеркивает, что при изучении математики в начальной школе чаще всего используют так называемые неявные определения. В их структуре нельзя выделить определяемое и определяющие понятия. Среди них различают контекстуальные и остенсивные. В контекстуальных определениях содержание нового понятия вводится через отрывок текста, через контекст, через анализ конкретной ситуации, описывающий смысл вводимого понятия. Остенсивные определения используют для введения терминов путем демонстрации объектов, которые этими терминами обозначаются [Стойлова, 2002, с. 50].

Формирование логического мышления в процессе обучения математике обеспечивается созданием следующей системы работы:

– систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на формирование логического мышления;

– решение трудных задач с «необычным» условием, в которых предоставляется младшим школьникам возможность порассуждать;

– логическое и осознанное исследование явлений реального мира.

Изучив и проанализировав педагогическую и методическую литературу, можно сделать вывод, что формирование логического и алгоритмического мышления у младших школьников в процессе обучения математике – процесс сложный и непрерывный. Он осуществляется под руководством учителя на всех стадиях процесса обучения.

В Федеральном государственном стандарте начального общего образования выделяются следующие компоненты логических универсальных действий:

– анализ объектов с целью выделения предметов;

– синтез – составление целого из частей, в том числе самостоятельное достраивание с выполнением недостающих компонентов;

– выбор оснований критериев для сравнения, классификации объектов;

– подведение под понятие, выведение следствий;

– установление причинно-следственных связей;

– построение логической цепи рассуждений;

– доказательство;

– выдвижение гипотез и их обоснование.

Анализ современных учебников по математике для начальной школы (учебные пособия Н.Б. Истоминой, М.И. Моро, Л.Г. Петерсон и др.) показал, что большинство из них содержат задания и упражнения, направленные на развитие логического и алгоритмического мышления учащихся, но в основном они не носят системного характера, используются в качестве необязательного материала. Проанализировав статьи из журналов и сборников о формировании логического и алгоритмического мышления младших школьников, мы пришли к выводу, что педагоги, методисты и учителя – практики уделяют должное внимание этой проблеме, разрабатывают, изучают методику формирования логического мышления у младших школьников в процессе обучения математики.

ГЛАВА 2. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
ФОРМИРОВАНИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ
У МЛАДШИХ ШКОЛЬНИКОВ

2. 1. Организация и методика исследования

Сущность экспериментального метода состоит в том, что формирование логического мышления у младших школьников на уроках математики обусловлена невозможностью освоения математических знаний без владения приемов логического мышления. Логическая составляющая начального математического образования напрямую связана с развитием мышления учащихся, привитием ему умений строить умозаключения, давать определения понятиям, выполнять логические операции сравнения, доказательства, сопоставления. Экспериментальное исследование проводилось в рамках уроков математики в течение первой четверти.

Цель экспериментального исследования: теоретически обосновать и экспериментально проверить приемы формирования логического мышления младших школьников при обучении математике.

Основной задачей исследования явилась проверка гипотезы при проведении формирующего этапа эксперимента.

Задачи исследования:

– уточнить понятие «логическое мышления младших школьников» на основе изучения и анализа педагогической и методической литературы;

– описать систему работы над формированием логического мышления на уроках математики;

– экспериментально проверить систему работы над формированием логического мышления в процессе обучения.

Изучив теоретические вопросы по формированию логического мышления у младших школьников в процессе обучения математике, приходим к выводу, что овладение логическим и алгоритмическим мышлением предоставляет неограниченные возможности для общего и в частности математического развития учащихся.

Экспериментальная исследование проводилось в третьих классах на базе казённого государственного учреждения «Общеобразовательная средняя школа №10 г. Актау Республики Казахстан» в течение первой четверти 2015/2016 учебного года. Всего было задействовано 48 учащихся. Экспериментальный класс 3 «Г» (учитель Л.В. Мангитбаева), и поскольку в данном классе проводятся факультативные занятия по развитию логических способностей, он был взят в качестве экспериментального, а контрольный стал 3 «Ж» класс (учитель Арзу Шаваловна Азизова). Данная школа является школой смешанного типа, обучение проводится на двух языках (русском и казахском). С 20016/2017 учебного года школа перешла на 12-летнее образование. В школе обучается 470 учеников, в двух параллелях. Школа работает в режиме 6-дневной рабочей недели, для учащихся 2-11 классов и 5-дневной рабочей недели для учащихся первых классов. Продолжительность уроков во всех классах начальной школы 45 минут.

Основными методами и методиками исследования являются различные методы представления текста задачи их решений направленных на формирование логического мышления младших школьников. Была составлена система развивающих заданий. Все логические задачи разбиты по группам, каждая из них имеет название и рассчитана на определенный возраст. Систематическая работа с логическими заданиями открывает новые возможности в плане развития обобщенных приемов мышления, логики, познавательной активности ребенка.

Для доказательства выдвинутой гипотезы был разработан эксперимент, заключающий в себе 3 этапа (констатирующий, формирующий и контрольный), имеющий целью разработать и апробировать систему заданий для формирования логического и алгоритмического мышления у младших школьников в 3 классе. В эксперименте участвовали две группы учащихся – это экспериментальная и контрольная группа.

Опишем каждый из перечисленных этапов.

На констатирующем этапе эксперимента приняли участие ученики 3 «Г» и 3 «Ж» классов.

Цель: выявить существующий уровень сформированности логического мышления у учащихся 3 «Г» и 3 «Ж» классов казённого государственного учреждения «Общеобразовательная средняя школа №10 г. Актау Республики Казахстан».

Для этого использовались наблюдения за работой детей на уроках математики, ответы на вопросы, выполнение заданий, анкетирование и др.

Учащимся были предложены следующие задания для определения уровня сформированности логического мышления.

Для выполнения заданий учащиеся должны обладать следующими умениями: выделять признаки предметов; узнавать предметы по заданным признакам; сравнение двух или более предметов; умение делить объекты на классы по заданному основанию; выявление существенных и несущественных признаков; соединять элементы в единое целое и включать их в новые связи.

Ниже приведены условия задач, предложенных ученикам на констатирующем этапе (всего 5 заданий).

Задание №1. Выделение признаков предмета.

Цель – выявить уровень умения находить существенные и несущественные признаки предметов у учащихся экспериментального и контрольного классов.

а) С какой цифры начинаются числа:14,18,25? (С цифры 1, 1, 2).

Задание №2. Узнавание предметов по заданным признакам.

Цель – выявить уровень умения узнавать предметы по заданным параметрам у учащихся экспериментального и контрольного классов.

а) Какой предмет обладает одновременно следующими признаками: имеет 3 стороны и 3 угла? (треугольник).

б) Внимательно рассмотрите числа в каждом столбце. Догадайтесь, как они подобраны. Какое число должно стоять вместо знака «?».

42 75 54 21

37 25 45 63

79 100 99 ?

Вместо знака «?» должно стоять число 84 т. к. в каждом столбце первые два числа – это слагаемые, а третье число это их сумма.

в) Вставьте пропущенные числа:

5, 15, … 35, 45; ( 5, 15, 25,35, 45).

В этом заданий нужно установить закономерность ряда чисел.

Задание №3. Сравнение двух и более предметов.

Цель – установить уровень умения учащихся ЭК и КК сравнивать предметы и понятия.

Сравни примеры, найди общее и сформулируй новое правило:

а) 20+21 21+22 22+23 23+24 24+25 25+26.

Вывод: сумма двух последовательных чисел есть число нечетное. Это задание на определение четности и нечетности числа.

Задание №4. Упражнения, направленные на формирование умения делить объекты на классы по заданному основанию.

а) Раздели на 2 группы следующие числа:2,13,3,43,6,55,18,7,9,31:

– однозначные числа: (2, 3, 6, 7,9);

– двузначные числа: (13, 43, 55, 18, 31).

Это задание, позволяющее закрепить позиционность натурального числа.

На формирование логического и алгоритмического мышления у младших школьников большое значение имеют и геометрические задания.

Задание №5. Геометрическое задание. Задачи на составление заданной фигуры из определенного количества палочек.

а) Дана фигура из 6 квадратов. Надо убрать 2 палочки так, чтобы осталось 4 квадрата.

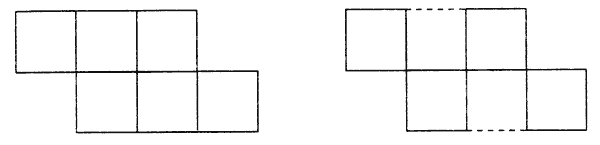
В ходе исследования, подсчитав результаты констатирующего среза, мы получили возможность сделать каждому классу некоторые выводы об уровне сформированности логического мышления у учащихся экспериментального и контрольного классов.

В экспериментальном и контрольном классах логическое мышление у детей сформировано неодинаково. Они допускают ошибки при выделении признаков предмета, сравнивании двух и более предметов, при делении объектов на классы.

Констатирующий эксперимент проводился с целью диагностики существующего уровня сформированности логического мышления на уроках математики у учащихся 3 класса казённого государственного учреждения «Общеобразовательная средняя школа №10 г. Актау Республики Казахстан». Для этого использовалось наблюдение за работой детей на уроках математики и ответы на вопросы.

Формирующий эксперимент, проводился в течение второй и третьей четверти (2015/2016 учебный год).

Представленная работа посвящена изучению одного из структурных элементов учебной деятельности – формированию логического мышления у младших школьников в процессе обучения математике. Использование специальных заданий, приведенных в методической литературе, способствует формированию и развитию логического и алгоритмического мышления.

Цель формирующего эксперимента – разработать и апробировать систему упражнений для формирования логического и алгоритмического мышления в процессе обучения математике в 3 классе в течение второй и третьей четверти.

В связи с этим в формирующем эксперименте использовались упражнения и задания, которые помогали учащимся расширить свои умения и способствовали формированию логического и алгоритмического мышления

Вследствие этого были разработаны и использованы разнообразные системы упражнений и заданий на уроках математики в экспериментальном классе. Эти упражнения были применены в виде логических пятиминуток и дополнительных заданий на этапе актуализации знаний, на этапе закрепления пройденного материала, во время внеклассных мероприятий.

Были разработаны конспекты уроков, подобраны задания и задачи для формирования логического мышления (см. Приложения №№1, 2).

При составлении вариантов заданий по формированию логического и алгоритмического мышления использовались задания и упражнения В.В. Левитес, А.В. Белошистой, Л.Ф. Тихомировой.

Сюжетные задачи, которые приведены, использовались в основном, в виде дополнительного задания. Материал взят из сборника И.Г. Сухина «800 новых логических и математических головоломок». Приведем некоторые из них.

1. Какую отметку впервые в жизни получил по русскому языку Дима, если известно, что он является числом не простым, а составным? ( Дима получил отметку 4, в этой задаче повторяются простые и составные числа).

2. Раздели самое маленькое четырёхзначное число на наименьшее простое и узнаешь, сколько лет не умывался и не чистил зубы великан? (Самое маленькое четырехзначное число – 1000, наименьшее простое число 2, 1000 : 2 = 500. Великан не чистил зубы 500 лет. В этой задаче младшие школьники повторяют позиционность числа, также простые и составные числа).

Следующие задания способствуют формированию логического приёма – сравнение.

1. Прочитайте числа каждой пары. Чем похожи они и чем отличаются? (Задание позволяющее закрепить позиционность натурального числа).

а) 5 и 50 б)17 и 170.

2. Даны числа: 12,16,20,24,28,32.

Чем похожи эти числа и чем они отличаются? (задание, позволяющее определить четность и нечетность чисел и позиционность натурального числа).

Задания на формирование логического и алгоритмического мышления у младших школьников можно составить, используя геометрический материал.

3. Чем отличается четырехугольник от пятиугольника?

Одинаковость (похожесть) четырехугольника и пятиугольника в наличии углов. Различие в количестве углов.

Опишем использованные методики исследования для формирования логического мышления младших школьников.

Первая методика – это систематическое использование на уроках математики и внеурочных занятий специальных задач – заданий, направленных на формирование логического мышления младших школьников:

Рассмотрим методику использования занимательных задач.

Фокусник вынимает шары из шляпы. Мы знаем, что в этой шляпе первоначально было: 3 серых, 1 белый и 2 цветных шара. Сколько среди нижеследующих высказываний вы можете считать наверняка ложных высказываний, если некоторые из них истинные наверняка, а другие высказывания могут быть истинные, а могут быть и ложные, и есть утверждения, наверняка ложные:

а) если он вынет 4 шара, среди них обязательно будет один серый шар;

б) если он вынет 3 шара, будет по крайней мере по одному шару каждого вида;

в) если он вынет 4 шара, будет по крайней мере два шара одного и того же цвета;

г) если он вынет 6 шаров, будет по крайней мере два шара каждого цвета;

д) если он вынет 5 шаров, будет серых шаров больше, чем цветных.

Ответ: а) всегда истинное, так как не серых шаров – 3;

б) может быть истинным (он может вынуть по одному каждого цвета или ложным (так как он может вынуть все три серых шара, или 1 белый и 2 цветных, или по одному каждого цвета);

в) всегда истинно, потому что шары только трех цветов;

г) всегда ложно, так как в шляпе нет 2 белых шаров;

д) всегда ложно, цветных шаров может быть меньше(3 серых и 2 цветных) или столько же (2 серых, 2 цветных и 1 белый ) сколько серых;

е) иногда ложно (2 серых, 2 цветных и 1 белый), иногда исинно ( он может вынуть 3 серых и 2 цветных ).

Следующие задачи – это задачи-смекалки и задачи-шутки.

Какой вес? У продавца были гири: 1 кг, 2 кг и 4 кг, и чашечные весы.

Какой вес он может взвесить с помощью этих гирь, если гири он кладет только на одну чашку весов?

Ответ: Самый маленький вес, который может взвесить продавец с помощью указанных гирь – 1 кг, самый большой:

1 + 2 + 4 = 7 кг .

Можно также взвесить: 2 кг, 4 кг .

Также можно взвесить: 1 + 2 = 3 кг;

1 + 4 = 5 кг;

2 + 4 = 6 кг;

Ответ: можно взвесить любой вес от 1 кг до 7 кг включительно.

Вторая из методик, направленная на формирование логического мышления младших школьников: – это решение «трудных задач» с «необычным» условием, в которых предоставляется возможность порассуждать;

Рассмотрим методику решения занимательных и арифметических задач.

Принцесса хочет блинчики на завтрак, поэтому она сказала своему повару, что она собирается встать и начать кушать в 8 часов утра, и что она хотела бы иметь на завтрак 20 блинчиков.

Повар выпекает блинчик за одну минуту, а Принцесса съедает блинчик за 30 секунд. Во сколько должен встать повар, если он сразу же начинает выпекать блинчики?

А) 7 ч. 40 мин; Б) 7 ч. 40,5 мин; В) 7 ч.49 мин; С) 7 ч. 49,5 мин; Д) 7 ч. 50 мин;

Ответ: (Д)

Принцесса съест все 20 блинчиков за 10 мин, а повар их выпечет за 20 минут, складывается впечатление, что он должен встать на 10 мин раньше Принцессы, т.е. в 7 часов и 50 мин, однако это не так, ведь Принцесса должна начать кушать последний 20 блинчик в 8 часов 9,5 минут, а повар должен испечь его именно к этому времени. Поэтому он должен встать на полминуты раньше, т.е. в 7 часов 49,5мин.

Следующая методика – это обучение решению задач, содержащих математические ребусы и вопросы:

Расшифруй ребус: 8 х * = 8.

Ответ: в этом ребусе число 8 является произведением двух сомножителей:

– первый сомножитель равен 8;

– второй сомножитель неизвестен.

Мы видим, что первый сомножитель и произведение совпадают между собой. Значит, второй сомножитель равен единице.

Ответ: 8 х 1 = 8.

Третья методика, применяемая в эксперименте, – это логическое и осознанное исследование явлений реального мира.

Задача, предложенная учащимся на уроке самлпознания.

На острове живут два типа людей: честные и лжецы. Честные, всегда говорят правду. Лжецы всегда лгут. Однажды мы спросили каждого из 5-ти человек, живущих на этом острове, которые хорошо знали друг друга: «Сколько среди вас честных людей?»

Мы получили следующие ответы: 0, 1, 2, 3, 4.

Сколько же честных людей в этой группе из 5-ти человек?

(а) 0 чел.; (б) 1чел.; (в) 2чел.; (д) 3чел.; (е) 4 чел.; (г) 5чел.;

Ответ: Человек, назвавший число честных – 0 – лжец, так как честный обязательно назовет число, равное или больше единицы.

Так что верить этому человеку, что честных тут нет, нельзя. В группе должен быть обязательно по крайней мере один честный человек.

Все приведенные задачи и задания составлены автором данной выпускной квалификационной работой и утверждены на заседании Совета ГУ «АГКЦО», рекомендованы экспертной комиссией ГУ «АГКЦО» для использования, как для самостоятельного чтения учениками 1-4 классов, так и учителями во внеклассной работе.

Диагностика уровня логического мышления проводилась методами психологического исследования. Для этого были предложены задания, направленные на определение степени овладения логическими операциями:

– выявление способности выделять существенное;

– степень овладения операцией сравнения;

– степень овладения операцией обобщения;

– степень умения классифицировать.

Учащимся были предложены следующие задания:

1. Выделение существенного.

Цель задания: выявить уровень умения у учащихся находить существенные признаки предметов.

Из трёх предложенных рядов слов, в каждом из которых пять слов дается в скобках, а одно перед ними, учащиеся должны за 20 секунд выделить два слова (словосочетания), наиболее существенные для слова, стоящего перед скобками.

Треугольник (четыре угла, острый угол, диагональ, все стороны равны).

Куб (четыре угла, шесть граней, плоская фигура, пространственный).

Окружность (радиус, диагональ, диаметр, форма глобуса).

2. Сравнение понятий.

Цель задания: установить уровень умения учащихся сравнивать предметы, понятия.

Учащимся предъявляют два предмета или понятия. Каждый ученик должен написать на листе бумаги справа – черты различия, слева – черты сходства. На выполнение задания, состоящего из одной пары слов, дается 2 минуты.

1. Шар – круг.

2. Конус – пирамида.

3. Параллелограмм – прямоугольник.

4. Обобщение понятий.

Цель задания: выявить уровень сформированности приёма обобщения у учащихся.

В каждой паре слов учащийся должен определить, что между ними общего. На каждую пару времени отводится 2 минуты.

Квадрат, прямоугольник. (Прямые углы)

Ромб, параллелограмм. (Два острых угла)

5. Классификация понятий.

Цель задания: Выявить уровень сформированности приёма классификации у учащихся.

Учащимся предлагается 5 групп слов. Каждая группа состоит из 5 слов, четыре из которых объединены общим признаком. Пятое слово к ним не подходит. Надо найти и подчеркнуть это слово. На работу отводится 3 минуты.

1. Конус, куб, параллелепипед, ромб, призма. (Ромб)

2. Треугольник, отрезок, длина, квадрат, круг. (Длина).

С учетом предметных связей предлагались следующие задания:

1. Найти неизвестное число:

Селедка Лед

Солистка Лист

72 350 ?

Ответ: число 3. К такому ответу приводят следующие рассуждения. В словах первого столбика исключены две первые буквы и две последние буквы. Значит и в числе надо исключить две первые и две последние цифры.

2. Найти неизвестное число:

Дерево + земля = 11

Турист * спорт = ?

Младшие школьники при решении этой задачи приводят следующие рассуждения.

В слове дерево – 6 букв, а в слове земля – 5 букв, сложив эти числа получим 11. В слове турист – 6 букв, а в слове спорт – 5. Умножив эти числа получим 30.

Большую роль в формировании логического мышления играет задача, которую учащиеся должны решить, опираясь на свои приобретенные знания.

3. Реши следующую задачу. Чтобы распилить доску на несколько частей, ученик сделал на ней шесть отметок. На сколько частей ученик поделил доску?

Уроки, проведённые в рамках формирующего эксперимента, приведены в Приложениях, к примеру, в Приложении №2.

Приведём в качестве примера урок, на котором формируются логические умения.

Тема урока: Составление и решение задач в одно и два действия.

Цель урока: познакомить учащихся с решением задач в два действия и составлением выражения и их письменным объяснением; формировать общую способность искать и находить новые решения, необычные способы; развивать речь, мышление в ходе усвоения таких приемов мыслительной деятельности, как умение анализировать, сравнивать, синтезировать, обобщать выделять главное, доказывать и опровергать.

Следующие задания, были использованы на уроке.

Расставьте в порядке возрастания числа и узнаете его имя:

На слайде даны числа: 23; 30; 45; 52; 60; 74; 91.

Это 23.

В А С И Л И Й

Назовите число 5-го десятка, 8-го десятка, назовите его соседей.

Индивидуальная работа по карточкам.

Кот Василий предлагает поработать по карточкам и распутать клубок.

Соедини с правильным ответом.

80 + 5= 30 59 + 1 = 96

90 + 6 = 39 40 – 1 = 85

47 – 40 = 60 38 – 8 = 7

Выполнение логических заданий:

Игра «Наоборот».

Сумма – разность, день – ночь, час – минута, метр – см, однозначное – двузначное, простая – составная.

Этими терминами мы будем пользоваться на уроке.

«Незаконченное предложение».

Закончить предложения. Слайд №4.

От перестановки слагаемых….

Результат при сложении…

Что имеет условие, вопрос, решение, ответ….

Устный счет.

а) игра « Истина – ложь»

Проверим навыки устного счета. Если с высказыванием согласны подымите карточку зеленого цвета, если нет красного.

– сумма чисел 50 и 9 равна 49

– разность чисел 27 и 7 равна 20

60 увеличить на 7 будет 47

От 45 отнять 5 будет 40

б) Прочитать разными способами примеры и вычислить их. Слайд №5.

68 - 8= 60 37 + 1=38

Соотнесите ответы с темой «Коты».

60 м – расстояние, на которое могут видеть кошки.

38 градусов – температура тела кошки.

Что изменилось? (сравните следующие признаки: цвет, форма, размер).

(Изменение между первой фигурой и второй это форма и размер, между второй и третьей цвет и размер, между третьей и четвертой форма и размер, между четвертой и пятой цвет и размер, между пятой и шестой цвет и форма.

Надо подвести итог урока.

Итоговой контрольной проверочной работой по выявлению сформированности логического мышления третьеклассников является контрольный эксперимент.

Опишем урок, проведённый на контрольном этапе эксперимента.

Форма проведения урока – КВН.

Цель: Проверить уровень приобретенных умений учащихся, эффективность разработанных упражнений и заданий для формирования логического и алгоритмического мышления.

Задачи:

1. Способствовать формированию интереса к урокам математики.

2. Закреплять знания математических терминов, умения выполнять вычислительные действия на изученные случаи умножения, деления, вычитания и сложения.

3. Способствовать развитию логического мышления, речи, памяти, внимания.

Оборудование: компьютер, мультимедиа проектор, презентация.

Вступительное слово.

Учитель. Издавна люди называют математику царицей наук, потому что математика применяется в различных областях знаний. Один из важнейших разделов математики – арифметика.

Арифметика – это наука о числах, свойствах чисел и действиями над ними.

Представление команд:

Учитель. Сегодня в нашем КВН участвуют три команды.

Команды, поприветствуйте, пожалуйста, друг друга.

Поприветствуйте, пожалуйста, уважаемое жюри.

Команды по очереди дружно говорят своё название и девиз.

1 Команда 3 «Г» класс:

Наша команда – «Дважды два».

Девиз: Чтоб врачом, моряком

Или летчиком стать,

Надо твердо на «5» математику знать!

Приветствие:

Наше пожелание всем:

Победившим не хвалиться,

Проигравшим не реветь.

2 Команда 3 «Ж» класс:

Наша команда – «ПУПС»

Девиз: Пусть ум победит силу!

Приветствие:

Желаем нынче воспитать

Такую точность мысли,

Чтоб в нашей жизни все познать,

Измерить и исчислить.

3 Команда 3 «В» класс:

Наша команда – «Квадрат»

Девиз: У нашего «Квадрата»

Все стороны равны.

И наши все ребята

Дружбою сильны.

Приветствие:

Наша команда «Квадрат»

Приветствует собравшихся ребят.

Желаем всем победить,

А себе – не проиграть.

Учитель. Наши команды уже прибыли. Это лучшие математики, которые не унывают, быстро считают, хорошо решают задачи, любознательны, живут всегда весело и дружно. Познакомьтесь с судейской коллегией. Начинаем разминку:

1. Конкурс «Разминка». Слайды 1, 2, 3.

Учитель. Я задаю командам по одной задаче. Если команда не решит свою задачу, за неё эту задачу решает другая команда-та, в которой раньше поднимут руку.

1. Две сардельки варятся 6 минут. Сколько времени будут вариться восемь таких сарделек? Ответ: 6 минут.

2. Шла девочка в Москву и повстречала трех мальчиков. Каждый из них нес по мешку, в каждом мешке по коту. Сколько существ направлялось в Москву? Ответ: 1 девочка.

3. Пять лампочек тускло горели в люстре.

Хлопнули двери, и две перегорели.

Сделать нужно вам малость –

Сказать, сколько ламп осталось? Ответ: 5 лампочек.

2. Конкурс: «Ребусы». Слайд 4.

Учитель. Расшифруйте спрятанные слова. А сможете это сделать только если разгадаете ребусы. Команды отгадывают ребусы. За каждый ребус команда получает балл.

1 команда

АК 3 СА

ПРЕ 100 Л

2

ПА 3 ОТ

100 ЛИЦА

команда

3

100 ЛБ

команда

КИС .

3. Конкурс: «Реши задачку». Слайд 5, 6, 7.

1) 10 солдат строились в ряд,

10 солдат шли на парад.

9/10 было усатых.

Сколько там было безусых солдат? (Один)

2) 10 солдат строились в ряд,

10 солдат шли на парад.

8/10 было носатых.

Сколько там было курносых солдат? (Два)

3) Если Грушам дать по груше,

То одна в избытке груша.

Если дать по паре груш,

То не хватит пары груш.

Сколько Груш? И сколько груш? (3 Груши, 4 груши)

4. Конкурс: «Отгадай слово». Слайды 7, 8, 9.

1) Первое — предлог, второе — летний дом, а целое порой решается с трудом. (Задача)

2) Запись числа 100 состоит из трех букв и трех цифр. Найдите еще число, в записи которого коли­чество букв равно количеству цифр. (1 000 000 – миллион)

3) Возьми число из первого десятка,

Местоимение к нему добавь.

Получишь слово, вот и вам отгадка –

И сможешь маму, папу и себя назвать. ( Семья).

5. Конкурс: «Угадай знак».

Вставьте пропущенные знаки действий «+» или «-».

5 ? 4 ? 3 ? 2? 1= 3 (5 + 4 - 3 - 2 - 1 = 3)

5 ? 4 ? 3 ? 2? 1= 5 (5 + 4 - 3 - 2 +1 = 5)

5 ? 4 ? 3 ? 2? 1= 7 (5 + 4 - 3 + 2 - 1 = 7)

6. Конкурс: «Конкурс капитанов».

Начерти по разному прямоугольники площадью 4 см.

Ответ: прямоугольники со сторонами 4см и 1см; квадрат тоже прямоугольник 2 см и 2 см.

7. Конкурс: «Геометрический».

Учитель. Мячи сложили пирамидой. Сколько здесь мячей?

Учитель. Команды назовите свои ответы.

8. Конкурс: «Числа в пословицах и поговорках».

1 команда: ... в поле не воин.

Один в поле не воин.

2 команда: … одного не ждут.

Семеро одного не ждут.

3 команда: У … нянек дитя без глазу.

У семи нянек дитя без глазу.

9. Конкурс. «Математические загадки».

Двенадцать братьев

Друг за другом ходят,

Друг друга не обходят.

(Месяцы.)

На лесенке-стремянке

Развешаны баранки.

Щелк да щелк – пять да пять –

Так мы учимся считать. (Счеты.)

Черненькая, хвостатенькая,

Не лает, не кусает,

А из класса в класс

Не пускает. (Двойка.)

4. Награждение победителей.

Учитель. Подсчитаем, сколько баллов получила каждая команда.

Поздравление всех участников и награждение победителей. Победила команда 3 «В» класса.

Заканчивается КВН, спасибо всем за участие. Слайд 10.

Слайд 1

Слайд 2.

Слайд 3

Слайд 4

Слайд 5.

Слайд 6.

Слайд 7.

Слайд 8.

Слайд 9.

Слайд 10.

С целью подтверждения правильности выдвинутой гипотезы, был проведен еще один эксперимент. Ученикам было предложено выполнить систему заданий (6 заданий).

Представим эти задания.

Задание №1.Выделение признака, младшие школьники должны определить лишнее выражение, путем вычисления. Лишнее выражение – Г, так как результат вычисления равен 40, а в остальных случаях – 56.

а) Найди «лишнее» выражение.

А) (8 + 6) ∙ 4

Б) 4 ∙ (8 + 6)

В) (8 + 6) + (8 + 6) + (8 +6) + (8 + 6)

Г) 4 ∙ 8 + 8

Д) 8 ∙ 4 + 6 ∙ 4

Задание №2.Определение предметов по заданным признакам.

Вставьте пропущенные числа (задание на нахождение закономерности).

а) 12,22,…,42,52,…72; (32, 62).

б) 6,12,18,…30,36,…;(24, 42)

Разгадай правила, по которым составлены выражения. Запиши в столбик ещё три выражения по этому же правилу. Найди значения всех выражений.

а) 97 – 70

б) 86 – 60

(Выражения составлены по следующему правилу – каждое последующее выражение будет состоять из двузначного и круглого числа, так чтобы из разность была равна 20.)

Задание №3.Сравнение двух или более предметов.

а) Чем похожи числа 24 и 41? (Задание позволяющее закрепить позиционность натурального числа и четность и нечетность числа).

б) Чем отличается треугольник от четырехугольника? (Задание позволяющие закрепить существенные признаки геометрических фигур).

Задание №4.Упражнения, направленные на формирование умения делить объекты на классы по заданному основанию.

а) Раздели на следующие группы числа:1, 52, 10, 3, 53, 6, 5, 1, 77, 49.

Однозначные числа (1, 3, 1)

Двузначные числа (52, 10, 53, 77, 49)

Четные (52,6,10)

Нечетные (1, 3, 5, 77, 49).

Большой наблюдательности требуют от учащихся логические цепочки, которые нужно продолжить вправо и влево, если такое возможно. Чтобы выполнить задание, необходимо установить закономерность в записи чисел:

1. Восстанови ряд.

а) 6 12 18………. (6, 12, 18, 24, 30, 36..)

б)…..6 12 24…… (3, 6, 12, 24, 48, 96…)

Задание №5. Сравнение предметов и понятий.

а) Сравни примеры, найди общее и сформулируй новое правило:

25+10-10 86+5-5 256+28-28 ( Если к любому числу прибавить и затем вычесть одно и то же число, то получиться первоначальное).

Задание №6.

Реши логическую задачу. Логическая задача предполагает решение без выполнения арифметических действий.

1. На веревке завязали пять узлов. На сколько частей эти узлы разделили веревку? (на 6 частей).

Представленные задания, игры, упражнения вызывают у детей большой интерес. А ведь именно он должен лежать в основе обучения младшего школьника. Интерес поддерживает высокий уровень познавательной активности, что в свою очередь способствует развитию интеллектуальных способностей у младшего школьника. На контрольном этапе учащимся, был проведен КВН, где соревновались две команды :экспериментального и контрольного класса.

В таблицах 2.1, 2.2, 2.3 и 2.4 приведены результаты экспериментального и контрольного класса, констатирующего и контрольного этапов проводимого эксперимента.

Выявленные уровни сформированности логического мышления младших школьников и разработанный инструментарий диагностики (критерии) позволяют отслеживать динамику уровней и результативности формирования логического мышления у младших школьников.

2.2. Результаты экспериментального исследования

В ходе исследования, подсчитав результаты констатирующих срезов, мы получили возможность сделать по каждому классу некоторые выводы об уровне сформированности логического мышления у учащихся экспериментального и контрольного класса. В экспериментальном и контрольном классах, логическое мышление у детей сформировано неодинаково. Они допускают ошибки при выделении признаков предмета, сравнении двух и более предметов, при делении объектов на классы по заданному основанию, при решении логической задачи (все результаты приведены в таблицах). Итоговой контрольной проверочной работой по выявлению сформированности логического мышления является контрольный эксперимент.

Таблица 2.1.

Констатирующий срез определения коэффициента усвоения
логического мышления у учащихся экспериментального класса

№ П/П	Список учащихся	Задания						Коэффициент Усвоения
		1	2	3	4	5	6
1	Айназ	+	+	-	+	+	-	0, 6
2	Нурзиля	+	+	+	+	+	+	1
3	Айдар	+	-	-	-	-	+	0,3
4	Диана	+	+	+	+	+	+	1
5	Данил	+	-	-	+	-	-	0,1
6	Алина	+	+	-	+	+	+	0,7
7	Ильнур	+	+	-	-	+	+	0,6
8	Артур	+	-	-	+	-	-	0,3
9	Камилла	+	+	-	-	+	+	0,6
10	Айназ	-	+	+	-	+	+	0,6
11	Диана	+	-	+	+	+	-	0,6
12	Алия	+	+	-	+	-	+	0,6
13	Айнур	+	+	+	+	+	+	1
14	Реналь	+	+	-	+	+	+	0,8
15	Евгения	+	-	+	-	-	+	0,5
16	Лиана	­-	-	+	-	+	-	0,3
17	Артур	+	-	+	+	-	-	0,5
18	Ильназ	+	+	+	+	+	+	1
19	Эвелина	+	-	+	+	+	+	0,8
20	Алсу	+	+	-	+	+	+	0,8
21	Денис	+	-	+	+	-	+	0,6
22	Индира	+	-	-	-	+	-	0,3
23	Тимур	+	+	+	+	+	+	1
24	Ира	+	+	+	+	+	+	1
Средний коэффициент усвоения		0, 64

Таблица 2.2

Констатирующий срез определения коэффициента усвоения

логического мышления у учащихся контрольного класса

№П / П	Список учащихся	Задания						Коэффициент Усвоения
		1	2	3	4	5	6
1	Дмитрий	+	-	-	+	-	-	0,3
2	Иван	+	+	+	+	+	+	1
3	Аделя	+	+	+	+	-	-	0,6
4	Ольга	+	-	+	+	+	+	0,8
5	Милана	+	-	+	+	-	-	0,5
6	Эвелина	­+	-	-	-	+	-	0,3
7	Сабина	­-	-	+	-	+	-	0,3
8	Рубен	­+	+	+	+	+	-	0,6
9	Карина	+	+	+	+	+	+	1
10	Арина	+	-	+	+	+	+	0,8
11	Валерия	+	-	+	+	-	-	0,5
12	Савелий	+	+	+	+	+	+	1
13	Екатерина	+	+	-	+	-	+	0,6
14	Екатерина	+	-	+	+	+	+	0,6
15	Богдан	+	+	+	+	+	+	1
16	Саша	+	-	+	+	-	-	0,5
17	Александр	+	+	_	+	+	+	0,8
18	Искандар	­-	+	-	-	+	-	0,3
19	Валерия	+	-	+	+	-	+	0,6
20	Карина	+	+	-	+	-	-	0,6
21	Алина	­+	-	-	-	+	-	0,3
23	Денис	+	-	+	+	-	-	0,5
24	Рубен	+	-	-	-	+	-	0,3
Средний коэффициент усвоения		0,63

В таблицах 2.1 и 2.2 приняты следующие обозначения «+» означает, что младший школьник выполнил соответствующее задание без ошибок, знак «–» означает, что младший школьник не выполнил соответствующее задание или выполнил с существенными ошибками.

Коэффициент усвоения определялся как частное от деления числа выполненных заданий к общему количеству предложенных заданий.

Констатирующий этап эксперимента показал, что оба третьих класса находятся на одинаковом уровне формирования логического мышления: количество учеников, выполнивших все задания в каждом классе, по 4 человека. Примерно одинаковое количество учеников справилось лишь половиной заданий.

Результаты контрольного среза показали, что уровень сформированности логического мышления у учащихся экспериментального класса (далее – ЭК), повысился на 0,16%, а у контрольного класса (далее – КК) на 0,08%. В ходе исследования мы наблюдали за 48 младшими школьниками. Проанализировав выполненные задания, мы получили возможность сделать некоторые выводы об уровне сформированности логического и алгоритмического мышления в 3 «Г» классе, использовавшие на своих уроках и внеклассных мероприятиях задания направленные на формирование логического мышления. Доказательством результативности опытно-экспериментальной работы по целенаправленному формированию логического мышления у младших школьников явились данные контрольного эксперимента. Контрольный эксперимент заключался в проведении системы уроков, отражённых в календарно-тематическом плане, которая представляет собой совокупность, объединённую общей целью, содержанием, организационными формами, образующими некоторую целостность.

Средний коэффициент усвоения, подсчитанный по тем же методикам, которые использовались в начале опытно-экспериментальной работы, показал положительную динамику коэффициента усвоения.

Таблица 2.3

Контрольный срез определения уровня сформированности
логического мышления экспериментального класса

№ П/П	Список учащихся	Задания						Коэффициент Усвоения
		1	2	3	4	5	6
1	Арслан	+	+	+	+	+	+	1
2	Нурзиля	+	+	+	+	+	+	1
3	Айдар	+	+	+	-	-	+	0,6
4	Диана	+	+	+	+	+	+	0,6
5	Данил	+	+	-	+	-	+	0,6
6	Алина	+	-	-	+	+	+	0,6
7	Ильнур	+	+	-	-	+	+	0,6
8	Артур	+	-	+	+	+	-	0,6
9	Камилла	+	-	+	-	+	+	0,6
10	Айназ	-	+	+	-	+	+	0,6
11	Диана	+	-	+	-	-	-	0,3
12	Алия	+	+	+	+	+	+	1
13	Айнур	+	+	+	+	+	+	1
14	Реналь	+	+	-	+	+	+	0,8
15	Евгения	+	-	+	+	-	+	0,6
16	Лиана	­+	+	+	-	+	+	0,8
17	Артур	+	-	+	+	+	-	0,6
18	Ильназ	+	+	+	+	+	+	1
19	Эвелина	+	-	+	+	+	+	0,6
20	Алсу	+	+	+	+	+	+	1
21	Денис	+	-	+	+	-	+	0,6
22	Индира	+	+	+	-	+	-	0,8
23	Тимур	+	+	+	+	+	+	1
24	Ира	+	+	+	+	+	+	1
Средний коэффициент усвоения		0,8

Таблица 2.4

Контрольный срез определения уровня сформированности
логического мышления у учащихся контрольного класса

№ П/П	Список учащихся	Задания						Коэффициент Усвоения
		1	2	3	4	5	6
1	Дмитрий	+	-	-	+	-	-	0,3
2	Иван	+	+	+	+	+	+	1
3	Аделя	+	+	+	+	-	-	0,6
4	Ольга	+	-	+	+	+	+	0,8
5	Милана	+	-	+	+	-	-	0,5
6	Элина	­-	+	+	+	+	-	0,6
7	Эвелина	­+	-	-	-	+	-	0,3
8	Сабина	­-	-	+	+	+	+	0,6
9	Рубен	­+	-	-	-	+	-	0,3
10	Карина	+	+	+	+	+	+	1
11	Арина	+	-	+	+	+	+	0,8
12	Валерия	+	+	+	+	+	+	1
13	Савелий	+	+	+	+	+	+	1
14	Екатерина	+	-	+	+	-	+	0,6
15	Екатерина	+	-	+	+	+	+	0,8
16	Богдан	+	+	+	+	+	+	1
17	Саша	+	-	+	+	-	-	0,5
18	Александр	+	+	_	+	+	+	0,8
19	Искандар	­-	-	+	-	+	-	0,3
20	Валерия	+	-	+	-	-	+	0,3
21	Карина	+	+	+	+	+	-	0,6
22	Алина	­+	-	-	-	+	-	0,3
23	Денис	+	-	-	+	-	+	0,5
24	Рубен	+	-	-	+	-	+	0,5
Средний коэффициент усвоения		0,71

Таблица 2.5

Сравнительная таблица коэффициента усвоения логического мышления
младших школьников экспериментального и контрольного классов

Этап эксперимента	Средний коэффициент усвоения
	ЭК	КК
Констатирующий	0,64	0,63
Контрольный	0,8	0,71
Динамика	0,16	0,08

Сравнивая результаты исследований, мы отмечаем значительные изменения. У большинства учащихся экспериментального класса средний коэффициент усвоения повысился на 0,16%. Но в контрольном классе эти изменения незначительны (изменение лишь на 0,08%), так как не проводилась систематическая работа по формированию логического мышления у учащихся этого класса. Разница составила 0,16-0,08=0,08%.

Рис. 2.1. Динамика коэффициента усвоения логического мышления младших школьников экспериментального и контрольного классов.

На рисунке 2.1 под номером « 1»показана динамика коэффициента усвоения логического мышления в экспериментальном классе и под номером «2», динамика коэффициента усвоения логического мышления в контрольном классе. Положительная динамика коэффициента усвоения в экспериментальном классе позволила сделать вывод о подтверждении гипотезы исследования. Значит, если на уроках математики реализованы следующие условия:

– систематически используются специальные задачи и задания, направленные на развитие логического мышления;

– решаются «трудные задачи» с необычным условием, в которых предоставляется возможность порассуждать;

– выполняется логическое и осознанное исследование реального мира, то уровень развития логического мышления младших школьников повысится.

К данной главе выводы мы формулируем следующим образом.

Для формирования логического мышления необходимо развивать познавательную активность учащихся. Важнейшим моментом, влияющим на развитие познавательной активности, является интерес к деятельности, наличие мотивации.

Задачи формирования логического мышления решаются при изучении математического материала. Изучение материала способствует формированию пространственных и плоскостных представлений детей, прививает элементарные навыки определения простейших математических понятий, навыки чёткой формулировки выводов на основе наблюдений. В процессе накопления математических представлений основную роль играют наблюдения и практическая деятельность обучающихся. Прием это отдельные операции, умственные или практические действия педагога или детей, которые дополняют форму усвоения материала. Умственные действия – действия человека, выполняемые во внутреннем плане сознания, без опоры на внешние средства, в том числе слышимую речь. Приёмы умственных действий – сравнение, обобщение, анализ, синтез, классификация, систематизация – в литературе также называют логическими приемами мышления. Ведущими приемами умственных действий является анализ, синтез, сравнение.

Логическая составляющая начального математического образования связана с развитием мышления учащихся, привитием ему умений строить умозаключения, выполнять логические операции сравнения, сопоставления, доказательства, непротиворечиво давать определения понятиям.

Умение четко, последовательно излагать свои мысли, тесно связано с умением представлять сложное действие в виде организованной последовательности простых.

Младшие школьники постоянно осваивают на уроках правила, сформулированные в виде алгоритмических предписаний. Важно, на занятиях посвященных формированию логического мышления все внимание учащихся концентрировать на построении алгоритма. При этом важно на занятиях посвященных формированию логического мышления у младших школьников, действуя с конкретными объектами и обобщениями в виде правил, овладевать умением выделять элементарные шаги своих действий и определять их последовательность. Рассмотрены основные методы и приёмы, направленные на формирование логического мышления младших школьников на уроках математики. Для проверки эффективности созданных нами условий развития логического мышления младших школьников на уроках математики был проведен педагогической эксперимент.

Результаты показали, что специально подобранные упражнения для младших школьников действительно способствуют формированию приемов умственных действий. Разработанные и апробируемые на практике задания способствуют:

– формированию приемов умственных действий (анализ, синтез, сравнение);

– формированию логического мышления младших школьников на уроках математики;

– снижению количества ошибок при выполнении заданий.

Для достоверности теоретических предположений и обработки экспериментальных данных, подтверждающих гипотезу исследования, проведена статистическая обработка результатов.

ЗАКЛЮЧЕНИЕ

Младший школьный возраст является активным пропедевтическим этапом развития логического и алгоритмического мышления, в ходе которого закладываются основы осуществления логических операций синтеза, анализа, обобщения, аналогии, классификации, сравнения, абстрагирования и других, которые являются базой успешного овладения учебной программой общеобразовательной школы.

В представленной выпускной квалификационной работе поставлены и решены следующие задачи:

– уточнено понятие «логическое мышление младших школьников» на основе изучения и анализа педагогической и методической литературы;

– описана система работы над формированием логического мышления младших школьников на уроках математики;

– экспериментально проверена система работы над формированием логического мышления на уроках математики.

– сформулированы рекомендации по формированию логического мышления младших школьников для учителей начальных классов.

При решении первой задачи были изучены теоретические основы формирования логического мышления у младших школьников в процессе обучении математике. Логическое мышление изучалось учеными Е.В. Веселовской, Е.Е. Останиной, А.А. Столяр, Л.М. Фридман, М.Н. Шардаковым, который в 1963 г. опубликовал книгу «Мышление школьника». В начальном курсе математики они представлены в трудах Ш.А. Амонашвили, А.В. Белошистой, В.В. Давыдова, Н.Б. Истоминой, М. Монтессори.

При решении второй задачи исследования обоснована специфика построения системы заданий, необходимых для развития логического мышления у младших школьников.

Решением третьей задачи является проведение опытно-экспериментальной работы на базе казённого государственного учреждения «Общеобразовательная средняя школа №10 г. Актау Республики Казахстан» в течение первой и второй четверти. Были выбраны два класса: 3«Г» – экспериментальный класс и 3 «Ж» – контрольный класс.

На констатирующем этапе был установлен коэффициент усвоения, который выявил состояние формирования логического мышления у младших школьников. В ЭК коэффициент усвоения равен 0,64%, а в КК коэффициент усвоения равен 0,63%. Во время формирующего эксперимента на уроках математики использовались разные задания для формирования логического и алгоритмического мышления. Контрольный срез показал, что коэффициент усвоения после проведения формирующего эксперимента в экспериментальном классе на 0,08 % больше, чем в контрольном классе.

Цель работы, заключающаяся в том, чтобы дополнить систему заданий курса математики третьего класса, направленной на формирование логического мышления, специальными заданиями необходимыми для успешного решения практических задач и продолжения обучения достигнута. Проведенное опытно-экспериментальное исследование показало наличие положительной динамики в развитии логического и алгоритмического мышления у младших школьников.

Гипотеза исследования о том, что коэффициент усвоения приемов сформированности логического мышления у младших школьников в процессе обучения математике повысится, если применять специальные логические задания и упражнения, подтверждена.

Полученные результаты исследования позволили сформулировать методические рекомендации по развитию логического мышления младших школьников.

– необходимо уделять должное внимание формированию логического мышления не только в первом и втором классах, но и третьем классе;

– для формирования логического мышления, урок математики целесообразно начинать с выполнения «математической гимнастики» или «логической пятиминутки»;

– логическое мышление можно формировать не только на специальных заданиях предложенных в учебниках, но и на дополнительных заданиях из других источников информации;

– формирование логического мышления можно продолжить вне урока: участие в олимпиадах, в математических мероприятиях, в различных математических конкурсах и викторинах конкурса.

Считаем, что цель работы достигнута, задачи, поставленные в ней, выполнены.

СПИСОК Использованных источников и литературы

1. Абдуллина Л.Б., Мустафина Р.З., Шмелева Н.Г. Избранные вопросы теории и технологии обучения математике: в двух частях Учеб.-метод. материалы для студентов 1-5 курсов по специальности « 050708 – Педагогика и методика начального образования». – Стерлитамак: Стерлитамак. гос. пед. академия им. Зайнаб Биишевой, 2013. – 148 с.

2. Аргинская И.И. Математика: Методическое пособие для учителя. – М.: Учебная литература, 1995. – 132с.

3. Аргинская И.И. Методическое пособие к учебнику «Математика». 3 класс. – Самара: Учебная литература, 2002.– 160 с.

4. Аргинская И.И., Ивановская Е.И. Математика: Учебник для 3 класса четырехлетней начальной школы. – Самара: Учебная литература, 2002.– 192 с.

5. Аргинская И.И., Ивановская Е.И. Математика: Учебник для 4 класса. – 2-е издание, исправленное. – Самара: Учебная литература, 2002. –192 с.

6. Белошистая А.В., Левитес В.В. Развитие логического и алгоритмического мышление младшего школьника // Начальная школа плюс До и После. – 2006. – №9. – С. 35-39 .

7. Белошистая А.В., Левитес В.В. Тетрадь для развития логического и алгоритмического мышления в 1-м классе. – М.: Классик-Стиль, 2005. – 34 с.

8. Гребенникова Н.Л. Методика обучения младших школьников математике, учебно-методический комплекс для студентов III-IV курсов по специальности «050708 – Педагогика и методика начального образования». – Стерлитамак: Стерлитамак. гос. пед. академия, 2006. – 382 с.

9. Гребенникова Н.Л., Косцова С.А. История развития методики начального математического образования. – Уфа: РИЦ БашГУ – 2012. – 186 с.

10. Гребенникова Н.Л., Косцова С.А. Теория и практика организации обучения математике в начальных классах. – Уфа: РИЦ БашГУ, 2012. – 189 с.

11. Давыдов В.В. Теория развивающего обучения. – М.: ИНТОР, 2014. – 544 с.

12. Демидова Т. Е, Козлова С.А., Тонких А.П. Моя математика: Учебник для 1-4 классов.– М.: Баласс, 2005. – 245 с.

13. Демидова Т.Е, Козлова С.А., Рубин А.Г., Тонких А.П. Содержательная линия «Занимательные и нестандартные задачи» в учебниках «Моя математика» // Начальная школа плюс До и После. – 2005. – №9. – С. 38-42.

14. Истомина Н.Б. Математика. 1 класс: Учебник для четырёхлетней начальной школы. – Смоленск: Ассоциация XXI век, 2014. – 176 с.

15. Истомина Н.Б. Математика. 2 класс: Учебник для четырёхлетней начальной школы. – Смоленск: Ассоциация XXI век, 2000. – 176 с.

16. Истомина Н.Б. Математика. 3 класс: Учебник для четырёхлетней начальной школы. – Смоленск: Ассоциация XXI век, 2000. – 176 с.

17. Истомина Н.Б. Математика. 4 класс: Учебник для четырёхлетней начальной школы. – Смоленск: Ассоциация XXI век, 2000. – 240 с.

18. Истомина Н.Б. Методика обучения математике в начальной школе. – М.: Академия, 2015. – 365 с.

19. Канбекова Р.В Мангитбаева Л.В. Развитие мышления младших школьников // Интеграция психолого-педагогической теории и практики в поликультурном образовательном пространстве Поволжья и Урала: Сб. науч. трудов по материалам IV Всерос. заоч. науч. конф. 25 мая 2016г, г. Стерлитамак. – Стерлитамак. 2016. С. 132-135.

20. Канбекова Р.В. Математика; учебно–методический комплекс для бакалавров по направлению подготовки « 050100 – Педагогическое образование. Профиль: Начальное образование» – Уфа: БашГУ; Стерлитамак. гос. пед. академия им. Зайнаб Биишевой, 2012. – 208 с.

21. Канбекова Р.В. Модель профессиональной подготовки будущего педагога в дидактической системе с элементами открытого образования: Монография. – Стерлитамак: Стерлитамакский филиал БашГУ, 2013. – 208 с.

22. Канбекова Р.В. Формируем информационную компетентность образовательно-инновационные технологии: теория и практика: коллективная монография / Под общей ред. проф. О.И. Кирикова. Книга 19. – М.: Наука: Информ; Воронеж: ВГПУ, 2014. – Глава II. – С. 18-33.

23. Канбекова Р.В., Мангитбаева Л.В. Рекомендации по реализации здоровьесберегающей функции педагога на уроках математике // Начальное образование. – 2016 – №6. – С. 55-61.

24. Козлова С.А. Развитие логического и алгоритмического мышления у дошкольников и младших школьников // Начальная школа плюс До и После. –2006. – №9. – С. 18-25.

25. Кондаков Н.И. Логический словарь. – М.: Академия, 2013. – 540 с.

26. Локк Дж. Опыт о человеческом разумении: В 3 т. – Т. 1. – М.: Наука, 1988. – 171 с.

27. Мельник Н.В. Развитие логического мышления при изучении математики // Начальная школа. – 2014. – №5. – С. 54-61.

28. Моро М. И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С. В. Математика: Учебник для 4 класса четырёхлетней начальной школы. В 2 частях.– М.: Просвещение, АО «Московские учебники», 2014. – 112 с.

29. Моро М.И., Бантова М.А., Бельтюкова Г. В., Волкова С.И., Степанова С. В. Математика: Учебник для 2 класса начальной школы. В 2 частях. Часть 2.– М.: Просвещение, АО «Московские учебники», 2014. – 96 с.

30. Моро М.И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С. В. Математика: Учебник для 2 класса начальной школы. В 2 частях. – Часть 1. – М.: Просвещение, АО «Московские учебники», 2014. – 80 с.

31. Моро М.И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С. В. Математика: Учебник для 4 класса четырёхлетней начальной школы. В 2 частях. Часть 2. Второе издание. – М.: Просвещение, АО «Московские учебники», 2014. – 112 с.

32. Моро М.И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С. В. Математика: Учебник для 3 класса четырёхлетней начальной школы. В 2 частях. Часть 2. – М.: Просвещение, «Московские учебники», 2014. – 140 с.

33. Моро М.И., Волкова С.И., Степанова С.В. Математика: Учебник для 1 класса начальной школы. В 2 частях. Часть 1. Второе издание. – М.: Просвещение, АО «Московские учебники», 2014. – 112 с.

34. Мустафина Р.З. Развитие речи при обучении младших школьников математике // Башкортостан уkытыусыhы. – 2012. №10. – С. 32-34.

35. Мустафина Р.З. Требования к проведению дидактических игр // Башкортостан уkытыусыhы. – 2012. – №2. – С. 26-28.

36. Немов Р.С. Психология: в 3-х кн. – М.: Просвещение, 2002. – 304 с.

37. Оспанов Т.К. , Курманалина Ш.К., Кайынбаев Ж.Т. Математика для 2 класса общеобразоват. шк. – 4-е изд., перераб. – Алматы: Атамура, 2013 – 272с.

38. Оспанов Т.К., Косанов Б.М., Кайынбаев Ж.Т. Математика: Учебник для 3 класса общеобразовательной школы. В 2 частях. – Часть 1. – Алматы: Атамура, 2013 – 272 с.

39. Петерсон Л.Г. Математика. 1 класс. Часть 1. – М.: Просвещение, 2002.– 480 с.

40. Рубинштейн С.Л. Бытие и сознание. – М.: Просвещение, 2002. – 256 с.

41. Рубцов В.В. Проектирование развивающей образовательной среды школы. – М.: МГППУ, 2002. – 272 с.

42. Стойлова Л.П. Математика. – М.: Академия, 2002. – 480 с.

43. Сухина И.Г. 800 новых логических и математических головоломок. – М.: СПб Союз, 2004. – 208 с.

44. Талызина, Н.Ф. Педагогическая психология : учеб. для студ. сред. учеб. зав. – М.: Академия, 2006 – 340 с.

45. Тихоненко А.В., Русинова М.М., Налесесная С.Л., Трофименко Ю.В. Теоретические и методические основы в изучении математики в начальной школе. – Р. н/Д.: Книга, 2008. – 540 с.

46. Ульяницкая Т.В. Развитие логического мышления младших школьников на уроке математики // Начальная школа плюс До и После. – 2012. – №12. – С. 35-41.

47. Фридман Л.М. Психология детей и подростков. – М.: Издательство Института Психотерапии, 2004. – 480 с.

48. Холодова О.А. // Умникам и умницам: Курс по развитию познавательных способностей. Метод. пос. для 3 кл. – Изд. 3-е, исправленное. – М.: РОСТ, 2014. – С. 15-18.

49. Холодова О.А. // Умникам и умницам: Курс по развитию познавательных способностей. Метод. пос. для 2 кл. – Изд.3-е, исправленное. – М: РОСТ, 2014. – С. 20-21.

50. Шардаков М.Н. Мышление школьника. – М.: Просвещение, 2000. – 540 с.

51. Шмелева Н.Г Инновационная деятельность педагога в системе современного образования // Образование в пространстве школы и вуза: опыт, проблемы, перспективы: Сб. материалов II Междунар. науч.-практ. конф. 27 ноября 2013 г, г. Стерлитамак. – Стерлитамакский филиал БашГУ. 2013. – С. 286-201.

52. Шмелева Н.Г. О применении интегрального представления при решении краевых задач // Прикладная физика и математика. – 2014. – №2. – С. 57-67.

53. Эльконин Д.Б. Психология обучения младшего школьника. – М.: Просвещение, 2001. – 264 с.

Приложение№1

Календарно-тематическое планирование уроков по математике
для 3 класса

№ п/п	Наименование раздела программы		Кол-во часов		Тип урока		Дата	Вид контроля			Цели и задачи		Требования к уровню подготовленности уч-ся
													Знать	Уметь
1 ЧЕТВЕРТЬ
		ПОВТОРЕНИЕ	14 ЧАСОВ								Уточнить знания нумерации чисел в пределах100.Повторить приемы сложения и вычитания, переместительный закон. Развивать вычислительные навыки ,логичесое мышление, умение решать задачи. Познакомить с латинскими буквами в выражениях. Закреплять навыки решения уравнений.Совершенствовать умение чертитьи измерять отрезки , стороить геометрические фигуры. Развивать умения рассуждать,анализировать, логически мыслить.		Названияи последовательностьчисел в пределах 100названия компонентов и результатовсложенияи вычитания,таблицу сложения и соответствующие случаи вычитания, знать названия и признаки геометрических фигур.	Читать,записывать,сравнивать числа в пределах100. Находить сумму и разность чисел в пределах 100.Чертить геометрические фигурыи находить их периметр.Решать уравнения и числовые выраженияв 2 действия.
1.		Табличное сложение и вычитание в пределах 20	1		З		05.09.16	Текущ.
2.		Устное и письменное сложение и вычитание с переходом через десяток в пределах100.	1		З		06.09.16	Тек.,фронт.,инд..
3.		Чтение,запись,сравнение натуральных чисел впределах 1000	1		Н		08.09.16	Текущ,групповая
4.		Устные приемы сложения и вычитания.Правила порядка выполнения действий сложения и вычитания	1		Н		09.09.16	Текущ.
5.		Взаимосвязь сложения и вычитания.Правила порядка выполнения действия сложенияи вычитания.	1		ПЗ		12.09.16	Текущ,фронт,парн.
6.		Сравнение величин таких как: длина,масса,время,вместимостимость.Действия с величинами.	1		Н		13.09.16	текущ.тнд.
7.		Составлениеи решение уравнений.	1		Н		19.09.16	Текущ,груп.
8-9		Табличные случаи умножения и деления на 2,3,4.	2		З		20.09.16.	Текущ.,фронт.
10.		Контрольная работа №1	1		К		22.09.16	Индив.
11..		Составление числовых и буквенных выраженийнахождение их значения.Равенство.Неравенство.	1		З		23.09.16.	Тематич.
12.		Составление и решение задач в одно действие	1		Н		26.09.16	Текущ.
13.-14		Распознавание геометрических фигур.Периметр многоугольника.	2 2		З		27.09.1628.09.16	Текущ.фронт,групповая
		П
		УМНОЖЕНИЕ ОДНОЗНАЧНЫХ ЧИСЕЛ И СООТВЕТСТВУЮЩИЕ СЛУЧАИ ДЕЛЕНИЯ. ПЛОЩАДЬ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ. БУКВЕННОЕ ВЫРАЖЕНИЕ. УРАВНЕНИЕ.									Повторить смысл умножения.Закрепить умения рассуждать,решать задачи,анализироватьи мыслить логически Закрепить знания о связи между компонентамии результатом умножения.Дать понятие четные и нечетные числа.Совершенствовать вычислительные навыки и умения решать текстовые задачи свеличинами:цена,количество,стоимость; на увеличениеи уменьшение числанесколько раз.		Таблицу умножения и соответствующие случаи деления, правила выполнения действий в выражениях в 2-3 действия(со скобками и без них).Знать термины: цена,количество,стоимость.	Вычислять значения числовых выражений,содержащих 2-3 действия(со скобками и без них).,опираясь на знание таблицы умножения. Уметь составлять и решать уравнения.Вычеслять площадь прямоугольника.Решатьпростые и составные задачи.Уметь последовательно рассуждатьи сравнивать
15		Умножение.Деление.Переместительное свойство умножения.Повторение.	1	Н		30.09.16			Текущ..фронтальн,тндивид.
16		Задачи на умножение и деление в одно действие.	1	З		03.10.16.			Текущ.
17		Сравнение площадей фигур.	1	З		04.10.16			Текущ,парн.
18		Умножение чисел на 0 и на 1.	1	Н		06.10.16.			Текущ,индив.
19		Числовые, выражения содержащие одно действие	1	З		07.10.16.			Текущ,парн.
20		Правила нахождения неизвестных компонентов умножения	1	Н		10.10.16			Текущ.коллект,письмен.

ПРИЛОЖЕНИЕ№2

Конспект урока на тему «Составление и решение задач
в одно и два действия»

Цель: познакомить учащихся с решением задач в два действия составлением выражения и их письменным объяснением; формирование логическое мышление при решении задач, умения и навыков устного объяснения решения задач в два действия способом составления выражения; познакомить с единицами измерения времени – часом и минутой; развивать математическую речь, внимание, память. Прививать любовь к предмету.

Оборудование: геометрические фигуры, сигнальные карточки, карточки для индивидуальной работы, для работы в парах, в группах, компьютер, презентация.

Ход урока.

І. Организационный момент.

Сначала сядут ребята, у которых лежит фигура с прямыми углами. Затем с острыми углами, а теперь с тупыми углами. Эти фигуры вам понадобятся для работы в группах.

ІІ. Актуализация знаний учащихся.

1. Ожидание.

Что вы ожидаете от урока? Я ожидаю, что вы будете активными и творческими. Работать будем под девизом: слайд №2.

Думай – быстро

Отвечай – точно

Решай – правильно

1. Графический диктант «Кот».

Начнем наш урок с графического диктанта. Будьте внимательны, и гость нашего урока появится на страничке вашей тетради.

Диктант: от начальной точки одна клетка вправо, одна клетка вниз, две вправо, одна вверх, одна вправо, две вниз, пять вправо, две вверх, одна влево, одна вверх, две вправо, восемь вниз, одна влево, две вверх, одна влево, две вниз, одна влево, две вверх, три влево, две вниз, одна влево, две вверх, одна влево, две вниз, одна влево, три вверх, одна влево, четыре вверх, соединяем в начальной точке.

3. Расставьте в порядке возрастания числа и узнаете его имя.

Слайд №3.

23 30 45 52 60 74 91

В А С И Л И Й

Назовите число 5-го десятка, 8-го десятка, назовите его соседей.

4. Индивидуальная работа по карточкам.

Кот Василий предлагает поработать по карточкам и распутать клубок.

Соедини с правильным ответом

80 + 5= 30 59 + 1 = 96

90 + 6 = 39 40 – 1 = 85

47 – 40 = 60 38 – 8 = 7

5.Выполнение логических заданий:

Игра «Наоборот»

Сумма – разность, день – ночь, час – минута, метр – см, однозначное –двузначное, простая – составная.

Этими терминами мы будем пользоваться на уроке.

6. «Незаконченное предложение».

Закончить предложения. Слайд №4.

От перестановки слагаемых….

Результат при сложении…

Что имеет условие, вопрос, решение, ответ….

7. Устный счет

а) Игра « Истина – ложь»

Проверим навыки устного счета. Если с высказыванием согласны подымите карточку зеленого цвета, если нет красного.

– сумма чисел 50 и 9 равна 49

– разность чисел 27 и 7 равна 20

60 увеличить на 7 будет 47

От 45 отнять 5 будет 40

б) Прочитать разными способами примеры и вычислить их. Слайд №5.

68-8= 60 37 + 1=38

Соотнесите ответы с темой «Коты»

60 м – расстояние, на которое могут видеть кошки

38 градусов – температура тела кошки.

8. Что изменилось? (Сравните следующие признаки: цвет, форма, размер)

9. Минутка каллиграфии.

Запишите цифры 1, 3, 5. Слайд №6.

Образуйте все возможные двузначные числа. Подчеркните количество десятков.

Сколько чисел образовали? (9).

9. Разложить на сумму разрядных слагаемых числа.

1-ряд. с одинаковым количеством десятков и единиц

2-ряд. Числа, где количество единиц меньше количества десятков

3-ряд. Числа, где количество десятков меньше количества единиц

Проверка. Зачитывают д/в. Охарактеризуйте число 15.Свяжите с темой «Коты» (средний срок жизни).

ІІІ. Сообщение темы и цели урока. Мотивация учебной деятельности.

1. Подготовительная работа.

В первой корзине 3 котенка, во второй 4, а в третьей-5.

Что узнаем, выполнив действие 4+3, 5-3, 7+5

Составьте выражение, с помощью которого можно узнать, сколько котят в трех корзинах.

Сегодня мы научимся решать задачи составлением выражения.

Физкультминутка (под музыку)

ІV. Изучение нового материала.

1. Решение задачи.

Было – 90 к.

Израсходовал – 50 к. и 30 к.

Осталось – ?

Какие числа нужно вписать в окошечки?

Что узнаем, вычислив результат?

Было 90 к., а израсходовали (50+30). Что можно узнать?

– какое выражение можно составить?

– запишите выражение: 90-(50+30)

2. Первичное закрепление задача №5

V. Развитие математических знаний

1. Работа в парах.

Нахождение буквенных выражений (карточки)

1-я. а +20, 80 –а, если а=40

2-я. а +20, 80 –а, если а =20

3-я. а +20, 80 –а, если а =30

1. Ознакомление с единицами измерения времени

Назовите знакомые вам единицы измерения длины; единицы измерения веса.

Кто знает, чем измеряется время?

Минута – непродолжительный промежуток времени. О какой-нибудь легкой работе, говорят: «Минутное дело»

Для врачей – это спасенная жизнь. Для ученых – открытие нового, да и пожарные, и саперы совсем по-другому относятся к минутам. Минуты бегут друг за другом, а догнать их или вернуть нельзя.

1 ч = 60 мин, 1 сут.= 24 ч.

1. Работа в группах

Объединиться в группы за фигурами

Решить, применяя переместительное свойство действия сложения

1гр. 4 + 30 +5 +40 80 + 6 + 10

2гр. 50 + 2 + 30 + 6 20 + 7 + 50

3гр. 30 + 1 + 60 + 6 80 + 6 + 10

1. Выполнение задачи №338 самостоятельно, записав выражением

VI. Итог урока. Рефлексия. Слайд №12.

Я узнал(а)…

Я научился(ась)…

Мне понравилось…

VII. Домашнее задание – С.25, №№9,11.