Вычисление интегралов

Математику уж затем изучать нужно, что она ум в порядок приводит… Ломоносов

Методы интегрирования

( комбинированный урок)

Вычисление интеграла непосредственным интегрированием:

• По свойствам интегралов:

Вычисление интеграла непосредственным интегрированием:

Вычисление интеграла методом подстановки:

• Главное, правильно ввести подстановку!

t

Вычисление интеграла методом подстановки:

• Проверка домашнего задания

• Интегрирование подстановкой ( замена переменной ).
• Интегрирование по частям .

Интегрирование по частям

• Интегрированием по частям называется нахождение интеграла по формуле

Где u и v – непрерывно дифференцируемые функции от x . Отыскание интеграла сводится к нахождению более простого интеграла. При этом в качестве u берется функция, которая при дифференцировании упрощается, а в качестве dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Скажи мне, и я забуду. Покажи мне, и я запомню. Дай мне действовать самому и я научусь! Конфуций

• Проверка домашнего задания
• Обзор методов интегрирования

• Вычислить интегралы:

u

dv

Интегрирование по ч а с т я м

u

dv

• Вычислить интегралы:

dv

u

u

dv

dv

.

.

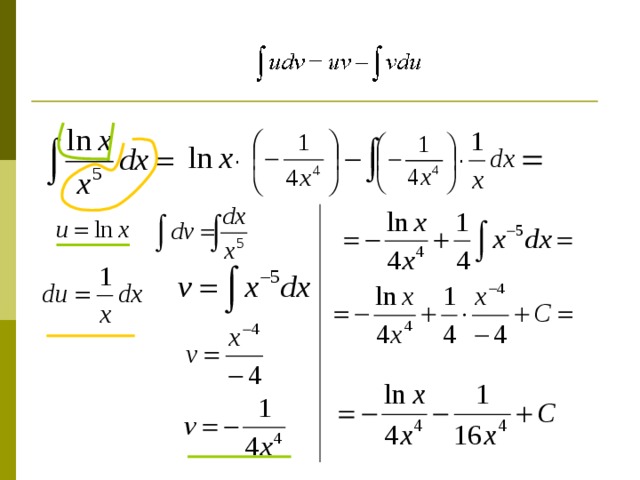
• Проверка домашнего задания
• Обзор методов интегрирования
• Практические навыки

• Проверка домашнего задания
• Обзор методов интегрирования
• Практические навыки
• Играем

• Проверка домашнего задания
• Обзор методов интегрирования
• Практические навыки
• Играем
• Решаем самостоятельно

Удачного дня!