Получите свидетельство
Вход
Треугольник – самая простая замкнутая
геометрическая фигура, одна из первых,
свойства которой человек узнал ещё в
глубокой древности В одном египетском папирусе 4000-летней давности говорилось о площади равнобедренного треугольника. Через 2000 лет в Древней Греции очень активно велось изучение его свойств. Император Франции Наполеон свободное время посвящал занятиям математикой и, в частности, изучению свойств треугольников. Большой вклад в исследование треугольников внес знаменитый математик …,
имя которого мы назовём, ответив на следующие вопросы
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
2
2
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
3
3
Биссектриса треугольника – луч, делящий угол на два равных угла ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
4
4
Отрезок биссектрисы угла, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
5
5
Медианы треугольника пересекаются
в одной точке, и точка пересечения всегда лежит внутри треугольника ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
6
6
Из точки, не лежащей на прямой, можно провести, по крайней мере, два перпендикуляра к ней ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
7
7
Две прямые называются перпендикулярными,
если при их пересечении образуется хотя бы один
прямой угол
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
8
8
Сумма углов треугольника равна двести градусов. ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
9
9
Три стороны треугольника пересекаются в одной точке,
и она всегда лежит внутри треугольника ;
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
10
10
Три биссектрисы треугольника пересекаются в одной точке,
и эта точка лежит внутри треугольника .
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
11
11
Древнегреческий математик.
Дата рождения :
ок. 325 года до н.э.
Научная сфера:
математика
Известен как:
«Отец Геометрии»
Из дошедших до нас сочинений Евклида наиболее знамениты «Начала»,
состоящие из 15 книг.
В 1-й книге изучаются свойства треугольников
12
12
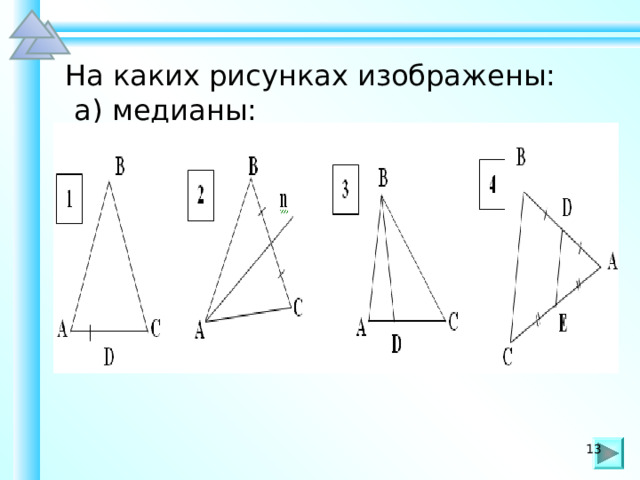
На каких рисунках изображены:
а) медианы:
13
13
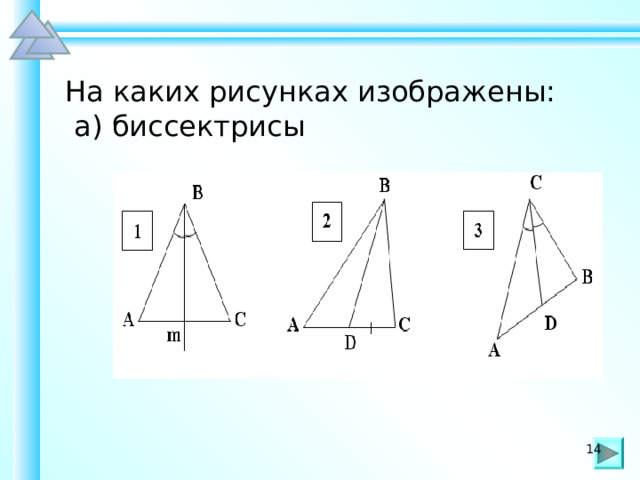
На каких рисунках изображены:
а) биссектрисы
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
14
14
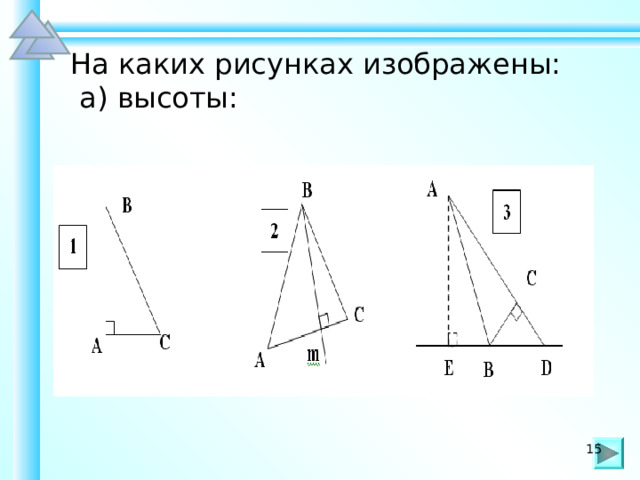
На каких рисунках изображены:
а) высоты:
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
15
15
Урок геометрии, 7 класс
Шаблон для создания презентаций к урокам математики. Савченко Е.М.
16
16
http://files.school-collection.edu.ru/dlrstore/7383a655-0dac-11dc-8314-0800200c9a66/index.htm
http://files.school-collection.edu.ru/dlrstore/7383a654-0dac-11dc-8314-0800200c9a66/index.htm
17
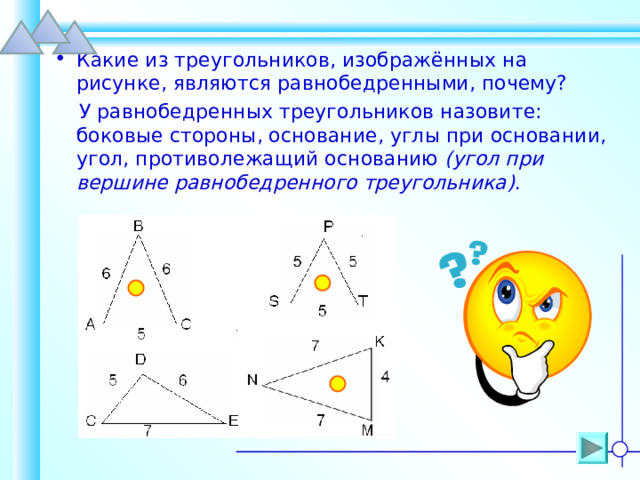
- Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему?
У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника) .
Свойства равнобедренного треугольника
A
B
C
A
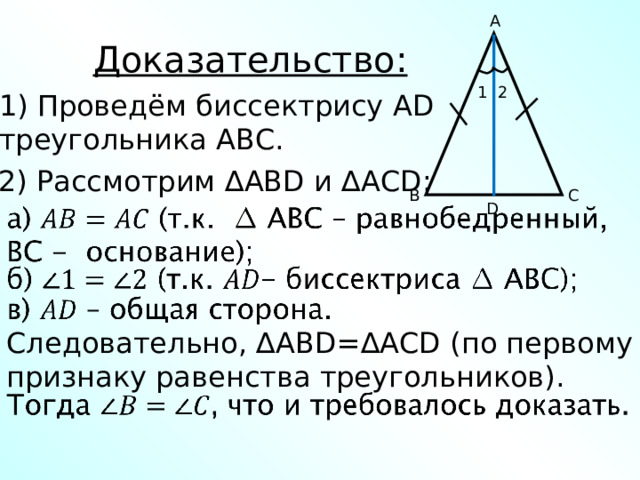
Доказательство:
1
2
1) Проведём биссектрису AD треугольника АВС.
2) Рассмотрим ∆ ABD и ∆ ACD :
C
B
D
Следовательно, ∆ ABD =∆ ACD (по первому признаку равенства треугольников).
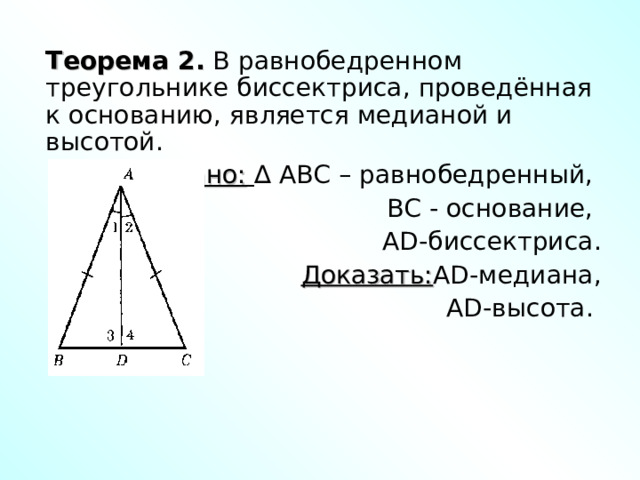
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Дано: ∆ ABC – равнобедренный,
ВС - основание,
AD -биссектриса.
Доказать: AD -медиана,
AD -высота.
Доказательство:
1) Рассмотрим ∆ ABD и ∆ ACD :
Следовательно, ∆ ABD =∆ ACD (по первому признаку равенства треугольников).
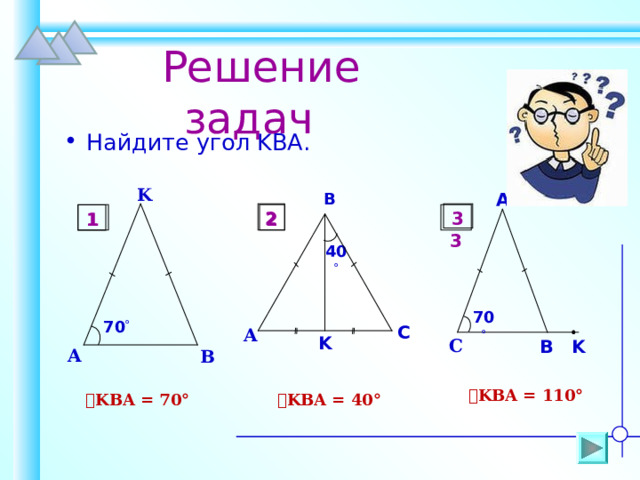
Решение задач
- Найдите угол KBA .
K
B
A
2
3
3
2
1
1
40
70
70
C
A
K
C
K
B
A
B
ے KBA = 110°
ے KBA = 40°
ے KBA = 70°
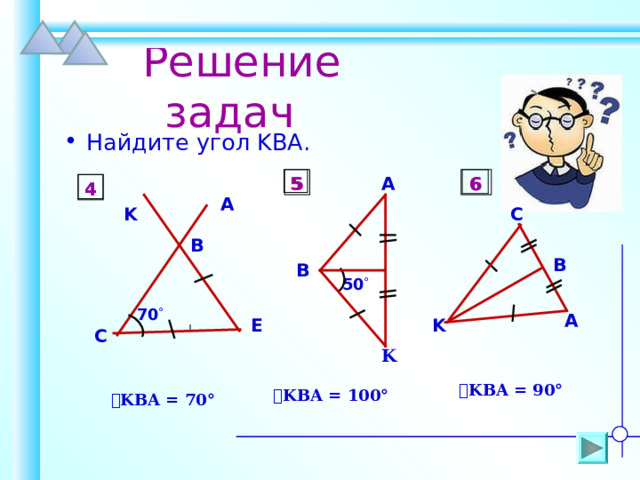
Решение задач
- Найдите угол KBA .
6
5
5
6
A
4
4
A
K
C
B
B
B
50
70
A
E
K
C
K
ے KBA = 90°
ے KBA = 10 0°
ے KBA = 70°
Решение задач
- В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите периметр треугольника.
- В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.
- В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.
- В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.
26
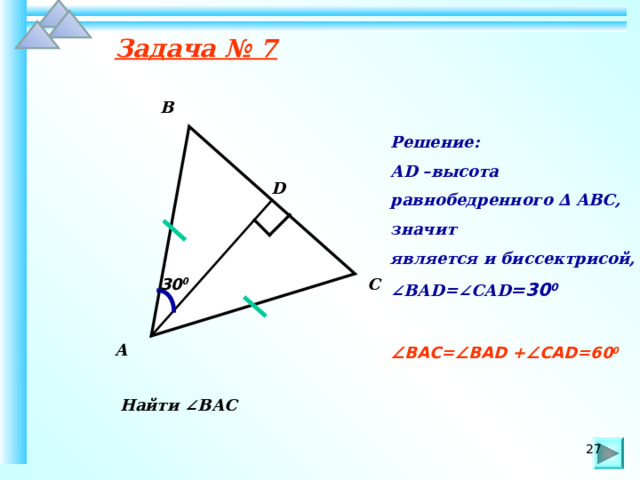
Задача № 7
В
Решение:
А D –высота
равнобедренного ∆ АВС,
значит
является и биссектрисой,
∠ ВА D =∠СА D =30 0
∠ ВАС=∠ВА D +∠СА D =60 0
D
С
30 0
А
Найти ∠ВАС
27
Контрольные вопросы
- Какой треугольник называется равнобедренным?
- Какой треугольник называется равносторонним?
- Является ли равносторонний треугольник равнобедренным?
- Каким свойством обладают углы
в равнобедренном треугольнике?
- Каким свойством обладает биссектриса, проведённая к основанию равнобедренного треугольника?
Домашнее задание
- Изучить п. 18
- Выполнить №108 на стр. 37.
- Достройте треугольник своего настроения
- Достройте треугольник своего настроения
- Достройте треугольник своего настроения
- Достройте треугольник своего настроения
30
Второй признак равенства треугольников. (2.61 MB)
0
415
22
Нравится
0
